
|
|
Средние величины для анализа рядов динамикиВзвешенные
ряду распределения
Ряд мажорантности средних:
Средняя хронологическая(используется для расчета средних значений моментных рядов динамики)
|
ПРАВИЛА СЛОЖЕНИЯ ДИСПЕРСИИ
1) Общая дисперсия – характеризует вариацию всех единиц совокупности от общей средней.
 2) Частная (внутригрупповая)
2) Частная (внутригрупповая)  –характеризуют вариацию признака в группах от групповой средней.
3) Межгрупповая дисперсия –характеризуют вариацию признака в группах от групповой средней.
3) Межгрупповая дисперсия  - характеризует вариацию межгрупповых средних от общей средней.
Коэффициент детерминации – показывает долю общей вариации результативного признака, обусловленную вариацией группировочного признака. - характеризует вариацию межгрупповых средних от общей средней.
Коэффициент детерминации – показывает долю общей вариации результативного признака, обусловленную вариацией группировочного признака.
 Эмпирическое корреляционное отношение
Эмпирическое корреляционное отношение
 , ,  , Если , Если  , то группировочный признак не оказывает влияния на результативный. Если , то группировочный признак не оказывает влияния на результативный. Если  , то изменение результативного признака полностью обусловлено группировочным признаком, т.е. между ними существует функциональная связь.
РЯДЫ ДИНАМИКИ
Характеризуют изменение уровня показателя во времени. Подразделяются на ряды динамики абсолютных, средних и относительных величин.
Аналитические показатели для анализа рядов динамики , то изменение результативного признака полностью обусловлено группировочным признаком, т.е. между ними существует функциональная связь.
РЯДЫ ДИНАМИКИ
Характеризуют изменение уровня показателя во времени. Подразделяются на ряды динамики абсолютных, средних и относительных величин.
Аналитические показатели для анализа рядов динамики
 Абсолютный базисный прирост Абсолютный базисный прирост
 Абсолютный цепной прирост Абсолютный цепной прирост
 Темп роста базисный Темп роста базисный
 Темп роста цепной Темп роста цепной
 Темп прироста базисный Темп прироста базисный
 Темп прироста цепной
Свойства показателей Темп прироста цепной
Свойства показателей
1. Произведение ряда последовательных цепных темпов роста (коэффициентов) = соответствующему базисному. 2. Частное от деления 2-х рядом стоящих базисных темпов роста = соответствующему цепному.
Средние величины для анализа рядов динамики 1. Ср. уровень периодического ряда динамики 2. Ср. уровень моментного ряда динамики исчисляется по формуле ср. хронологической
| 3. Средний абсолютный прирост находим по формуле ср. арифметической простой из цепных показателей
4. Средний темп роста – определяем по формуле ср. геометрической из цепных коэффициентов.
 , где n – кол-во элементов в ряду динамики
5. Средний темп прироста находится по формуле: средний темп роста – 100%(если в %) или 1 (если в коэффициентах) , где n – кол-во элементов в ряду динамики
5. Средний темп прироста находится по формуле: средний темп роста – 100%(если в %) или 1 (если в коэффициентах)
 , где Is - ИНДЕКС СЕЗОННОСТИ В РЯДАХ ДИНАМИКИ , где Is - ИНДЕКС СЕЗОННОСТИ В РЯДАХ ДИНАМИКИ
 - среднемесячный уровень ряда по одноименным месяцам - среднемесячный уровень ряда по одноименным месяцам
 - общий средний уровень ряда (постоянная средняя) - общий средний уровень ряда (постоянная средняя)
 , где Is - ИНДЕКС СЕЗОННОСТИ В РЯДАХ ДИНАМИКИ С ТЕНДЕНЦИЕЙ РАЗВИТИЯ К ПЕРЕМЕННОЙ СРЕДНЕЙ , где Is - ИНДЕКС СЕЗОННОСТИ В РЯДАХ ДИНАМИКИ С ТЕНДЕНЦИЕЙ РАЗВИТИЯ К ПЕРЕМЕННОЙ СРЕДНЕЙ
 - эмпирические уровни ряда динамики - эмпирические уровни ряда динамики
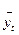 - теоретические уровни ряда динамики; n –кол-во лет
ИНДЕКСЫ
p – цена; q - кол-во; pq – выручка
i – индивидуальные индексы - теоретические уровни ряда динамики; n –кол-во лет
ИНДЕКСЫ
p – цена; q - кол-во; pq – выручка
i – индивидуальные индексы
 ; ;  ; ;  ; 0 – базисный период; 1 – отчетный период
Формулы индексов
1. Физического объема ; 0 – базисный период; 1 – отчетный период
Формулы индексов
1. Физического объема
 q - индексируемая величина
p0 - соизмеритель (вес), взятый на уровне одного и того же периода
q - индексируемая величина
p0 - соизмеритель (вес), взятый на уровне одного и того же периода
 dpq0 - это доля товарооборота отдельных видов продукции в общем товарообороте базисного периода
dpq0 - это доля товарооборота отдельных видов продукции в общем товарообороте базисного периода
 , означает абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным за счет изменения физического объема
2. Цен и других качественных показателей
Реальный индекс и среднегармонический индекс Пааше , означает абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным за счет изменения физического объема
2. Цен и других качественных показателей
Реальный индекс и среднегармонический индекс Пааше
 ; dpq1 - это доля товарооборота отдельных видов продукции в товарообороте отчетного периода ; dpq1 - это доля товарооборота отдельных видов продукции в товарообороте отчетного периода
 ; в результате ср. изменения цен
Условный индекс и среднеарифметический индекс цен Ласпейреса ; в результате ср. изменения цен
Условный индекс и среднеарифметический индекс цен Ласпейреса
 ; ;  3. Индекс товарооборота (выручки от продаж)
3. Индекс товарооборота (выручки от продаж)
 ; ;  - это абс. измен. товарооборота за счет совместного действия обоих факторов. - это абс. измен. товарооборота за счет совместного действия обоих факторов.
|
 - Мультипликативная модель - Мультипликативная модель
 - Аддитивная модель - Аддитивная модель
 Это доля участия фактора цены в формировании общего прироста товарооборота
Это доля участия фактора цены в формировании общего прироста товарооборота
 Это доля участия фактора объема продукции в формировании общего прироста товарооборота
Индекс переменного состава:
Это доля участия фактора объема продукции в формировании общего прироста товарооборота
Индекс переменного состава:
 Индекс постоянного состава:
Индекс постоянного состава:
 Индекс структурных сдвигов:
Индекс структурных сдвигов:

 ; ; 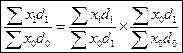 Выборочное наблюдение
Обозначения
Выборочное наблюдение
Обозначения
| Алгоритм решения прямой задачи
Выборочное наблюдение. Обратная задача
Ответ:С вероятностью «такой то» можем утверждать, что для того, чтобы определить среднюю величину изучаемого признака (соответственно долю) для генеральной совокупности по выборочным данным в выборку необходимо взять не менее n элементов.
Корреляция. Регрессия. Коэффициент корреляции (r)
|

Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
 fi – частота появления i- го значения варианта в
fi – частота появления i- го значения варианта в















 ;
xi – элемент выборки
;
xi – элемент выборки



 - для повт. наблюд.
- для повт. наблюд.  - для б/повт
- для б/повт
 - для повт. наблюд
- для повт. наблюд
 - для б/повт
- для б/повт

 , при этом предельная ошибка доли равна
, при этом предельная ошибка доли равна 
 , при этом предельная ошибка выборки равна
, при этом предельная ошибка выборки равна 




 ;
;  ;
; 