|
|
Тема 7. Геометрические характеристики сечения.План: 1. Статические моменты и центр тяжести. 2. Моменты инерции. 3. Изменение моментов инерции при параллельном переносе и повороте осей. 4. Главные оси и главные моменты инерции. 5. Главные моменты инерции простейших сечений 1) Статические моменты и центр тяжести Статическими моментами называют следующие интегралы (рисунок 1):
Рисунок 1
Пусть известны статические моменты относительно осей Найдем статические моменты относительно осей
2) Моменты инерции Моменты инерции сечения определяются так (рисунок 1):
3) Если исходные оси
4) Оси, относительно которых центробежный момент равен нулю, называются главными осями. Главные оси всегда проходят через центр тяжести, (являются центральными). Моменты инерции относительно главных осей называются главными моментами. Относительно главных осей осевые моменты экстремальны ( Литература[1], [2], [4]. Тема 8. Сдвиг. План: 1. Основные понятия. 2. Напряженное состояние и деформации при чистом сдвиге.
1)Сдвигомназывают деформацию, представляющую собой искажение первоначально прямого угла малого элемента бруса под действием касательных напряжений 2) Деформация сдвига оценивается взаимным смещением В предположении равномерного распределения касательных напряжений по сечению площадью А, они определяются по формуле
где Q – поперечная сила в данном сечении. Литература[1], [2], [4]. Тема 9. Изгиб. План: 1. Основные понятия. 2. Эпюры поперечных сил и изгибающих моментов. 3. Чистый изгиб, нормальные напряжения. Касательные напряжения, формула Д.И.Журавского. 4. Расчет на прочность. 1) Изгибомназывается вид нагружения бруса, при котором к нему прикладывается момент, лежащий в плоскости проходящей через продольную ось. При изгибе возникают деформация, при которой происходит искривление оси прямого бруса или изменение кривизны кривого бруса. Брус, работающий при изгибе, называется балкой. Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения. При плоском поперечном изгибе в балке возникают два вида внутренних усилий: поперечная сила Q и изгибающий момент M. Если изгибающий момент 2) В соответствии с методом сечений поперечную силу можно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось у). Изгибающий момент равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси х). 3) При чистом изгибе в поперечных сечениях бруса возникают только изгибающие моменты, а поперечные силы равны нулю. Под действием изгибающих моментов ось бруса искривляется. Исходя из этого, ось бруса принимает форму дуги окружности с радиусом кривизны ρ. В результате изгиба эти сечения наклонятся, образуя между собой угол
при
. Для прямоугольника Для прокатных профилей (двутавра, швеллера, уголка) В случае поперечного изгиба в сечениях балки возникают не только изгибающий момент, но и поперечная сила. Следовательно, в этом случае в поперечных сечениях бруса возникают не только нормальные, но и касательные напряжения, которые вычисляются по формуле Д.И. Журавского.
Условие прочности по касательным напряжениям:
где 4) Условие прочности при изгибе балки в форме призматического стержня получает вид
где Из этого условия формулируют три рода задач на прочность при изгибе. Литература[1], [2], [4]. Тема 10. Устойчивость. План: 1. Основные понятия. 2. Устойчивость продольной формы сжатых стержней в упругой стадии. Формула Эйлера, границы ее применимости.
1) Под устойчивостьюпонимают способность систем сохранять их состояние равновесия или движения во времени под действием малых возмущений. Под неустойчивостью понимают способность систем при действии весьма малых возмущений получать большие перемещения. 2) Формула Эйлера для критической силы при расчете сжатого стержня на устойчивость записывается в виде:
где Пределы применимости формулы Эйлера получены в предположении упругого поведения материала, т.е. при условии:
где При
разделяющей области упругой
получаем:
Для алюминиевого сплава Д16Т (дюраль)
Литература[1], [2], [4]. Содержание практических занятий
Тема 1Входной контроль. План: 1.Составление алгоритма решения задачи. 2. Решение практических задач по теме занятия. Задания: Решение задач по карточкам, выдаваемым преподавателем по векторной алгебре. Литература[3], [8], [11]. Тема 2Составление уравнения равновесия на плоскости. План: 1.Составление алгоритма решения задачи. 2. Решение практических задач по теме занятия. Задания: Решение задач 4.7, 4.18, 4,25-4.28 (Мещерский И.В. Сборник задач по теоретической механике). Решение задач по карточкам, выдаваемым преподавателем. Литература[3], [8], [11]. Тема 3Составление уравнения равновесия в пространстве. План: 1.Составление алгоритма решения задачи. 2. Решение практических задач по теме занятия. Задания: Решение задач 8.7, 8.14, 8.18, 8.25-8.28 (Мещерский И.В. Сборник задач по теоретической механике). Решение задач по карточкам, выдаваемым преподавателем. Литература[3], [8], [11]. Тема 4Расчет ферм. План: 1.Составление алгоритма решения задачи. 2. Решение практических задач по теме занятия. Задания: Решение задач 4.67, 4.68, 4,71, 4.73. (Мещерский И.В. Сборник задач по теоретической механике). Решение задач по карточкам, выдаваемым преподавателем. Литература[3], [8], [11]. Тема 5, 6.Растяжение и сжатие в статически определимых системах. План: 1.Составление алгоритма решения задачи. 2. Решение практических задач по теме занятия. Задания:
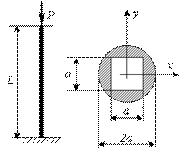
Построить эпюры продольных сил и нормальных напряжений, а также полное его удлинение. Материал стержня — сталь, сечение круглое. Решение задач по карточкам, выдаваемым преподавателем. Литература[3], [4], [9]. Тема 7.Геометрические характеристики сечения. План: 1.Составление алгоритма решения задачи. 2. Решение практических задач по теме занятия. Задания: Пример 1. Определить координаты центра тяжести и осевые моменты инерции сечения в виде круга радиусом r =3а с круговым отверстием радиуса r0 = a, касающимся центра круга (см. рис.).
Пример 2. Определить момент инерции сечения, показанного на рис. 4.12, относительно оси симметрии, a=10 см.
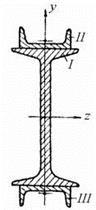
Пример 3. Определить момент инерции симметричного сечения, показанного на рис. 4.13, относительно вертикальной оси симметрии y. Двутавр №10 (ГОСТ 8239-56). Швеллер №5 (ГОСТ 8240-56).
Примечание: Для двутавра №10 (ГОСТ 8239-56): H=10 см, B=7 см, F=14,2 см2, Ix=244 см4, Iy=35,3 см4. Для швеллера №5 (ГОСТ 8240-56): h=5 см, b=3,7 см, F=6,90 см2, Ix=26,1 см4, Iy=8,41 см4, x0=1,35 см. Методические рекомендации по выполнению задания:выбор варианта в приведенной выше таблице производить по последней цифре зачетной книжки. Решение задачи выполнить с использованием формул механики грунтов [2], [5]. Результат работы оформить в виде краткого описания решения задачи. Литература[3], [4], [9]. Тема 8,9 СдвигИзгиб. План: 1.Составление алгоритма решения задачи. 2. Решение практических задач по теме занятия. Задания: Задача № 1 Построить в общем виде эпюры QY и MX для заданной балки.
Таблица1 – Исходные данные к задаче
Методические рекомендации по выполнению задания:выбор варианта в приведенной выше таблице производить по последней цифре зачетной книжки. Решение задачи выполнить с использованием формул [3], [4], [9]. Результат работы оформить в виде краткого описания решения задачи. Задача № 2 Определить размеры поперечного сечения b и h = 2b, если
Таблица1 – Исходные данные к задаче
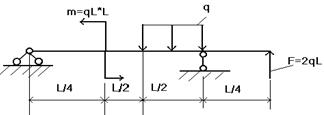
Задача № 3 Построить эпюры поперечных сил и изгибающих моментов, если L2=3 L1.
Таблица1 – Исходные данные к задаче
Методические рекомендации по выполнению задания:выбор варианта в приведенной выше таблице производить по последней цифре зачетной книжки. Решение задачи выполнить с использованием формул [3], [4], [9]. Результат работы оформить в виде краткого описания решения задачи. Литература[3], [4], [9]. Тема 10.Устойчивость. План: 1.Составление алгоритма решения задачи. 2. Решение практических задач по теме занятия. Задания: Стальной стержень длиной L сжимается силой Р. Условия закрепления стержня и форма его перечного сечения показаны на рисунке. Требуется найти размеры поперечного сечения стержня, величину критической силы и коэффициент запаса устойчивости при допускаемом напряжении на сжатие
Таблица1 – Исходные данные к задаче
Методические рекомендации по выполнению задания:выбор варианта в приведенной выше таблице производить по последней цифре зачетной книжки. Решение задачи выполнить с использованием формул [3], [4], [9]. Результат работы оформить в виде краткого описания решения задачи. Литература[3], [4], [9]. 8. Задания для самостоятельной работы 8.1 Дополнительные темы для самостоятельного изучения. Тема 1. Аксиомы статики. Цель –Получить представление об аксиомах статики. Содержание задания. Изучить и кратко описать аксиомы статики Форма отчетности – конспект по теме. Литература[1], [2], [7]. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

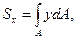
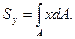
 , параллельных осям
, параллельных осям 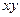 , но смещенных на расстояния
, но смещенных на расстояния  и
и 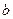 .
.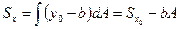 и
и 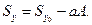


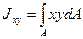 .
. называются осевыми моментами инерции,
называются осевыми моментами инерции, центробежным моментом.
центробежным моментом.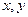 центральные, то при параллельном переносе осей (рисунок 1) моменты инерции изменяются на величину, равную произведению площади на квадрат расстояния между осями
центральные, то при параллельном переносе осей (рисунок 1) моменты инерции изменяются на величину, равную произведению площади на квадрат расстояния между осями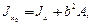
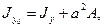
 ), а центробежный момент равен нулю (
), а центробежный момент равен нулю ( 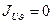 ).
).
 граней 1 – 1 и 2 – 2 малого элемента, называемым абсолютным сдвигом и более полно – относительным сдвигом (углом сдвига)
граней 1 – 1 и 2 – 2 малого элемента, называемым абсолютным сдвигом и более полно – относительным сдвигом (углом сдвига) 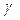 , являющимся безразмерной величиной.
, являющимся безразмерной величиной. 

 ,
, является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы
является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы  изгиб называется поперечным.
изгиб называется поперечным.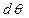 , в связи с чем верхние волокна удлиняются, а нижние - укоротятся. Очевидно, что при этом существует слой, длина которого не изменилась. Назовем его нейтральным слоем и обозначим отрезком СD. Переход от деформаций к нормальным напряжениям
, в связи с чем верхние волокна удлиняются, а нижние - укоротятся. Очевидно, что при этом существует слой, длина которого не изменилась. Назовем его нейтральным слоем и обозначим отрезком СD. Переход от деформаций к нормальным напряжениям 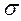 можно осуществить посредством закона Гука:
можно осуществить посредством закона Гука:
 ):
):  , где
, где 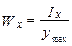 - момент сопротивления сечения при изгибе.
- момент сопротивления сечения при изгибе.
 Для круга
Для круга 
 приводится в таблицах сортамента.
приводится в таблицах сортамента.
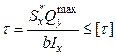
 -максимальное значение поперечной силы в сечении;
-максимальное значение поперечной силы в сечении;  - допускаемое касательное напряжение, оно, как правило, равно половине
- допускаемое касательное напряжение, оно, как правило, равно половине 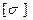 .
.
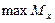 — максимальное значение изгибающего момента (легко определяемое по его эпюре),
— максимальное значение изгибающего момента (легко определяемое по его эпюре),  - допускаемое напряжение на простое растяжение (сжатие).
- допускаемое напряжение на простое растяжение (сжатие).
 - приведённая длина Ясинского,
- приведённая длина Ясинского,  - коэффициент приведения длины стержня к длине шарнирно опёртого по концам стержня.
- коэффициент приведения длины стержня к длине шарнирно опёртого по концам стержня.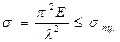
 - предел пропорциональности.
- предел пропорциональности.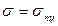 получаем предельное значение гибкости:
получаем предельное значение гибкости:
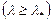 и неупругой
и неупругой 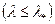 потерь устойчивости стержня. Для малоуглеродистой стали
потерь устойчивости стержня. Для малоуглеродистой стали ,
,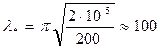 .
. , находим:
, находим: 



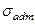 = 120 МПа;
= 120 МПа; 

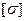 = 160 МПа.
= 160 МПа.