Арифметические вычисления

ВВЕДЕНИЕ

Система компьютерной математики MATLAB (Matrix Lавoratory) переводится с английского как «Матричная лаборатория». Она является одним из эффективнейших средств выполнения научных и инженерных расчетов, их визуализации, обработки результатов эксперимента, анализа и моделирования. Для формулировки и решения задач в среде MATLAB используются понятные математические выражения, близкие к традиционным формулам, связывающие векторные или матричные объекты. Система включает ядро, использующее базовые вычислительные (встроенные) функции, и набор общематематических, графических и проблемно - ориентированных пакетов (Toolboxes), позволяющих изучать и применять современную вычислительную технологию в таких областях, как обработка сигналов и изображений, моделирование, системы управления, системы связи, нейронные сети и многие другие.

Данное учебное пособие предназначено для освоения основных навыков по самостоятельному выполнению расчетов на компьютере в командном (диалоговом) режиме, возможно, после консультации с преподавателем. В нем предоставлены примеры реального применения системы MATLAB, имеющие в основном математическую направленность, к которым в дальнейшем можно обращаться при решении собственных задач с различной проблемной ориентацией. Это задачи высшей и вычислительной математики, теории электрических цепей, теории электро - связи и других дисциплин, изучаемых в технических ВУЗах. Материал представлен сжато. Предполагается, что он усваивается в непосредственном контакте с системой, когда численные и графические результаты расчетов, представленные в примерах, будут получены пользователем прямо на экране.

Предполагается также, что пользователь знаком с каким-либо языком программирования, например Pascalили Basic, с приемами, общими для Windows - приложений и математическими постановками рассматриваемых задач.

Для реализации всех рассматриваемых примеров на используемом компьютере должны быть установлены следующие компоненты системы: ядро MATLAB, пакет Symbolic Math Toolbox.

ГЛАВА 1 ЗНАКОМСТВО С MATLAB И ПРОСТЕЙШИЕ ВЫЧИСЛЕНИЯ

Данная глава посвящена описанию рабочей среды MATLAB6.x и выполнению элементарных операций с числами и массивами в командном режиме (режиме калькулятора). В этой главе рассматриваются особенности задания в MATLAB действительных и комплексных чисел, форматы их представления, правила использования переменных, а также способы задания векторов и матриц. Здесь также рассмотрены встроенные математические функции и способы сохранения переменных для их использования в последующих сеансах работы в MATLAB. Обсуждаются некоторые распространенные затруднения, с которыми можно столкнуться. Рекомендуется читать эту главу и параллельно работать с командами, экспериментировать с вариантами примеров.

Рабочая среда MATLAB

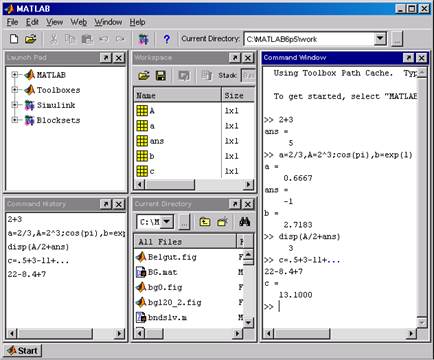
При работе в Windows запустить систему MATLAB можно из меню Пуск (стартового меню) этой операционной системы. Альтернативным вариантом запуска MATLAB является двойной щелчок на ярлыке системы MATLAB, расположенном на рабочем столе Windows.

Запуск MATLAB6.x отображает на экране окно рабочей cреды, подобное показанному на рис.1.1.

Рис 1.1

Окно рабочей среды (графический интерфейс) состоит из следующих основных элементов:

строка меню;

панель инструментов с кнопками и раскрывающимся списком;

окно с Launch Pad (Панель запуска) содержит дерево файловой системы, где отображены только установленные на компьютере разделы расширений системы MATLAB. С помощью этого окна можно запустить любой из них;

окно Workspase (Рабочее пространство), из которого можно получить простой доступ к переменным, используемым в данном сеансе работы;

окно Command History (История команд), предназначенное для просмотра и повторного вызова ранее введенных команд;

окно Current Directory (Текущий каталог), в котором отображается список файлов и вложенных папок активного в данный момент каталога;

окно Command Window(Окно команд) предназначено для ввода чисел, переменных, выражений и команд, для промотра результатов вычислений, для отображения текстов выполняемых программ, а также для вывода сообщений об ошибках;

строка состояния, где отображаются сообщения системы.

Пользователь может настроить окно рабочей среды по своему усмотрению. Можно, например, изменить местоположение и размер внутренних окон приемами, общими для Windows - приложений. Отобразить или скрыть соответствующие окна можно с помощью команд меню View(Вид) основного меню MATLAB. Например, для отображения полной рабочей среды (рис. 1.1) надо выбрать команду View => Desktop Layout => Five Panel. Любое из внутренних окон полной рабочей среды можно закрыть щелчком по кнопке с крестиком в правом верхнем углу.

Арифметические вычисления

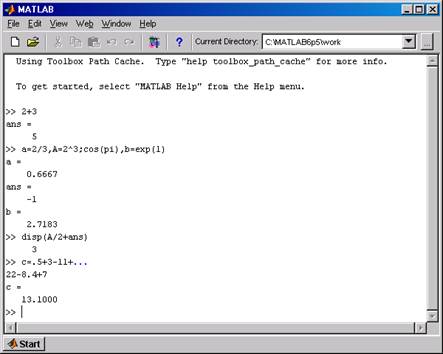
Работа в среде MATLAB может осуществляться либо в программном режиме (см. Главу 4), либо в командном режиме (режиме калькулятора, диалоговом режиме) по правилу «задал вопрос, получил ответ». Это превращает MATLAB в необычайно мощный калькулятор, который способен производить не только обычные для калькулятора вычисления, но и операции с векторами и матрицами, комплексными числами, рядами и полиномами. Можно почти мгновенно задать и вывести графики различных функций: от простой синусоиды до сложной трехмерной фигуры.

Основным элементом командного режима работы с системой является главное или командное окно Command Window . Оно активизируется командой View => Desktop Layout => Command Window Only основного меню MATLAB. Структура командного окна аналогична структуре Windows - приложений (рис. 1.2).

Рис. 1.2

Строка в текстовом поле командного окна, отмеченная символом приглашения >>с мигающим курсором, называется строкой ввода или командной строкой. Она предназначена для ввода с клавиатуры команд, чисел, имен переменных и знаков операций, составляющих выражение. Для того, чтобы система MATLAB выполнила введенную команду или вычислила заданное выражение, следует нажать клавишу <Enter>(Ввод).

При вводе курсор может находиться в любом месте командной строки. Введенные выражения вычисляются, а результаты вычислений и выполнения команд появляются в одной или нескольких строках командного окна – строках вывода.

В результате многократных вычислений (нажатий клавиши <Enter>) в командном окне автоматически производится вертикальная протяжка (scrolling): строки сдвигаются на одну позицию вверх, а внизу появляется строка ввода с символом приглашения >>. Информация, которая покинула видимую часть окна, не исчезает. В MATLAB ранее введенные строки команд представляют собой «историю» и запоминаются в стеке команд (см. разд. 1.8).

Для просмотра выполненных команд и результатов вычислений, не умещающихся на экране, имеются полосы горизонтальной и вертикальной протяжки. Использование полос протяжки ничем не отличается от других Windows - приложений. Можно также осуществлять протяжку командного окна с помощью клавиш <PageUp>, <PageDown>, <Ctrl+Home>и<Ctrl+End>.

Клавиши <↑> и <↓>, которые в текстовых редакторах служат для перемещения вверх или вниз по экрану, в MATLAB работают иначе. Они используются для возврата в строку ввода ранее выполненных команд с целью их повторного выполнения или редактирования. После первого нажатия клавиши <↑> в строке ввода отобразится последняя введенная команда, при втором нажатии – предпоследняя и т. д. Клавиша <↓> осуществляет прокрутку команд в противоположном направлении.

Иными словами, текстовое поле окна Command Window располагается в двух принципиально разных зонах: зоне просмотра и зоне редактирования. Зона редактирования находится в командной строке, а вся остальная информация видимой части командного окна – в зоне просмотра.

Пока не нажата клавиша <Enter>, вводимое выражение может быть отредактировано или удалено. В зоне просмотра уже ничего нельзя исправить. Если поместить в нее курсор и нажать какую - либо клавишу на клавиатуре, курсор будет автоматически перемещен в строку ввода, расположенную в зоне редактирования. В то же время, с помощью клавиш <←> и <→> можно перемещать курсор в командной строке.

Невозможность редактирования ранее введенной команды простой установкой курсора в нужную строку является одной из особенностей системы MATLAB.

Сеанс работы с системой MATLABназывается сессией. Иными словами, сессия – это все то, что отображается в командном окне в процессе работы с системой. Команды сессии автоматически образуют список, который выводится в окне Command History, а значения переменных сохраняются в окне Workspase (рис. 1.1).

Например, сессия на рис. 1.2 отображает результаты последовательного ввода четырех команд. Обсудим эти результаты и отметим некоторые особенности вычислений в системеMATLAB:

>> 2+3

ans =

Результату выполненной операции не было присвоено имя, поэтому при выводе он был автоматически обозначен символом ans (ansver – ответ). Под этим именем результат вычислений хранится в памяти компьютера и его можно использовать в последующих вычислениях до тех пор, пока в ходе работы не будет получен новый непоименованный результат. Результат вычислений выводится в строках вывода, не содержащих знака приглашения >>;

>> a=2/3,A=2^3;cos(pi),b=exp(1)

a =

0.6667

ans =

-1

b =

2.7183

В одной командной строке можно ввести несколько команд, разделяя их запятыми либо точками с запятой. Система MATLAB выполняет каждую команду, за которой следует запятая, и отображает результаты в отдельных строках. Результат выполнения команды, за которой следует символ <;>, на экран не выводится, но он сохраняется в памяти и может быть использован в последующих вычислениях.

Знаком присваивания является знак =, а не комбинированный знак :=, принятый, например, в языке программирования Pascalили в системе символьной математики Maple.

После ввода этой командной строки вычисляются и сохраняются в памяти значения выражений a=2/3=0,б667, A=2³=8, ans=cosp =-1, b=e¹=e=2,7183 (e – основание натурального логарифма). Значение переменной A, в отличие от a, ans, b, не выводится на экран из-за символа <;>. При вычислении cosp использовалась системная переменная pi – число p. Число e системной переменной не является, и для его вычисления использована встроенная элементарная функция exp(1). Функции записываются строчными буквами, а их аргументы указываются в круглых скобках. Аргумент встроенной тригонометрической функции cos задан в радианах;

>> disp(A/2+ans)

Команда disp (от слова «дисплей») вычисляет выражение 2³/2+cosp и выводит ответ, но не присваивает его переменной ans, как при обычных вычислениях:

>> A/2+ans

ans =

В дальнейшем disp используется для предотвращения вывода лишней строки ans = в наглядных документах;

>> c=.5+3-11+...

22-8.4+7

c =

13.1000

Иногда требуется ввести в окне Command Window команду, которая слишком длинна, чтобы уместиться на одной строке. При приближении к концу строки можно ввести … (три последовательные точки), нажать клавишу <Enter>и продолжить набор команды на следующей строке. При этом вы не увидите на новой строке символа приглашения >>.

Сессия на рис.1.2 содержит только правильные команды и результаты их выполнения. В общем случае сессия является результатом проб и ошибок. Ее текст, наряду с правильными определениями, содержит сообщения и предупреждения об ошибках (см. разд. 1.8), переопределения функций и переменных, использованную справочную информацию команды help (см. приложение.1, рис. П1, рис. П.2). Если сессия сильно «засорена» лишней информацией, диалог пользователя с системой затрудняется.

Команда очистки экрана clc

>> clc

стирает содержание командного окна MATLAB и размещает символ приглашения >> в левом верхнем углу пустого экрана.

Эта команда, однако, оставляет неизменным содержимое окон Command History и Workspase. Поэтому в «чистом» командном окне можно пользоваться значениями переменных, полученных до ввода команды clc.

Если же появится необходимость отредактировать или повторить ранее выполненную команду, то это легко осуществить с помощью окна Command History. Подробнее работа с оконами Command History и Workspase обсуждается в разделах 1.8 и 1.9.

Переменные– это именованные объекты, хранящие какие – либо данные.

Переменные могут быть числовыми, матричными или символьными, что зависит от типа хранящихся в них данных. Типы переменных заранее не декларируются. Они определяются выражением, значение которого присваиваивается переменной, т.е. пользователь не должен заботиться о том, какие значения будет принимать переменная (комплексные, вещественные или целые).

Имя переменной (ее идентификатор) может содержать до 31 символа и не должно совпадать с именами других переменных, функций, команд и системных переменных MATLAB. Имя переменной должно начинаться с буквы, может содержать цифры и символ подчеркивания. Среда MATLAB чувствителена к регистру букв (переменные a и A не идентичны).

В MATLAB существует несколько имен переменных, являющихся зарезервированными. Переменные с такими именами называются системными. Они задаются после загрузки системы и могут использоваться в арифметических выражениях. Системные переменные могут быть переопределены, т. е. при небходимости им можно присвоить другие значения.

Ниже перечислены основные системные переменные MATLAB:

ans – результат вычисления последнего не сохраненного пользователем выражения;

i, j – мнимая единица (), используемая для задания мнимой части комплексных чисел;

Inf (infinity) – обозначение машинной бесконечности;

NaN – сокращение от слов Not-a-Number (не число), принятое для обозначения неопределенного результата (например, 0/0 или Inf/Inf).

pi – число π ( p=3,141592653589793);

eps – погрешность операций над числами с плавающей точкой, т.е интервал между числом 1.0 и следующим ближайшим числом с плавающей точкой равен 2.2204e-16 или 2^-52;

realmin – минимальное по модулю вещественное число (2.2251e-308 или 2^-1022);

realmax – наибольшее по модулю вещественное число (1.7977e+308 или 2¹⁰²³).

Приоритеты арифметических операций системы MATLAB в порядке убывания следующие:

1. Возведение в степень <^>.

2. Умножение <*> и деление (слева направо </>, справа налево <\>).

3. Сложение <+> и вычитание <–>.

Выполнение операций одинакового приоритета происходит в порядке слева направо. Для изменения порядка выполнения арифметических операторов следует использовать круглые скобки. Кроме арифметических операторов, в MATLAB имеются операторы отношения и логические операторы (см. разд. 4.1).

Полный список операторов и справочную информацию по любому из них можно получить в разделе ops справочной системы MATLAB, используя команды helpили doc (см. Приложение 1).

Основу большинства расчетов составляют вычисления значений арифметических выражений. В них в качестве операндов могут выступать константы, переменные или функции. В отличие от большинства алгоритмических языков, в MATLAB допускается использование операндов - массивов (см. разд. 1.6, 1.7, 1.10). В этом случае результатом вычисления выражения также может быть массив.

Выражения, помещенные между двумя апострофами (заключенные в символьные скобки ' '), рассматриваются как строчные и не вычисляются, даже если в них содержатся математические выражения. Чаще всего они применяются для задания параметров функций и их нечисловых значений, вставки текста в графические объекты, а также для описания символьных переменных и выражений. Так, ввод строки '2+3' приводит к результату

>> '2+3'

ans =

2+3

а не 5.

При выводе графиков символы, помещенные между апострофами, определяют цвет линий графика, их тип и тип маркера, которым метятся линии (Глава 5).

Вещественные числа

Число – простейший объект системы MATLAB, представляющий количественные данные. Основным типом данных, с которым производятся вычисления в системе MATLAB, являются десятичные числа. Они приближают с заданной точностью произвольные вещественные (действительные) числа. Десятичные числа, используемые в MATLAB, могут быть целыми и дробными, например: 0, 1, -93, 7.5674, 0.00000047.

Возможно представление чисел в экспоненциальной форме с указанием мантиссы и порядка числа: 3.3333e -4; -75.8e13.

Для отделения порядка числа от мантиссы применяется символ e, т.е. запись 3.3333e -04 соответствует записи 3.3333×10^-4 или 0.00033333.

Ввод чисел возможен в любом удобном для пользователя виде. Например, проще набрать 10e8 или 1.0e9, чем 1 000 000 000, а результат будет тот же самый. Пробел между цифрами и символом e при вводе не допускается, так как это приводит к сообщению об ошибке:

>> 10 e8

??? 10 e8

Error: Missing operator, comma, or semicolon.

В качестве разделителя целой и дробной частей числа используется точка, а не запятая.

При вводе числа с нулевой целой частью ноль может опускаться: .5 равнозначно 0. 5.

Хотя задавать вещественные числа можно в любой из указанных выше форм, на машинном уровне системы MATLAB они представляются в форме с мантиссой и показателем степени. Этот основной тип данных называется double (формат с двойной точностью). Он задается по умолчанию, и даже целые числа представляются системой MATLAB на машинном уровне в той же форме, что и дробные числа.

Под мантиссу и показатель степени (на машинном уровне используется двоичная система записи) отводится 8 байт памяти. В результате для десятичных чисел достигается точность порядка 15 значащих цифр. Они принимают по модулю значения от 2.2250738507201e -308 до 1.797693134862316e+308. Для этих чисел зарезервированы имена realmin и realmax.

Все операции над числами MATLAB выполняет по умолчанию в формате double. Такой формат удовлетворяет подавляющему большинству требований к численным расчетам, но совершенно не подходит для символьных вычислений с произвольной (абсолютной) точностью (Глава 7).

В MATLABтакже существует тип данных single, который снижает требования к памяти в два раза (под мантиссу и показатель степени отводится 4 байта). Но при сложных вычислениях в этом случае возрастает вероятность получить результат с большой погрешностью.

Существуют и целые типы данных: int8, uint8, int16, uint16, int32, uint32, int64, uint64. Под них отводится 8, 16, 32 и 64 байта соответственно.Буква u соответствует беззнаковым типам данных с диапазоном от 0 до некоторого максимального положительного значения.

Для того чтобы переменная получила тип данных, отличный от double, применяется явный квалификатор , совпадающий с названием типа.

Например,

>> x=int32(3.2)

определяет переменную целого типа int32.

Подробную информацию о перечисленных типах данных можно получить с помощью команд doc double, doc single, doc int8, doc uint8.

Не нашли, что искали? Воспользуйтесь поиском по сайту: