
|
|
Теоремы Розенблатта об элементарных перцептронах12
Первая теорема Розенблатта доказывает существование элементарного перцептрона, способного выполнить любую классификацию заданного множества черно-белых изображений, т.е. она показывает, что перцептрон является универсальным устройством для решения любой задачи классификации изображений. Теорема 2.1. Пусть дано множество Доказательство. Для доказательства достаточно показать существование хотя бы одного элементарного перцептрона, способного выполнить произвольную классификацию C(W). Рассмотрим перцептрон, каждому изображению
где
wjk – вес связи между j-м S-элементом и k-м А-нейроном; Для каждого изображения Wk зададим веса wjk
При предъявлении любого изображения
где В этом случае все изображения подмножества W 1 будут кодироваться положительным единичным выходным сигналом нейронной сети, а подмно-жества W 2 – отрицательным, т.е. будет правильно выполняться классификация C(W) исходного множества W изображений. Хотя построенная таким образом нейронная сеть не имеет существенного практического значения, однако ее наличие показывает, что элементарный перцептрон является универсальным устройством классификации любого множества изображений на два класса. В том случае, когда число изображений множества W превышает число А-нейронов, элементарный перцептрон теряет свою универсальную способность классифицировать изображения. Теорема 2.2. Если число n изображений в множестве W больше числа А-элементов элементарного перцептрона, то существует некоторая класси-фикация С(W) множества W черно-белых изображений на два подмножества W 1, W 2, которая не может быть выполнена перцептроном. Теорема 2.3. Для любого элементарного перцептрона с конечным числом А-нейронов вероятность выполнения классификации С(W), которая выбирается из равномерного распределения по всем возможным классификациям множества Теорема 2.1 доказывает существование элементарного перцептрона, способного выполнять любую заданную классификацию С(W) изображений некоторого множества W на два класса, однако она не указывает алгоритмов достижения этой способности в процессе обучения нейронной сети. Розенблаттом была доказана важная для теории элементарных перцептронов теорема о наличии таких алгоритмов для α-перцептронов. Рассмотрим некоторую классификацию С(W) множества W изображений на два подмножества W 1, W 2, которая может осуществляться перцептроном с R-элементом, выходной сигнал которого удовлетворяет условиям:
Положим также, что:
Определение 2.9. Метод коррекции ошибок без квантования – этот метод системы подкрепления с коррекцией ошибок, когда при ошибочной реакции R-элемента с порогом q на некоторое изображение Теорема 2.4. Пусть дан элементарный α-перцептрон, множество черно-белых изображений Теорема 2.4 доказывает наличие сходящегося детерминированного метода обучения с коррекцией ошибок для элементарного перцептрона с квантованием или без квантования подкрепления. Следующая теорема доказывает, что обучение элементарного перцептрона может быть выполнено и при менее жестких требованиях к виду коррекции – методом коррекции ошибок со случайным законом подкрепления, когда при появлении ошибки сигнал подкрепления формируется как в α-системе, но знак подкрепления с вероятностью 0,5 может быть положительным или отрицательным. Теорема 2.5. Пусть дан элементарный α-перцептрон с конечным числом значений весов связей между R- и А-нейронами, множество черно-белых изображений Естественно, что метод со случайным знаком подкрепления требует большего объема вычислений при обучении перцептрона, чем прямая коррекция ошибок с квантованием или без квантования подкрепления. Еще большего объема вычислений требует метод, в котором производится случайный выбор не только знака, но и величины подкрепления. Розенблаттом доказана теорема о том, что с вероятностью, равной единице, обучение перцептрона может быть выполнено за конечное время и методом коррекции случайными возмущениями, когда подкрепление формируется как в α-системе, но при этом величина η и знак подкрепления для каждого веса связи выбираются отдельно и независимо в соответствии с некоторым заданным законом распределения вероятностей. Менее универсальной системой подкрепления, чем α-система и системы со случайным формированием подкрепления, является γ-система. Это доказыва-ет следующая теорема Розенблатта. Теорема 2.6. Пусть дан элементарный γ-перцептрон, подмножество Доказательство. Пусть функционирование А-нейронов определяется выражением:
где Пусть также каждый А-нейрон возбуждается только одним изображением из множества W, а классификация C(W) осуществляется с помощью R-элемента, функционирование которого описывается соотношением:
где
ЗАДАЧА
Формировать два образа и выполнить обучение элементарного перцептрона с бинарными S- и A-нейронами и биполярным R-нейроном (рис. 2.3) их распознавание.
При этом потребуем, чтобы при предъявлении первого образа на выходе R-элемента был сигнал “–1”, при появлении второго – сигнал “+1”.
Задать в таблицах 2.1 и 2.2 веса связей
Таблица 2.1. Веса
Таблица 2.2. Веса
Подать на вход перцептрона 1 образ.. Единичные сигналы с выходов возбужденных бинарных S-нейронов через связи, весовые коэффициенты которых заданы табл. 2.1, поступают на входы А-нейронов. Суммарный входной сигнал на входе i-го А-элемента определяется соотно-шением:
где
Аналогично вычислить сигналы на входах остальных А-элементов. Результаты этих вычислений свести в табл. 2.3.
Таблица 2.3. Величины сигналов на входах A-элементов
Для упрощения расчетов пороги
Для обеспечения работоспособности нейронной сети порог
Выходной сигнал А-элементов рассчитать по соотношению
Использовать для настройки перцептрона α-систему подкрепления при величине сигнала подкрепления η равном 0,1 и при предъявлении последовательности образов в моменты времени t1, t2, t3, … . Процесс адаптации весов связей между R- и A-нейронами занести в табл. 2.4.
Таблица 2.4. Адаптация весов связей перцептрона с помощью подкрепления
Выходное значение R-элемента рассчитать по соотношению:
где 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 черно-белых изобра-жений на некоторой сетчатке
черно-белых изобра-жений на некоторой сетчатке  , тогда для любой классификации C(W) множества W черно-белых изображений на два подмножества W 1, W 2 существует не пустой класс элементарных перцептронов с сетчаткой S, способных выполнить эту классификацию.
, тогда для любой классификации C(W) множества W черно-белых изображений на два подмножества W 1, W 2 существует не пустой класс элементарных перцептронов с сетчаткой S, способных выполнить эту классификацию. на сетчатке S которого соответствует один А-элемент – нейрон Ak, функционирование которого определяется выражением:
на сетчатке S которого соответствует один А-элемент – нейрон Ak, функционирование которого определяется выражением: (2.24)
(2.24) – выходной сигнал нейрона Аk;
– выходной сигнал нейрона Аk;  – сигнал на входе нейрона Аk,
– сигнал на входе нейрона Аk, ; (2.25)
; (2.25) - выходной сигнал j-го S-элемента,
- выходной сигнал j-го S-элемента, (2.26)
(2.26) – порог срабаты-вания k-го А-элемента;
– порог срабаты-вания k-го А-элемента; 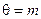 .
. соотноше-нием:
соотноше-нием: (2.27)
(2.27) выражением вида:
выражением вида:
 – входной сигнал R-элемента.
– входной сигнал R-элемента. изображений на два класса, стремится к нулю при n, стремящемся к бесконечности.
изображений на два класса, стремится к нулю при n, стремящемся к бесконечности. (2.28)
(2.28) (2.29)
(2.29) к весу каждой из связей, соединяющих активные А-нейроны с R-элементом, прибавляется величина
к весу каждой из связей, соединяющих активные А-нейроны с R-элементом, прибавляется величина  , где коэффициент
, где коэффициент  выбирается из условия, что после коррекции весов связей выполняется соотношение (2.28), т.е. перцептрон правильно классифицирует предъявленное изображение. В методе коррекции ошибок с квантованием применяется это же правило коррекции весов связей, но величина
выбирается из условия, что после коррекции весов связей выполняется соотношение (2.28), т.е. перцептрон правильно классифицирует предъявленное изображение. В методе коррекции ошибок с квантованием применяется это же правило коррекции весов связей, но величина  подаются на вход перцептрона в произвольной последовательности, в которой каждое из них появляется неоднократно, через конечное число предъявлений других изображений. Тогда процесс обучения перцептрона методом коррекции ошибок ( с квантованием или без квантования подкрепления) независимо от начальных значений весов связей между R- и А-элементами всегда приводит за конечное число итераций к множеству весов связей, с помощью которых α-перцептрон может выполнить заданную классификацию изображений.
подаются на вход перцептрона в произвольной последовательности, в которой каждое из них появляется неоднократно, через конечное число предъявлений других изображений. Тогда процесс обучения перцептрона методом коррекции ошибок ( с квантованием или без квантования подкрепления) независимо от начальных значений весов связей между R- и А-элементами всегда приводит за конечное число итераций к множеству весов связей, с помощью которых α-перцептрон может выполнить заданную классификацию изображений.
 – соответственно выходной и входной сигналы k-го A-нейрона;
– соответственно выходной и входной сигналы k-го A-нейрона; 
 – соответственно выходной и входной сигналы R-нейрона. Выберем классификацию C(W), которая относит все изображения к классу
– соответственно выходной и входной сигналы R-нейрона. Выберем классификацию C(W), которая относит все изображения к классу  или к классу
или к классу  . Очевидно, что в первом случае решение существует только тогда, когда веса всех связей между R- и А-элементами положительны (или отрицательны, если все изображения относятся к классу
. Очевидно, что в первом случае решение существует только тогда, когда веса всех связей между R- и А-элементами положительны (или отрицательны, если все изображения относятся к классу  ). Если для первого случая начальные веса всех связей между R- и А-нейронами отрицательны, а для второго – положительны, то в силу свойства консервативности γ-системы подкрепления относительно суммы всех весов связей между R- и А-нейронами, она не сможет выполнить правильную настройку весов связей перцептрона для рассматриваемой классификации C(W).
). Если для первого случая начальные веса всех связей между R- и А-нейронами отрицательны, а для второго – положительны, то в силу свойства консервативности γ-системы подкрепления относительно суммы всех весов связей между R- и А-нейронами, она не сможет выполнить правильную настройку весов связей перцептрона для рассматриваемой классификации C(W).
 (
(  ),
),  (
(  ) соответственно между бинарными S- и A-нейронами и между A-нейронами и биполярным нейроном R с помощью генератора случайных чисел, генерирующего их из конечного множества {0,1; 0,2; …; 0,9}.
) соответственно между бинарными S- и A-нейронами и между A-нейронами и биполярным нейроном R с помощью генератора случайных чисел, генерирующего их из конечного множества {0,1; 0,2; …; 0,9}. связей перцептрона между R- и A-элементами
связей перцептрона между R- и A-элементами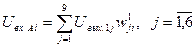 , (2.8)
, (2.8) – сигнал на входе i-го А-нейрона;
– сигнал на входе i-го А-нейрона;  – сигнал на выходе j-го S-ней-рона; wji – вес связи между j-м S-нейроном и i-м А-элементом.
– сигнал на выходе j-го S-ней-рона; wji – вес связи между j-м S-нейроном и i-м А-элементом. всех А-нейронов принять одинаковыми
всех А-нейронов принять одинаковыми
 . (2.9)
. (2.9)
 -системы
-системы



















 – порог R-элемента,
– порог R-элемента,