|
Структурные схемы операторов цикла
Обозначения применяемые в графических алгоритмах
| блок начала – конца алгоритма
| 
| | блок ввода – вывода данных
|

| | арифметический блок
|

| | вызов функций
|  
| | условный блок
| 
| | линейный процесс
| 
| | разветвляющийся процесс
| 
| | циклический процесс
| 
|
Структурные схемы условного оператора
if(выражение){ операторы; }

| if(выражение){операторы;}
else{операторы;}

|
Структурная схема оператора выбора (варианта)
| switch(R)
{
case R1: операторы;
break;
caseR2: операторы;
break;
. . . . .
case RN: операторы;
break;
default: операторы;
}
| где R - выражение,
R1, R2, …. RN,.значения, которые может принять выражение.
|

Структурные схемы операторов цикла
с параметрами
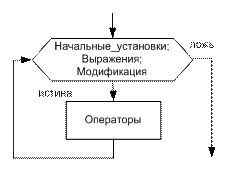
for(начальные_установки; выражение; модификация)
{ операторы; }
 Блок-схема цикла с параметром (for)
Блок-схема цикла с параметром (for)
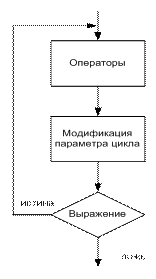
| с предусловием
while(выражение)
{
операторы;
модификация цикла;
}

| с постусловием
do{
операторы;
модификация цикла;
} while( выражение);
|
Алгоритмы для решения задач
|
| Поиск наибольшего общего делителя двух натуральных чисел
(целых положительных чисел), используется алгоритм Евклида:
уменьшается каждый раз большее из чисел на величину меньшего.
Входные данные: А, В – натуральные числа – тип int.
Выходные данные: наибольший общий делитель (нод), тип int.
Проверка
А=25, В=10; нод = 5
Использовать операторы while, if else.
| 
| |
| Вычисление суммы четных натуральных чисел
Входные данные: N – целое число (количество суммируемых чисел) – тип int.
Выходные данные: S сумма целых чисел, тип int.
Вспомогательные переменные: i – параметр цикла, принимает значение 2, 4, 6, 8, ….
Сделать варианты с использованием операторов:
1 while
2 do while
3 for
| 
| |
| Вычисление факториала
Входные данные: N – целое число, чей факториал нужно вычислить ;
Выходные данные: fakt - факториал – произведение чисел от 1 до N
Вспомогательные переменные: i – параметр цикла.
| 
| |
| Поиск максимального числа в последовательности
Входные данные: N – количество чисел – тип unsigned int.;
X– вещественное число, тип float.
Выходные данные:
Мах- максимальное число, тип float.
Вспомогательные переменные: i – параметр цикла.
| 
| |
| Определение количества изменения знака последовательности (разы)
Входные данные: N – количество чисел – тип unsigned int.;
X, У– вещественные числа, тип double.
Выходные данные:
К- количество раз смены знака.
Вспомогательные переменные: i – параметр цикла.
Примечание: признак смены знака – произведение двух соседних чисел меньше 0.
| 
| |
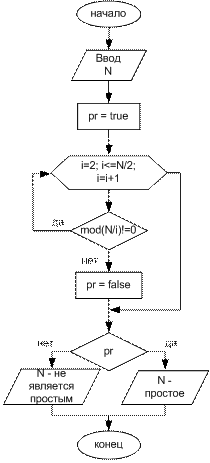
| Определение простого числа
Входные данные: N – целое число;
Выходные данные: сообщения.
Вспомогательные переменные: i – параметр цикла,
pr – признак, тип bool.
Примечания:
1. Число N - простое, если оно делится на 1 или на само себя, т.е. нельзя разложить на множители, отличные от 1 или N.
2. Первоначально устанавливается признак pr=true. Это означает число N – простое. Если в процессе анализа N окажется непростым числом, то признаку присваивается значение false.
3. mod – взятие остатка от деления. Это соответствует операции в языке С++ N % i.
| 
|
| Алгоритм решения квадратного уравнения:
нахождение действительных и комплексных корней уравнения типа ax2 + bx + c = 0.
| Входные данные: a, b, c – коэффициенты квадратного уравнения – тип double.
Выходные данные: х1, х2 – действительные корни квадратного уравнения – тип double., либо х1 (действительная часть комплексного числа) и х2(мнимая часть комплексного числа) – тип double.
Вспомогательные переменные: переменная d, где будет храниться дискриминант квадратного уравнения тип double.
Этапы решения:
1. Ввод коэффициентов a, b, c.
2. Вычисление дискриминанта по формуле d = b2-4ac.
3. Проверка знака дискриминанта.
Если d>=0, то корни действительные  , ,  , вывод на экран ответа.
Если d<=0, то корни комплексные: х1 ± ix2. При этом х1 – действительная часть комплексного числа, равная , вывод на экран ответа.
Если d<=0, то корни комплексные: х1 ± ix2. При этом х1 – действительная часть комплексного числа, равная  , х2 – мнимая часть числа, равная , х2 – мнимая часть числа, равная  . Вывод на экран ответа. . Вывод на экран ответа.
| 
| Написать программу решения квадратного уравнения по заданному алгоритму в консольном приложении.
Текст программы должен быть прокомментирован.
Примерный интерфейс программы:
Решение квадратного уравнения: a*x^2 + b*x + c = 0
Выполнил студент ХХХХ, группа ХХХ
Введите значение коэффициента а -> хх
Введите значение коэффициента b -> хх
Введите значение коэффициента c -> хх
Результаты вычислений - корни действительные/мнимые:
х1 = хх, х2 = хх
Протестировать программу на входных данных:
| вход
| выход
| | a
| b
| c
| x1
| x2
| | -6
|
|
| -0.6385
| 1.3052
| | -6
|
| -5
| 0.3333 + i0.8498
| 0.3333 - i0.8498
|
| Алгоритм решения кубического уравнения:
нахождение действительных и комплексных корней уравнения типа ax3 + bx2 + cx+d = 0.
(см. справочник по математике)
| Входные данные: a, b, c, d – коэффициенты кубического уравнения – тип double.
Выходные данные: х1, х2, х3 – действительные корни кубического уравнения – тип double.,
либо х1 действительный корень, а два остальных –комплексные корни– тип double.
Вспомогательные переменные: переменная D , где будет храниться дискриминант кубического уравнения, а также переменные r, s, t, p, q, , u, v , h, g– тип double.
Этапы решения:
1. Ввод коэффициентов a, b, c, d.
2. Коэффициенты уравнения разделить на коэффициент a (уравнение приводится к каноническому виду), где r=b/a; s=c/a; t=d/a.
3. В каноническом уравнении сделать замену переменной х=у-r/3, получается приведенное уравнение типа y3+py+q=0, где
 и и  .
4. Рассчитать число корней приведенного уравнения (зависит от дискриминанта D). .
4. Рассчитать число корней приведенного уравнения (зависит от дискриминанта D).
 5. Проанализировать дискриминант.
6. При отрицательном дискриминанте будут три действительные корня. Чтобы их рассчитать, надо воспользоваться формулами:
5. Проанализировать дискриминант.
6. При отрицательном дискриминанте будут три действительные корня. Чтобы их рассчитать, надо воспользоваться формулами:
 и и  7. Произвести расчет х1, х2, х3:
7. Произвести расчет х1, х2, х3:

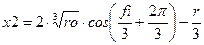
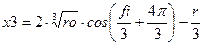 8. Вывести результаты х1, х2, х3.
9. При положительном дискриминанте будут три корня (один – действительный, два – комплексных). Чтобы их рассчитать, надо воспользоваться формулами Кардано (подстановка):
- если выражение
8. Вывести результаты х1, х2, х3.
9. При положительном дискриминанте будут три корня (один – действительный, два – комплексных). Чтобы их рассчитать, надо воспользоваться формулами Кардано (подстановка):
- если выражение  , то , то
 и и  ;
- если выражение ;
- если выражение  , то , то
 и и  При помощи этих выражений получить:
- действительный корень
При помощи этих выражений получить:
- действительный корень  ;
- комплексные корни, где ;
- комплексные корни, где
  и и   .
10 Вывести x1, .
10 Вывести x1, 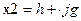 , , 
|  Примечания:
1. использовать математические функции – cos, acos, sqrt, pow, fabs, которые находятся в библиотеке math.h
1 при вычислении
Примечания:
1. использовать математические функции – cos, acos, sqrt, pow, fabs, которые находятся в библиотеке math.h
1 при вычислении  необходимо сделать приведение типов – sqrt((double)3)
2. при вычислении необходимо сделать приведение типов – sqrt((double)3)
2. при вычислении  необходимо сделать приведение типов pow((…..),(double)1/3));
3. j (i) – признак мнимой части комплексного числа, нужен только для формирования вывода в задаче. необходимо сделать приведение типов pow((…..),(double)1/3));
3. j (i) – признак мнимой части комплексного числа, нужен только для формирования вывода в задаче.
| Написать программу решения кубического уравнения по заданному алгоритму в консольном приложении.
Текст программы должен быть прокомментирован.
Примерный интерфейс программы:
Решение кубического уравнения: a*x^3+ b*x^2 + c*x + d = 0
Выполнил студент ХХХХ, группа ХХХ
Введите значение коэффициента а -> хх
Введите значение коэффициента b -> хх
Введите значение коэффициента c -> хх
Введите значение коэффициента d -> хх
Результаты вычислений - корни действительные/мнимые:
х1 = хх, х2 = хх, x3=xx
Протестировать программу на входных данных:
| вход
| выход
| | a
| b
| c
| d
| x1
| x2
| x3
| | -6
|
| -5
|
| 0.7466
| -0.0399 + j0.9441
| -0.0399 - j0.9441
| | 0.1
| 2.0
| 10.0
| 0.5
| -10.6841
| -9.2654
| -0.0505
|
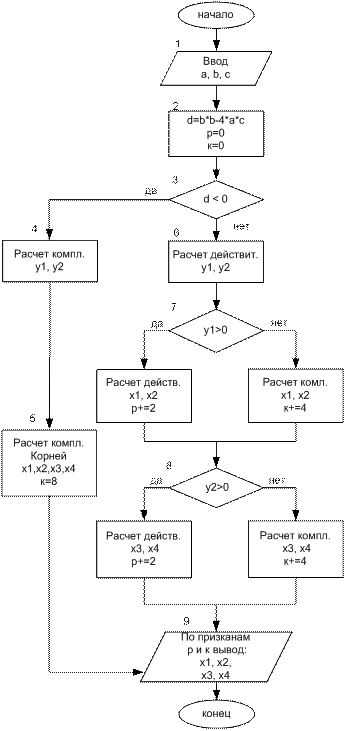
| Алгоритм решения биквадратного уравнения:
нахождение действительных и комплексных корней уравнения типа ax4 + bx2 + c = 0.
| Входные данные: a, b, c – коэффициенты биквадратного уравнения – тип double.
Выходные данные: тип double
х1, х2, х3, х4 – действительные корни биквадратного уравнения или комплексные числа, или их сочетание.
Вспомогательные переменные: переменная d, где будет храниться дискриминант квадратного уравнения тип double,
y1 y2 - дискриминанты квадратного уравнения тип double,
р – количество памяти для действительных корней int;
к – количество памяти для комплексных корней int.
Этапы решения:
1. Ввод коэффициентов a, b, c.
2. Вычисление дискриминанта по формуле d = b2-4ac.
3. Проверка знака дискриминанта.
4. Если d<=0, то корни комплексные: y1 + jy2 и y1 - jy2. При этом действительная часть комплексного числа равна 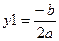 , мнимая часть числа равна , мнимая часть числа равна  .
5. Расчет х1,х2,х3,х4 – комплексов.
к=8.(4 корня по 2 элемента на корень).
6. Если d>=0, то корни действительные .
5. Расчет х1,х2,х3,х4 – комплексов.
к=8.(4 корня по 2 элемента на корень).
6. Если d>=0, то корни действительные  , , 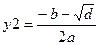 ,
7,8 . Проверка у1 и у2 на знак и вычисление соответствующих корней
х1 и х2 и х3, х4 (действительных или комплексных).
Если у1 и у2 >=0, вычисляются действительные корни х1 = ,
7,8 . Проверка у1 и у2 на знак и вычисление соответствующих корней
х1 и х2 и х3, х4 (действительных или комплексных).
Если у1 и у2 >=0, вычисляются действительные корни х1 =  , х2=-х1, х3= , х2=-х1, х3=  , х4=-х3; При этом к=0 р=4 (4 корня по 1-му значению)
Если только у1 или у2 >=0, то вычисляется два действительных корня, остальные два корня вычисляются из комплексного числа.
р=2 (2 корня по 1 элементу),
к=4 (2 корня по 2 элементам)
9 Вывод на экран ответа.
Общий объем памяти по четырем корням варьируется от 4 до 8 элементов типа double. , х4=-х3; При этом к=0 р=4 (4 корня по 1-му значению)
Если только у1 или у2 >=0, то вычисляется два действительных корня, остальные два корня вычисляются из комплексного числа.
р=2 (2 корня по 1 элементу),
к=4 (2 корня по 2 элементам)
9 Вывод на экран ответа.
Общий объем памяти по четырем корням варьируется от 4 до 8 элементов типа double.
|  Примечание:
Если при d<=0, то корни вычисляются из комплексных чисел Примечание:
Если при d<=0, то корни вычисляются из комплексных чисел  .
Извлечение корня из комплексного числа
- модуль .
Извлечение корня из комплексного числа
- модуль  ;
- угол ;
- угол 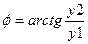 ;
- корень х3,4 либо ;
- корень х3,4 либо  . .
| Написать программу решения биквадратного уравнения по заданному алгоритму в консольном приложении.
Текст программы должен быть прокомментирован.
Примерный интерфейс программы:
Решение биквадратного уравнения: a*x^4 + b*x^2 + c = 0
Выполнил студент ХХХХ, группа ХХХ
Введите значение коэффициента а -> хх
Введите значение коэффициента b -> хх
Введите значение коэффициента c -> хх
Результаты вычислений - корни действительные/мнимые:
х1 = хх, х2 = хх, x3=xx, x4=xx
Протестировать программу на входных данных:
| вход
| выход
| | a
| b
| c
| x1
| x2
| x3
| x4
| | 0.1
|
|
| 0 + j4.1317
| 0 - j4.1317
| 0 + j1.7114
| 0 - j1.7114
| | -6
|
|
| -1.1424
| 1.1424
| 0 + j0.7991
| 0 - j0.7991
| | -2
|
| -10
| 3.4765
| -3.4765
| -0.6432
| 0.6432
|
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|














 Блок-схема цикла с параметром (for)
Блок-схема цикла с параметром (for)









 ,
,  , вывод на экран ответа.
Если d<=0, то корни комплексные: х1 ± ix2. При этом х1 – действительная часть комплексного числа, равная
, вывод на экран ответа.
Если d<=0, то корни комплексные: х1 ± ix2. При этом х1 – действительная часть комплексного числа, равная  , х2 – мнимая часть числа, равная
, х2 – мнимая часть числа, равная  . Вывод на экран ответа.
. Вывод на экран ответа.

 и
и  .
4. Рассчитать число корней приведенного уравнения (зависит от дискриминанта D).
.
4. Рассчитать число корней приведенного уравнения (зависит от дискриминанта D).
 5. Проанализировать дискриминант.
6. При отрицательном дискриминанте будут три действительные корня. Чтобы их рассчитать, надо воспользоваться формулами:
5. Проанализировать дискриминант.
6. При отрицательном дискриминанте будут три действительные корня. Чтобы их рассчитать, надо воспользоваться формулами:
 и
и  7. Произвести расчет х1, х2, х3:
7. Произвести расчет х1, х2, х3:

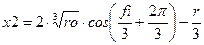
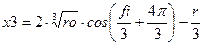 8. Вывести результаты х1, х2, х3.
9. При положительном дискриминанте будут три корня (один – действительный, два – комплексных). Чтобы их рассчитать, надо воспользоваться формулами Кардано (подстановка):
- если выражение
8. Вывести результаты х1, х2, х3.
9. При положительном дискриминанте будут три корня (один – действительный, два – комплексных). Чтобы их рассчитать, надо воспользоваться формулами Кардано (подстановка):
- если выражение  , то
, то
 и
и  ;
- если выражение
;
- если выражение  , то
, то
 и
и  При помощи этих выражений получить:
- действительный корень
При помощи этих выражений получить:
- действительный корень  ;
- комплексные корни, где
;
- комплексные корни, где

 и
и 
 .
10 Вывести x1,
.
10 Вывести x1, 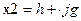 ,
, 
 Примечания:
1. использовать математические функции – cos, acos, sqrt, pow, fabs, которые находятся в библиотеке math.h
1 при вычислении
Примечания:
1. использовать математические функции – cos, acos, sqrt, pow, fabs, которые находятся в библиотеке math.h
1 при вычислении  необходимо сделать приведение типов – sqrt((double)3)
2. при вычислении
необходимо сделать приведение типов – sqrt((double)3)
2. при вычислении  необходимо сделать приведение типов pow((…..),(double)1/3));
3. j (i) – признак мнимой части комплексного числа, нужен только для формирования вывода в задаче.
необходимо сделать приведение типов pow((…..),(double)1/3));
3. j (i) – признак мнимой части комплексного числа, нужен только для формирования вывода в задаче.
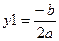 , мнимая часть числа равна
, мнимая часть числа равна  .
5. Расчет х1,х2,х3,х4 – комплексов.
к=8.(4 корня по 2 элемента на корень).
6. Если d>=0, то корни действительные
.
5. Расчет х1,х2,х3,х4 – комплексов.
к=8.(4 корня по 2 элемента на корень).
6. Если d>=0, то корни действительные  ,
, 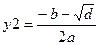 ,
7,8 . Проверка у1 и у2 на знак и вычисление соответствующих корней
х1 и х2 и х3, х4 (действительных или комплексных).
Если у1 и у2 >=0, вычисляются действительные корни х1 =
,
7,8 . Проверка у1 и у2 на знак и вычисление соответствующих корней
х1 и х2 и х3, х4 (действительных или комплексных).
Если у1 и у2 >=0, вычисляются действительные корни х1 =  , х2=-х1, х3=
, х2=-х1, х3=  , х4=-х3; При этом к=0 р=4 (4 корня по 1-му значению)
Если только у1 или у2 >=0, то вычисляется два действительных корня, остальные два корня вычисляются из комплексного числа.
р=2 (2 корня по 1 элементу),
к=4 (2 корня по 2 элементам)
9 Вывод на экран ответа.
Общий объем памяти по четырем корням варьируется от 4 до 8 элементов типа double.
, х4=-х3; При этом к=0 р=4 (4 корня по 1-му значению)
Если только у1 или у2 >=0, то вычисляется два действительных корня, остальные два корня вычисляются из комплексного числа.
р=2 (2 корня по 1 элементу),
к=4 (2 корня по 2 элементам)
9 Вывод на экран ответа.
Общий объем памяти по четырем корням варьируется от 4 до 8 элементов типа double.
 Примечание:
Если при d<=0, то корни вычисляются из комплексных чисел
Примечание:
Если при d<=0, то корни вычисляются из комплексных чисел  .
Извлечение корня из комплексного числа
- модуль
.
Извлечение корня из комплексного числа
- модуль  ;
- угол
;
- угол 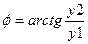 ;
- корень х3,4 либо
;
- корень х3,4 либо  .
.