
|
|
Детерминированные задачи и оптимизация решения в условиях неопределенности12 Задача, поставленная в предыдущем пункте, относится к числу типичных математических, так называемых вариационных задач. Методы решения таких задач хорошо разработаны в математике. Для нахождения максимума или минимума, короче, экстремума функции нужно продифференцировать ее по аргументу (или аргументам, если аргументов несколько), приравнять производные нулю и решить полученную систему уравнений. Однако, этот простой метод в задах исследования операций имеет ограниченное применение по нескольким причинам. Во-первых, когда аргументов Во-вторых, когда на элементы решения наложены ограничения (то есть область их изменения ограничена), часто экстремум наблюдается не в точке, где производные обращаются в нуль, а на границе области возможных решений. В-третьих, производных, о которых идет речь, может вообще не существовать, например, если аргументы изменяются не непрерывно, а дискретно, или же сама целевая функция имеет особенности. Таким образом, общих математических методов нахождения экстремумов функций любого вида при наличии произвольных ограничений не существует. Однако для случаев, когда функция и ограничения обладают определенными свойствами, имеются специальные методы. Например, если показатель эффективности зависит от элементов решения линейно и ограничения, наложенные на решение, также имеют линейный вид, максимум целевой функции находится с помощью специального математического метода – линейного программирования. В предыдущем пункте мы рассмотрели самый простой случай, когда все условия операции Гораздо чаще встречается случай, когда не все условия, в которых будет проводиться операция, известны заранее. То есть некоторые из условий содержат элемент неопределенности. Например, успех операции может зависеть от метеоусловий, или от колебаний спроса и предложений, которые заранее неизвестны, или от поведения хитрого противника, действия которого непредсказуемы. В подобных случаях эффективность операции зависит уже не от двух, а от трех групп факторов: 1) условий выполнения операции 2) элементов решения 3) неизвестных условий или факторов Итак, показатель эффективности зависит от трех групп факторов:
Так как величина В случае выбора решения в условиях неопределенности ее формулируют следующим образом. При заданных условиях Если условия выполнения операции известны неполностью, мы не имеем возможности так успешно организовать ее, как могли бы, располагая большей информацией. Поэтому любое решение, принятое в условиях неопределенности, хуже решения, принятого во вполне определенной ситуации. Задачи о выборе решения в условиях неопределенности встречаются в жизни гораздо чаще детерминированных задач. Пусть, например, мы собираемся в поездку и берем с собой чемодан вполне определенного объема, причем вес чемодана не должен быть больше какого-либо значения (иначе его нельзя будет поднять) (условия Применяемые в таких задачах методы существенно зависят от того, какова природа неизвестных факторов и какими сведениями о них мы располагаем. Наиболее простым для расчетов является случай, когда неизвестные факторы представляют собой случайные величины (или случайные функции), о которых имеются (или могут быть получены) статистические данные, характеризующие их распределение. Такие задачи исследования операций называют стохастическими задачами. Например, пусть оптимизируется работа грузовой железнодорожной станции. Заранее неизвестны ни точные моменты прибытия поездов, ни количество вагонов в каждом из них. Все эти характеристики представляют собой случайные величины, закон распределения каждой из которых может быть определен по имеющимся данным методами математической статистики. Другой пример. В каждой военной операции присутствуют случайные факторы, связанные с рассеиванием снарядов, со случайностью моментов обнаружения целей и т.д. Однако все эти факторы могут быть изучены методами теории вероятностей и для них могут быть получены законы распределения. В таких случаях показатель эффективности Первый способ – замена случайный факторов На практике так действительно часто поступают, заменяя случайные параметры (например, теплоемкость, индуктивность, коэффициент трения) их средними значениями. Например, при составлении плана снабжения группы предприятий сырьем можно пренебречь случайностью фактической производительности заводов-источников сырья, если производство стабильно налажено. Так делать нельзя, если влияние случайности на интересующий нас исход операции существенно. Например, пусть мы ведем обстрел какой-либо цели, стремясь попасть в нее. Производится несколько выстрелов. Заменим все случайные координаты точек попадания их математическим ожиданием – центром цели. Получится, что любой выстрел с гарантией попадает в цель. Таким образом, встречаются задачи с неопределенностью, которые нельзя свести к детерминированным. Второй способ – «оптимизация в среднем». Пусть показатель эффективности существенно зависит от случайных факторов
Элемент неопределенности при этом сохраняется. Успешность каждой отдельной операции может сильно отличаться от ожидаемой средней, как в большую, так и в меньшую стороны. При многократном выполнении операции показатели будут сглаживаться, стремиться к средним. Этот прием оправдан, если операция обладает свойством повторяемости. (Например, если мы предпринимаем ряд однородных операций с целью получения максимального дохода, то доходы от отдельных операций суммируются и «минус» в одном случае покрывается «плюсом» в другом.) Если речь идет об единичной, уникальной операции, то таким приемом пользоваться нельзя. Какой смысл в том, что операция в среднем приносит большой выигрыш, если в данном, единичном случае она может полностью разорить? В таких случаях можно ввести некоторое стохастическое ограничение, например, потребовать, чтобы вероятность выигрыша была не менее какого-то наперед заданного большого значения (0.99 или 0.995):
Введение такого ограничения означает, что из области возможных решений исключаются решения, ему не удовлетворяющие. Наличие таких ограничений усложняет задачу оптимизации. Кроме того для оценки эффективности операций, сильно зависящих от случайных параметров, можно определять помимо математического показателя эффективности также и его дисперсию (то есть разброс). Наиболее трудным для исследования является тот случай неопределенности, когда неизвестные факторы не могут быть изучены или описаны с помощью статистических методов. Их законы распределения или не могут быть получены, или, что еще хуже, их законов распределения вовсе не существует. Это бывает, когда рассматриваемое явление не обладает свойством статистической устойчивости. (Например, мы знаем, что некоторых планетах возможно наличие органической жизни, но совершенно невозможно подсчитать эту вероятность на основе каких-либо статистических данных. Пример про длину юбок. Пример про военные действия ответные действия противника. Очевидно, нет никакой возможности подсчитать вероятности этих гипотез.) В подобных случаях вместо произвольного и субъективного назначения вероятностей с дальнейшей оптимизацией в среднем, рекомендуется рассмотреть весь диапазон возможных условий 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 много (а это типично для задач исследования операций), совместное решение системы уравнений, полученных дифференцированием основной зависимости, часто оказывается не проще, а сложнее, чем непосредственный поиск экстремума.
много (а это типично для задач исследования операций), совместное решение системы уравнений, полученных дифференцированием основной зависимости, часто оказывается не проще, а сложнее, чем непосредственный поиск экстремума.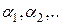 известны, и любой выбор решения
известны, и любой выбор решения 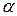 ;
; , которое предстоит выбрать;
, которое предстоит выбрать; . (будем обозначать их все одной буквой –
. (будем обозначать их все одной буквой –  ).
).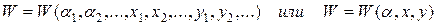
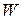 зависит от неизвестных факторов
зависит от неизвестных факторов  , которое, по возможности, обеспечивает максимальное значение показателя эффективности
, которое, по возможности, обеспечивает максимальное значение показателя эффективности 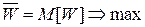 .
. .
.