|
|
Самоорганизующиеся системы на поверхностиВ дальнейшем изложении нам не понадобится такое детализированное и, следовательно, ограниченное понятие, как автомат. Мы будем пользоваться понятием «самоорганизующаяся система». Такой системой мы будем называть устройство, удовлетворяющее следующим чрезвычайно общим требованиям: 1. Имеется некоторый «идеальный» и неизменный проект системы. 2. Система может быть уклонена от состояния, соответствующего идеальному проекту (мы будем говорить, что система приобретает «диссонанс»). 3. Система совершает действия по уменьшению собственного диссонанса. 4. Системе не требуется питание энергией. На строение системы ограничения не накладываются. Ее можно рассматривать и как дискретное, и как непрерывное образование. Пусть на каждой стороне некоторой двусторонней поверхности функционирует по самоорганизующейся системе. Пусть элементы, из которых составлены обе эти системы и которые они должны организовывать, имеют «два лица», т.е. на одной стороне данная «морфологическая» единица выполняет одну функцию, а на другой—другую, и пусть эти функции «равномерно перепутаны». Элементы, организованные на одной стороне, будут выглядеть как случайное нагромождение для системы, находящейся на другой стороне, и поэтому эта другая система начнет организовывать элементы, иначе говоря, она начнет уменьшать свой диссонанс и, тем самым, в принципе, разрушать структуру, находящуюся на противоположной стороне, т.е. увеличивать ее диссонанс. Подчеркнем, что фактом задания «двух лиц» одной и той же совокупности морфологических единиц Мы создали возможность построить две различные по своему функционированию системы, выполненные в одном «морфологическом теле». Поскольку никаких ограничений на характер поверхности мы не накладываем, процессы самоорганизации можно рассматривать как протекающие на внешней и внутренней сторонах сферы. Теперь сделаем следующий шаг. Введем четырехмерное евклидово пространство, построим в нем четырехмерную сферу, и отождествим ее с «обычным» трехмерным пространством (правомерность этого отождествления мы не рассматриваем). Мы можем говорить о внешней и внутренней сторонах этой сферы. Поместим на каждый из двух сторон гиперсферы самоорганизующиеся системы, и пусть элементы, из которых они сложены, имеют также два «лица»: одно, обращенное внутрь гиперсферы, а другое—наружу. Мы как наблюдатели и компоненты самоорганизующейся системы принадлежим одной стороне поверхности. «Наша» организация выступает для нас в виде процессов уменьшения энтропии. Например, с «нашей» точки зрения газ представляет собой хаотическое движение молекул с очень низкой степенью организованности. С точки же зрения наблюдателя, «существующего» по другой нормали, «тот же» газ является высокоорганизованной материей (например, живым организмом!), тогда как наши тела представляются ему высокоэнтропийным газом. Правила взаимодействия антиподов Правила мы подобрали специально такими, чтобы процесс, порожденный их реализацией в нашей модели, мог бы интерпретироваться одновременно и как физическая, и как 'биологическая действительность. «Неживая природа» выступает как своеобразный вырожденный случай «живой природы». Пусть A-система—одна из систем, принадлежащих «нашей» стороне поверхности, В-система принадлежит противоположной стороне. В-систему изобразим на рисунке пунктиром (она как бы просвечивает через поверхность), A-систему ограничим четким контуром (рис. 54). Обе системы могут совершать «ходы». Под ходом понимается действие системы по изменению собственного диссонанса. При этом имеется в виду не только некоторое единичное «подсоединение» детали или улучшение ее позиции, а целый комплекс одновременных актов, суммарный результат которых изменяет диссонанс системы. Они могут происходить одновременно в разных точках пространства.
Единицей взаимодействия самоорганизующихся систем является такт. Такт состоит из двух ходов. Введем два типа тактов: в такте первого типа первый ход делает А-система, в такте второго типа—В-система. При взаимодействии систем в такте должны выполняться следующие два правила: 1) сторона, делающая первый ход в такте, не может нанести ущерба другой стороне, т.е. сторона, имеющая преимущество хода, не может улучшить свою структуру за счет увеличения диссонанса другой стороны; 2) сторона, делающая второй ход в такте, не может свести на нет улучшение организации, полученное другой стороной в результате первого хода. Будем полагать, что В-система «объемлет» А-систему, т.е. А-система находится внутри «просвечивающего» контура В-системы. Контур системы отделяет ту часть «морфологического поля», изменение конфигурации которого изменяет диссонанс системы. Мы будем предполагать, что если произошло изменение конфигурации части «морфологического поля», общей для А и В, и при этом диссонанс одной из систем уменьшился на величину Q, то диссонанс другой возрос на ту же величину Q (отметим, что возможно построение модели с иным соотношением между диссонансами противостоящих систем). Мы задаем некоторую неформализованную игру. Такт первого типа Изменения организованности системы изобразим векторами: векторы, идущие вверх, будут изображать организованность, приобретенную «нашей» стороной, т.е. А-системой, а векторы, идущие вниз—приобретение организованности В-системой. Пусть Л-система желает уменьшить свой диссонанс на величину Q. Для этого она должна была бы сделать ход, который изобразится вектором Q. При этом диссонанс В-системы увеличился 124 бы на величину Q, т.е. А-система нанесла бы В-системе ущерб в Q единиц организованности. Однако это запрещено правилом 1. Поэтому одновременно с действием увеличения своей организованности А-система должна на такую же величину, но за счет действия в другой точке, улучшить организованность В-системы, т.е. в некоторой точке вне своих границ произвести разрушение «материи» своего типа, чтобы в результате В-система
Вторым ходом в такте первого типа В-система может совершить действия, несколько ухудшающие приобретенную А-системой организацию (рис. 56), но не нарушить правило 2. Физическая интерпретация такта первого типа. Пусть А-система желает построить дом. Почему система не может взять и «просто» построить?! Зачем для того, чтобы совершить это действие, ей требуется сжигать бензин? Дело в том, что строя дом, она наносит ущерб В-системе. Она может построить дом лишь в том случае, если возместит ущерб, нанесенный В-системе. И она возмещает этот ущерб, приводя бензин в более организованное, с точки зрения В-системы, состояние. (Интуитивно ощущается, что точнее было бы сказать, что А-система разрешает В-системе, в некоторой области, вне своих границ, улучшить свою организацию. Однако рассуждение такого рода требует некоторого усложнения исходной модели.) Правда, возникает вопрос: почему нельзя жечь бензин в одном месте и тем самым получать право строить дом в совершенно другом, никак с тем местом не связанным? По-видимому, дело заключается в необходимости жесткой синхронизации «приобретения» и «компенсации». Для исследователя, находящегося в А-системе, явления будут протекать так, как их «видит» современная физика: разрушилась одна структура (бензин) — возникла другая (дом). Такой исследователь интерпретирует это явление как перенос энергии. С точки же зрения исследователя, который выделял обе организации, понятия энергии и ее переноса не имеют смысла. Он просто фиксирует, что А-система совершила ход, разрешенный правилами. Для него разрушение структуры в одном месте и возникновение в другом — это два рядом лежащих явления, не связанные причинной связью. Далее B-система может улучшить свою структуру, но так, чтобы 'выполнялось правило 2. B-система улучшает структуру бензина еще дополнительно, и поэтому его сгорает больше, чем требуется для компенсации. Такт второго типа
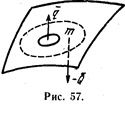
Первый ход делает B-система. Она улучшает свою организацию вне границ A-системы. Очевидно, что улучшить ее внутри границ A-системы B-система не может, ибо в этом случае она нарушает правило 1. A-система имеет право на ответный ход, и она улучшает свою структуру в рамках правила 2 (рис. 57). Физическая интерпретация такта второго типа. B-система разрушает «нашу» материю Солнца, тем самым улучшая свою организацию. Разрушая Солнце, она не разрушает цветок Подсолнечника. Подсолнечник «имеет право» улучшить свою организацию, не нарушая правило 2. Наблюдатель, принадлежащий к той же ветви организации, что и Подсолнечник, зафиксирует перенос энергии. «Универсальный наблюдатель» зафиксирует такт игры двух самоорганизующихся систем, совершенный по правилам. Многие энергетические явления могут быть интерпретированы как суперпозиции очень «мелких» тактов. Заметим, что правила взаимодействия не дают преимущества ни одной из сторон. Некоторые преимущества B-системы являются следствием того, что B-еистема объемлет A-систему. Это преимущество феноменологически фиксируется вторым началом термодинамики. (Разумеется, лишь в рамках нашей модели!). Очевидно, что допустим случай, когда A-система объемлет B-систему. Возможно, что живые организмы представляют собой пример взаимодействия при подобном «обратном» отношении «объемлемости» (может быть, это позволит объяснить невыполнение теоремы Пригожина для эмбриогенеза живых организмов, на которое указывает К. С. Тринчер? [31]). Вполне допустимо, что можно построить иную процедуру взаимодействия, которая окажется более эффективной для объяснения «энергетических явлений». Введенная нами конструкция в основном должна проиллюстрировать возможности моделей такого типа. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 приобрела организованность Q. Совокупность этих двух действий и будет ходом А-системы (рис. 55).
приобрела организованность Q. Совокупность этих двух действий и будет ходом А-системы (рис. 55).