
|
|
Вероятность отказа. Относительная и абсолютная пропускная способности. Среднее число занятых каналов.12 Отказ в обслуживании заявки происходит, когда все m мест в очереди заняты, т.е.:
Относительная пропускная способность равна:
Абсолютная пропускная способность:
Среднее число занятых каналов
21. Многоканальная СМО с ожиданием Система с ограниченной длиной очереди. Рассмотрим Состояния системы нумеруются по числу заявок, связанных системой: нет очереди:
есть очередь:
У каждой стрелки проставлены соответствующие интенсивности потоков событий. По стрелкам слева направо систему переводит всегда один и тот же поток заявок с интенсивностью
Среднее число занятых каналов. Для СМО с очередью среднее число занятых каналов не совпадает со средним числом заявок, находящихся в системе: последняя величина отличается от первой на среднее число заявок, находящихся в очереди. Обозначим среднее число занятых каналов
Среднее число заявок в очереди можно вычислить непосредственно как математическое ожидание дискретной случайной величины:
где Здесь опять (выражение в скобках) встречается производная суммы геометрической прогрессии используя соотношение для нее, получаем:
Среднее число заявок в системе:
22.Среднее время ожидания заявки в очереди. Рассмотрим ряд ситуаций, различающихся тем, в каком состоянии застанет систему вновь пришедшая заявка и сколько времени ей придется ждать обслуживания. Если заявка застанет не все каналы занятыми, ей вообще не придется ждать (соответствующие члены в математическом ожидании равны нулю). Если заявка придет в момент, когда заняты все п каналов, а очереди нет, ей придется ждать в среднем время, равное
Так же, как и в случае одноканальной СМО с ожиданием, отметим, что это выражение отличается от выражения для средней длины очереди (5.59) только множителем
Среднее время пребывания заявки в системе, так же, как и для одноканальной СМО, отличается от среднего времени ожидания на среднее время обслуживания, умноженное на относительную пропускную способность:
23/24.Системы с неограниченной длиной очереди. Мы рассмотрели Так же, как и ранее, при анализе систем без ограничений необходимо рассмотреть полученные соотношения при Вероятности состояний получим из формул предельным переходом (при
Вероятность отказа, относительная и абсолютная пропускная способность. Так как каждая заявка рано или поздно будет обслужена, то характеристики пропускной способности СМО составят:
Среднее число заявок в очереди получим при
асреднее время ожидания — из (5.60):
Среднее число занятых каналов
Среднее число заявок, связанных с СМО, определяется как среднее число заявок в очереди плюс среднее число заявок, находящихся под обслуживанием (среднее число занятых каналов):
СМО с ограниченным временем ожидания. Ранее рассматривались системы с ожиданием, ограниченным только длиной очереди (числом m заявок, одновременно находящихся в очереди). В такой СМО заявка, раз ставшая в очередь, не покидает ее, пока не дождется обслуживания. На практике встречаются СМО другого типа, в которых заявка, подождав некоторое время, может уйти из очереди (так называемые «нетерпеливые» заявки). Рассмотрим СМО подобного типа, предполагая, что ограничение времени ожидания является случайной величиной. Предположим, что имеется n-канальная СМО с ожиданием, в которой число мест в очереди не ограничено, но время пребывания заявки в очереди является некоторой случайной величиной со средним значением
Если этот поток пуассоновский, то процесс, протекающий в СМО, будет марковским. Найдем для него вероятности состояний. Нумерация состояний системы связывается с числом заявок в системе — как обслуживаемых, так и стоящих в очереди: нет очереди:
Граф состояний и переходов системы показан на рис. 5.10.
Разметим этот граф, как и раньше; у всех стрелок, ведущих слева направо, будет стоять интенсивность потока заявок Как видно из графа, имеет место схема размножения и гибели; применяя общие выражения для предельных вероятностей состояний в этой схеме (используя сокращенные обозначения
Отметим некоторые особенности СМО с ограниченным ожиданием сравнительно с ранее рассмотренными СМО с «терпеливыми» заявками. Если длина очереди не ограничена и заявки «терпеливы» (не уходят из очереди), то стационарный предельный режим существует только в случае Напротив, в СМО с «нетерпеливыми» заявками, уходящими рано или поздно из очереди, установившийся режим обслуживания при Для СМО с «нетерпеливыми» заявками понятие «вероятность отказа» не имеет смысла — каждая заявка становится в очередь, но может и не дождаться обслуживания, уйдя раньше времени. Относительная пропускная способность, среднее число заявок в очереди. Относительную пропускную способность q такой СМО можно подсчитать следующим образом. Очевидно, обслужены будут все заявки, кроме тех, которые уйдут из очереди досрочно. Подсчитаем, какое в среднем число заявок покидает очередь досрочно. Для этого вычислим среднее число заявок в очереди:
На каждую из этих заявок действует «поток уходов» с интенсивностью
заявок. Относительная пропускная способность СМО будет составлять:
Среднее число занятых каналов
Среднее число заявок в очереди. Соотношение (5.64) позволяет вычислить среднее число заявок в очереди
а входящее в эту формулу среднее число занятых каналов можно найти как математическое ожидание случайной величины Z, принимающей значения 0, 1, 2, ..., n с вероятностями
25. Игры с противоположными интересами. Основные понятия. Платежная матрица. Ситуация, в которой сталкиваются две или более сторон, преследующие различные цели, называется конфликтной. Одним из подходов к реализации оптимизационной мат. модели в условиях неопределенности, когда возникает конфликтная ситуация, является теорией игр. Игра-мероприятие, состоящее из ряда действий сторон. Правила игры есть совокупность системы условий, регламентирующих возможные варианты действий сторон, объема информации у каждой стороны о поведении другой, результатов, к которым приводят набор возможных вариантов действий. Игра состоит из ряда последовательных ходов. Ход-есть выбор одного действия из предусмотренных правилами набора действий. Стороны, участвующие в конфликте наз. игроками, а исход конфликта-проигрышем(выигрышем). Стратегией наз. совокупность правил, определяющих выбор варианта при каждом ходе. Оптимальной наз. стратегия, которая при многократном повторении игры обеспечивает данной стороне максимально возможный средний выигрыш. Стратегические игры моделируют конфликтные ситуации, в которых действуют не менее двух сторон, каждая из которых выступает со своими вариантами действий. Нестратегические игры моделируют конфликтные ситуации, когда либо действует одна сторона, либо существует коалиция сторон, все участники которой выступают с одним набором вариантов действий. Игра называется парной, если в ней участвуют ровно 2 игрока и множественной, если число игроков больше двух. Парная стратегия является антагонистической, если цели сторон прямопротивоположны. В этом случае выигрыш одного игрока является проигрышем другого. Конечные стратегии игры описывают конфликтную ситуацию, в которой все стороны имеют конечное число возможных вариантов действий. Если хотя бы одна сторона имеет бесконечное число вариантов, игра относится к классу бесконечных. При одноходовой игре, любая из сторон имеет по одному ходу. При многоходовой, делается более двух ходов. Матричной игрой наз. стратегическая парная антагонистическая одноходовая игра с конечным числом вариантов действий у каждой из сторон. Платежная матрица- статистический метод принятия решения, помогающий руководителю выбирать из возможных альтернатив.
26. Нижняя и верхняя цена игры. Принцип минимакса. В основе решения матричной игры лежит принцип минимакса или максимина, который состоит в том, что одна сторона оценивает целесообразность применения любой из своих стратегий, исходит из возможности наиболее неблагоприятного для себя ответного хода другой стороны. Выбранная таким образом стратегия гарантирует одной стороне максимально возможный выигрыш (А) при самой неблагоприятной для него стратегии для любой стороны. А: оценивает для каждой своей стратегии минимально возможный выигрыш αij.. αi= min αij i=1,m βj= max αij j=1,n α= max αi i=1,m α= max min αij i=1,m, j=1,n –нижняя цена игры β= min max αij i=1,m, j=1,n –верхняя цена игры Стратегия игрока А, доставляющая максимальный выигрыш, называется максимальной стратегией. Стратегия В, доставляющая минимальной проигрыш, называется минимальной стратегией. Величина υ=α=β наз. чистой ценой игры. 27. Игры с седловой точкой. Элемент платежной матрицы, являющийся одновременно минимальным в своей строке и максимальным в своем столбце, наз. седловой точкой. При наличии у игры седловой точкой, любая из сторон, уклонившаяся от стратегии, выбранной в соответствии с принципом минимакса, обязательно потеряет эффективность, если только другая сторона придерживается при этом своей стратегии. Подобная ситуация наз. ситуацией равновесия. При наличии седловой точки, решением игры является пара оптимальной стратегии (A*ij, B*ij), соответствующая этой точке. Совокупность оптимальных стратегий наз. решением игры чистых стратегий. Св-ва: 1. Если А выбрал оптим. стратегию, то независимо от стратегии В, его выигрыш будет не меньше чистой цены игры. 2. Если В выбрал оптим. стратегию, то какой бы стратегии не придерживался бы А, выигрыш В не превысит чистой цены игры. 28. Решение игры в смешанных стратегиях. Активные стратегии. Теорема об активных стратегиях. Рассмотрим α ≠β, α<β, α<υ<β. В случае, если α ≠β, то у такой игры нет седловой точки В этом случае принцип минимакса или максимина не подходит. (Решение игр 2х2) Смешанные стратегии предполагают, что каждый игрок будет выбирать случайные из возможно допустимых чистых стратегий, либо частично реализовывать чистые стратегии в заданных пропорциях. Активными называются те стратегии, которые доминируют над другими. Рассмотрим игру 2хn Наносим на оси цену игрока В. Из самой высокой точки опускаем перпендикуляр. Самая высокая точка нижней ломаной является точкой пересечения прямых, соответствующих активным стратегиям В*1 и В*2.
Таким образом исходная игра сокращается до игры 2х2. Решаем игру и находим вероятности активных стратегий. Вероятности активных стратегий. Вероятности пассивных стратегий приравниваем к нулю. 36. Игра 2*2.Аналитический и графический способы решения.
В общем случае игра 2 Прежде всего необходимо проверить, есть ли у данной игры седловая точка. Если да, то игра имеет решение в чистых стратегиях, причём оптимальными стратегиями игроков 1 и 2 соответственно будут чистая максиминная и чистая минимаксная стратегии. Если же игра с матрицей выигрышей А не имеет чистых стратегий, то оба игрока имеют только такие оптимальные стратегии, которые используют все свои чистые стратегии с положительными вероятностями. В противном случае один из игроков (например 1) имеет чистую оптимальную стратегию, а другой – только смешанные. Не ограничивая общности, можно считать, что оптимальной стратегией игрока 1 является выбор с вероятностью 1 первой строки. Далее, по свойству 1 следует, что а11 = а12 = и матрица имеет вид Легко видеть, что для матриц такого вида одна из стратегий игрока 2 является доминируемой. Следовательно, по свойству 4 этот игрок имеет чистую стратегию, что противоречит предположению. Пусть Х = (, 1 ) – оптимальная стратегия игрока 1. Так как игрок 2 имеет смешанную оптимальную стратегию, из свойства 1 получим, что (см. также свойство 7) Отсюда следует, что при 0 столбцы матрицы А не могут быть пропорциональны с коэффициентом пропорциональности, отличным от единицы. Если же коэффициент пропорциональности равен единице, то матрица А принимает вид и игрок 1 имеет чистую оптимальную стратегию (он выбирает с вероятностью 1 ту из строк, элементы которой не меньше соответствующих элементов другой), что противоречит предположению. Следовательно, если 0 и игроки имеют только смешанные оптимальные стратегии, то определитель матрицы А отличен от нуля. Из этого следует, что последняя система уравнений имеет единственное решение. Решая её, находим Аналогичные рассуждения приводят нас к тому, что оптимальная стратегия игрока 2 Y = (, 1 - ) удовлетворяет системе уравнений откуда
Графический метод применим к играм, в которых хотя бы один игрок имеет только две стратегии. Первый случай. Рассмотрим игру (2х2) с матрицей Решением игры являются смешанные стратегии игроков х1 - вероятность применения первым игроком первой стратегии, х2 - вероятность применения первым игроком второй стратегии, у1 - вероятность применения вторым игроком первой стратегии, у2 - вероятность применения вторым игроком второй стратегии. Очевидно, что
Найдем решение игры графическим методом (рис.1).
Рис. 1.
На оси ОХ отложим отрезок, длина которого равна единице. Левый конец (х = 0) соответствует стратегии первого игрока А1, правый Внутренние точки отрезка будут соответствовать смешанным стратегиям Через концы отрезка проведем прямые, перпендикулярные оси ОХ, на которых будем откладывать выигрыш при соответствующих чистых стратегиях. Если игрок В применяет стратегию В1, то выигрыш при использовании первым игроком стратегий А1 и А2 составит соответственно а11 и а21. Отложим эти точки на прямых и соединим их отрезком В1В1. Если игрок А применяет смешанную стратегию, то выигрышу соответствует некоторая точка М, лежащая на этом отрезке. Аналогично строится отрезок В2В2, соответствующий стратегии В2 игрока В.
Определение 20. Ломаная линия, составленная из частей отрезков, интерпретирующих стратегии игрока В, расположенная ниже всех отрезков, называется нижней границей выигрыша, получаемого игроком А. Определение 21.Стратегии, части которых образуют нижнюю границу выигрыша, называются активными стратегиями.
В игре (2х2) обе стратегии являются активными. Ломаная В1КВ2 является нижней границей выигрыша (рис. 2), получаемого игроком А. Точка К, в которой он максимален, определяет цену игры и ее решение.
Рис. 2.
Найдем оптимальную стратегию первого игрока. Запишем систему уравнений
Приравнивая выражения для v из уравнений системы и учитывая, что
Составляя аналогичную систему
и учитывая условие можно найти оптимальную стратегию игрока В:
Если игра 2xn или mx2 не является игрой в чистых стратегиях, то необходимо попытаться уменьшить размер игры за счет дублирования и доминирования. Если же это не удается, то с помощью графо-аналитического метода выявить активные стратегии. Замечание. Активной стратегией называются те стратегии, которые доминируют над другими(те, которые останутся после сокращения) Рассмотрим игру 2xn
Самая высокая точка нижней ломаной является точкой пересечения прямых, соотв. активным стратегиям данной игры. В1* В1*(. Вi* Вj*) Таким образом исх игра сокращается до исходной игры вида:
Решаем игру 2х2 и находим вероятности активых стратегий. Вероятностям пассивных стратегий присваиваем нули.
Рассмотрим игру mx2
Не меняя общности будем считать, что в данной платежн. Матрице нет дублирования и доминирования. Для выявления активных стратегий игрока А применим тот же подход, что и ранее описанный, т.е.
Нижняя точка верхней ломаной соответствует активным стратегиям ai и aj. После этого задача сводится к размеру 2х2 и решается способом упомянутом выше.
38. игры m x n сведение решения игры m x n к задаче линейного програмирования. Основная теорема теории игр.
Игра размера mxn не имеет наглядной геометрической интерпретации. Ее решение достаточно трудоемко, но принципиальных трудностей не имеет, поскольку может быть сведено к решению задаче линейного программирования. Наряду с приводимыми выше теоремой Неймана и теоремой об активных стратегиях справедлива следующая терема теории игр.
Теорема. Для того чтобы число v было ценой игры, а U* и Z*- оптимальными стратегиями, необходимо и достаточно выполнение неравенств:
Рассмотрим игру mxn, определяемую матрицей:
Как и ранее, игрок A обладает стратегиями A1, A2, ..., Am, игрок В – стратегиями B1, B2, …, Bn. Требуется определить оптимальные стратегии игроков U* и Z*. Рассмотрим оптимальную стратегию U* игрока A. Согласно теореме, приведенной выше, справедливо следующее утверждение. Если игрок А применяет смешанную стратегию U* = ( Для оптимальной стратегии U* все средние выигрыши не меньше цены игры v, поэтому получаем систему неравенств:
Предположим для определенности, что v > 0. Этого всегда можно достигнуть благодаря тому, что прибавление ко всем элементам матрицы А одного и того же постоянного числа С не приводит к изменению оптимальных стратегий, а только лишь увеличивает цену игры на С. Каждое из неравенств разделим на число v (v > 0), а также введем новые переменные: y1 = Тогда система (5.3) примет вид:
При этом yi ≥ 0, Далее рассмотрим равенство Разделим неравенство на число v (v ≠ 0). Получим:
Вспомним, что цель игрока А – максимизировать свой гарантированный выигрыш, т.е. цену игры v. Максимизация цены игры v эквивалентна минимизации величины 1/v, поэтому задача может быть сформулирована следующим образом: определить значения переменных yi ≥ 0, i = 1, 2, …, m, так, чтобы они удовлетворяли линейным ограничениям (5.4) и при этом линейная функция (5.5) обращалась в минимум. Перед нами задача линейного программирования. Решая задачу (5.4) – (5.5), можно найти оптимальную стратегию U*.
Аналогичные рассуждения выполним и для игрока В. Обозначив xj =
Таким образом, задача определения оптимальной стратегии игрока В сводится к следующему: определить значения переменных xj ≥ 0, j = 1, 2, …, n, так, чтобы они удовлетворяли линейным ограничениям (5.6) и при этом линейная функция (5.7) обращалась в максимум. Решая задачу линейного программирования (5.6) – (5.7), получим оптимальную стратегию Z*.
Вновь приведем формулировки полученных задач линейного программирования.
Очевидно, что задачи (5.4) – (5.5) и (5.6) – (5.7) представляют собой пару взаимно двойственных задач линейного программирования. Их решение позволяет решить соответствующую игру. При этом:
Таким образом, процесс нахождения решения игры с использованием методов линейного программирования включает следующие этапы. 1. Формулировка пары двойственных задач линейного программирования, эквивалентных заданной парной игре. 2. Определение оптимальных планов двойственных задач. 3. Нахождение решения игры с использованием соотношений между оптимальными планами двойственных задач и оптимальными стратегиями и ценой игры (формулы (5.8)).

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|




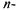 канальную СМО с ожиданием, на которую поступает поток заявок с интенсивностью
канальную СМО с ожиданием, на которую поступает поток заявок с интенсивностью 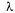 ; интенсивность обслуживания (для одного канала)
; интенсивность обслуживания (для одного канала)  ; число мест в очереди
; число мест в очереди  .
. —все каналы свободны;
—все каналы свободны; — занят один канал, остальные свободны;
— занят один канал, остальные свободны; — заняты
— заняты  каналов, остальные нет;
каналов, остальные нет;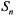 — заняты все
— заняты все  каналов, свободных нет;
каналов, свободных нет; —заняты все n каналов; одна заявка стоит в очереди;
—заняты все n каналов; одна заявка стоит в очереди; — заняты все n каналов, r заявок в очереди;
— заняты все n каналов, r заявок в очереди; —заняты все n каналов, r заявок в очереди.
—заняты все n каналов, r заявок в очереди.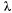 , по стрелкам справа налево систему переводит поток обслуживании, интенсивность которого равна
, по стрелкам справа налево систему переводит поток обслуживании, интенсивность которого равна  , умноженному на число занятых каналов.
, умноженному на число занятых каналов.
 . Каждый занятый канал обслуживает в среднем
. Каждый занятый канал обслуживает в среднем  заявок в единицу времени, а СМО в целом обслуживает в среднем А заявок в единицу времени. Разделив одно на другое, получим:
заявок в единицу времени, а СМО в целом обслуживает в среднем А заявок в единицу времени. Разделив одно на другое, получим:




 (потому что «поток освобождений»
(потому что «поток освобождений»  каналов имеет интенсивность
каналов имеет интенсивность  ). Если заявка застанет все каналы занятыми и одну заявку перед собой в очереди, ей придется в среднем ждать в течение времени
). Если заявка застанет все каналы занятыми и одну заявку перед собой в очереди, ей придется в среднем ждать в течение времени 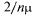 (по
(по  на каждую впереди стоящую заявку) и т. д. Если заявка застанет в очереди
на каждую впереди стоящую заявку) и т. д. Если заявка застанет в очереди  заявок, ей придется ждать в среднем в течение времени
заявок, ей придется ждать в среднем в течение времени  . Если вновь пришедшая заявка застанет в очереди уже m заявок, то она вообще не будет ждать (но и не будет обслужена). Среднее время ожидания найдем, умножая каждое из этих значений на соответствующие вероятности:
. Если вновь пришедшая заявка застанет в очереди уже m заявок, то она вообще не будет ждать (но и не будет обслужена). Среднее время ожидания найдем, умножая каждое из этих значений на соответствующие вероятности:
 , т. е.
, т. е.

 канальную СМО с ожиданием, когда в очереди одновременно могут находиться не более m заявок.
канальную СМО с ожиданием, когда в очереди одновременно могут находиться не более m заявок. .
. ). Заметим, что сумма соответствующей геометрической прогрессии сходится при
). Заметим, что сумма соответствующей геометрической прогрессии сходится при  и расходится при
и расходится при  > 1. Допустив, что
> 1. Допустив, что  < 1 и устремив в формулах (5.56) величину m к бесконечности, получим выражения для предельных вероятностей состояний:
< 1 и устремив в формулах (5.56) величину m к бесконечности, получим выражения для предельных вероятностей состояний:

 из (5.59):
из (5.59):

 , как и ранее, определяется через абсолютную пропускную способность:
, как и ранее, определяется через абсолютную пропускную способность:
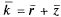
 , таким образом, на каждую заявку, стоящую в очереди, действует своего рода пуассоновский «поток уходов» с интенсивностью
, таким образом, на каждую заявку, стоящую в очереди, действует своего рода пуассоновский «поток уходов» с интенсивностью
 — все каналы свободны;
— все каналы свободны; —занят один канал;
—занят один канал; —заняты два канала;
—заняты два канала; —заняты все n каналов; есть очередь:
—заняты все n каналов; есть очередь: — заняты все n каналов, одна заявка стоит в очереди;
— заняты все n каналов, одна заявка стоит в очереди; — заняты все n каналов, r заявок стоят в очереди и т. д.
— заняты все n каналов, r заявок стоят в очереди и т. д.
 . Для состояний без очереди у стрелок, ведущих из них справа налево, будет, как и раньше, стоять суммарная интенсивность потока обслуживании всех занятых каналов. Что касается состояний с очередью, то у стрелок, ведущих из них справа налево, будет стоять суммарная интенсивность потока обслуживании всех n каналов
. Для состояний без очереди у стрелок, ведущих из них справа налево, будет, как и раньше, стоять суммарная интенсивность потока обслуживании всех занятых каналов. Что касается состояний с очередью, то у стрелок, ведущих из них справа налево, будет стоять суммарная интенсивность потока обслуживании всех n каналов  плюс соответствующая интенсивность потока уходов из очереди. Если в очереди стоят r заявок, то суммарная интенсивность потока уходов будет равна
плюс соответствующая интенсивность потока уходов из очереди. Если в очереди стоят r заявок, то суммарная интенсивность потока уходов будет равна 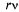
 , запишем:
, запишем:
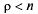 (присоответствующая
(присоответствующая  бесконечная геометрическая прогрессия расходится, что физически соответствует неограниченному росту очереди при
бесконечная геометрическая прогрессия расходится, что физически соответствует неограниченному росту очереди при  ).
). достигается всегда, независимо от приведенной интенсивности потока заявок
достигается всегда, независимо от приведенной интенсивности потока заявок  . Это следует из того, что ряд для
. Это следует из того, что ряд для  в знаменателе формулы сходится при любых положительных значениях
в знаменателе формулы сходится при любых положительных значениях 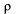 и
и  .
.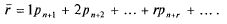
 . Значит, из среднего числа
. Значит, из среднего числа  заявок в очереди в среднем будет уходить, не дождавшись обслуживания,
заявок в очереди в среднем будет уходить, не дождавшись обслуживания,  заявок в единицу времени и всего в единицу времени в среднем будет обслуживаться
заявок в единицу времени и всего в единицу времени в среднем будет обслуживаться

 по-прежнему получаем, деля абсолютную пропускную способность А на
по-прежнему получаем, деля абсолютную пропускную способность А на  :
:
 , не суммируя бесконечного ряда (5.63). Из (5.64) получаем:
, не суммируя бесконечного ряда (5.63). Из (5.64) получаем:
 ,
,  :
:
 2 определяется матрицей
2 определяется матрицей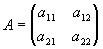
 .
.

 ;
; .
.
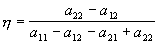 .
. без седловой точки.
без седловой точки. и
и  , где
, где




 получим
получим
 (1)
(1) (2)
(2)


 (3)
(3)

 aij
aij  ≥ v,
≥ v,  ,
,  aij
aij  ≤ v,
≤ v, 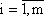 .
.

 .
.
 ,
,  , ...,
, ...,  ) против чистой стратегии Bj игрока В, то он получает средний выигрыш или математическое ожидание выигрыша aj = a1j
) против чистой стратегии Bj игрока В, то он получает средний выигрыш или математическое ожидание выигрыша aj = a1j 
 = y1 + y2 + ... + ym → min;
= y1 + y2 + ... + ym → min;
 = x1 + x2 + ... + xn → max;
= x1 + x2 + ... + xn → max;
 ;
;  ,
,  ,
,