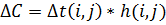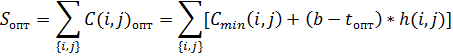|
|
Временные характеристики сетевых графиковХарактеристики событий: 1. Ранний срок наступления событий:
где Ранние сроки свершения событий вычисляются по сетевому графику слева направо по прямому ходу. 2. Поздний срок свершения событий:
Поздние сроки свершения событий вычисляются по сетевому графику справа налево по обратному ходу. 3. Резерв времени события: R(i) = Характеристики работ: 1. Ранний срок начала работы:
2. Ранний срок окончания работ:
3. Поздний срок окончания работы:
4. Поздний срок начала работы:
5. Полный резерв времени работ:
6. Частичный резерв времени первого вида:
7. Свободный резерв времени:
8. Независимый резерв времени работ:
9. Резерв времени пути: R(L) = Все резервы времени неотрицательны, вместо отрицательных величин используется ноль. 10. Проверка резервов
Для наглядности все временные характеристики можно представить в виде линейной диаграммы (Рис. 1.1.).
Рис. 1.1. Линейная диаграмма взаимосвязи временных характеристик. УПРАВЛЕНИЕ СЕТЕВЫМ ГРАФИКОМ Оптимизация сетевого графика Задачи оптимизации: 1. Сокращение стоимости проекта за счет перераспределения ресурсов; 2. Выравнивание коэффициентов напряженности для снижения вероятности срыва выполнения в заданные сроки; 3.Сокращение продолжительности критического пути за счет пересмотра продолжительности работ или пересмотра сетевого графика. Оптимизация представляет собой минимизацию или максимизацию параметров сетевого графика, например, времени или стоимости проекта. Методы решения задач в оптимизации: 1.Перераспределение ресурсов (временных, трудовых, энергетических, материальных) между работами: из зон менее напряженных в зоны, объединяющие наиболее напряженные работы; 2. Сокращение трудоемкости части работ критического пути за счет передачи на другие пути, имеющие резервы времени; 3. Параллельное выполнение критических работ; 4. Пересмотр (изменение) топологии сетей, состава работ и структуры сети. Во всех задачах оптимизации может использоваться компьютерное моделирование (имитационное моделирование). Оптимальный сетевой график находится многократными расчетами при различных параметрах сети.
Оптимизация сетевого графика по схеме «Время- Стоимость» Для оптимизации сетевого графика используется частная оптимизация (уменьшение стоимости проекта). При использовании метода «время - стоимость» предполагают, что уменьшение продолжительности работ пропорционально возрастанию ее стоимости. Каждая работа (i,j) характеризуется продолжительностью t(i,j), которая может находиться в пределах
a(i,j) - минимальная возможная продолжительность работы (i,j); b(i,j) - максимальная продолжительность этой работы; t(i,j) - наиболее вероятная продолжительность работы (i,j). При этом стоимость C(i,j) работы (i,j) заключена в границах: Сmax - минимальная стоимость работы, оптимистическая оценка стоимости работы, стоимость при минимальных сроках выполнения работы; Cmin - максимальная стоимость работы, пессимистическая оценка стоимости работы, стоимость при максимальных сроках выполнения работы. Далее при оптимизации вычисляют: h(i,j) - коэффициент увеличения затрат от ускорения работы (i,j);
C(i,j) - наиболее вероятная стоимость проекта
Таким образом, увеличение продолжительности работ может привести к уменьшению стоимости проекта, но продолжительность каждой работы целесообразно увеличить на такую величину, чтобы не изменить ранние сроки наступления всех событий сети. Это означает с одной стороны - продолжительность каждой работы можно увеличить на свободный резерв времени, с другой - эта продолжительность не должна превышать предельно допустимую продолжительность b(i,j). Оптимальную продолжительность работы можно найти на основе соотношения:
где В этом случае стоимость выполнения работы находят по формуле:
Оптимизированный проект имеет суммарную стоимость:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (i)=
(i)= 
 (j) =
(j) =  ,
, – полный путь, предшествующий j-ому событию
– полный путь, предшествующий j-ому событию (i) =
(i) = 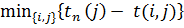
 - множество последующих событий
- множество последующих событий (i) -
(i) -  (i,j) =
(i,j) = 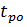 (i,j) =
(i,j) =  (i,j) =
(i,j) = 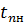 (i,j) =
(i,j) =  (i,j) =
(i,j) =  (i,j) показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится.
(i,j) показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. (i,j) =
(i,j) =  (i, j) =
(i, j) =  (i, j) представляет часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события.
(i, j) представляет часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. (i, j) =
(i, j) =  (i, j) =
(i, j) =  – t (L)
– t (L)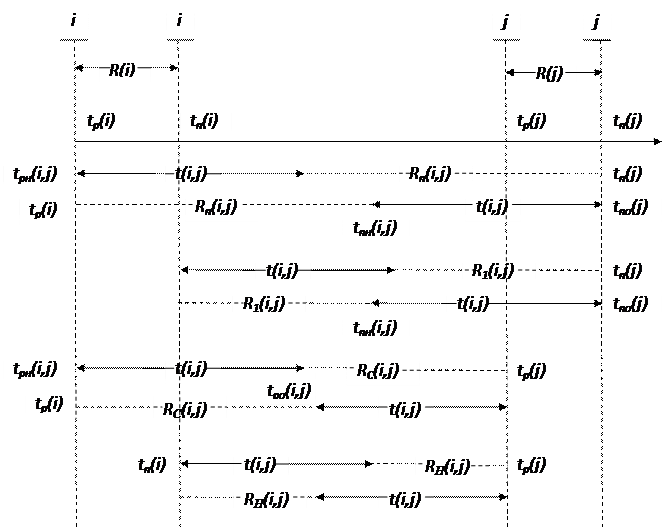
 , где
, где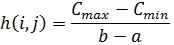

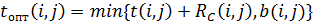 или
или
 ; .
; .