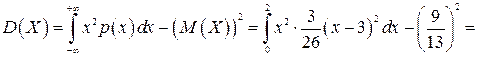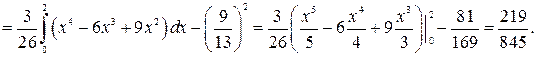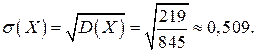|
|
Непрерывные случайные величины.Случайная величина Хназывается непрерывной,если ее функция распределения F(x) при всех значениях х непрерывна и, кроме того, имеет производную Менее строго определение непрерывной СВ можно сформулировать следующим образом: если множество значений случайной величины X заполняет (непрерывно) конечный или бесконечный промежуток на числовой оси, то такая случайная величина называется непрерывной. Если Х– непрерывная случайная величина, то вероятность того, что она примет одно определенное значение равна нулю:
поэтому выполняются равенства:
Плотностью распределения вероятности случайной величины Хв точке х называется предел отношения вероятности попадания значений этой величины в интервал (х, х+∆х) к длине ∆х отрезка [х, х+∆х], когда последняя стремится к нулю:
Интеграл от функции p(x) по промежутку (-∞; х) равен значению функции распределения F(x) для верхнего предела интегрирования, т.е.
Вероятность попадания значений случайной величины Х в интервал (α;β) равна определенному интегралу от плотности распределения p(x) по отрезку [α;β]:
Свойства плотности распределения: 1. Плотность распределения р(х)– неотрицательная функция: p(x)≥0. 2. В точках дифференцируемости функции распределения F(x) ее производная равна плотности распределения: 3. Интеграл по бесконечному промежутку (-∞;+∞) от плотности распределения равен единице: Если все возможные значения случайной величины Х принадлежат отрезку [α;β], то График функции y=p(x) называют кривой плотности распределения вероятностей случайной величины Х (кривой вероятностей, кривой распределения). Математическое ожидание непрерывной случайной величины Х определяется формулой: Дисперсиянепрерывной случайной величины Х определяется по формулам:
---------------------------------------------------------------------------------------------------------------- Непрерывные случайные величины. Стр.1 Пример 1. Случайная величина X задана функцией распределения
Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (–1; 1). Решение. Вероятность того, что X примет значение, заключенное в интервале (a; b), равна приращению функции распределения на этом интервале:
Найти коэффициент a. Решение. Коэффициент a определяем с помощью равенства Поэтому
Пример 3. Плотность вероятностей случайной величины Х задана формулой
Найти ее числовые характеристики: математическое ожидание, дисперсию, среднеквадратическое отклонение. Решение. Найдем математическое ожидание:
Вычислим дисперсию:
Отсюда найдем среднеквадратическое отклонение: ---------------------------------------------------------------------------------------------------------------- Непрерывные случайные величины. Стр.2 Задачи для самостоятельного решения. №1. Случайная величина Х задана функцией распределения: Найдите плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины Х. №2. Случайная величина Х имеет плотность вероятностей:
Найдите: а) постоянную c; б) функцию распределения F(x); в) вероятность события №3. Закон распределения непрерывной случайной величины задан функцией плотности распределения вероятности. Требуется: а) определить значение параметра с; б) построить график функции плотности распределения; в) найти функцию распределения данной случайной величины и построить ее график; г) вычислить среднее квадратичное отклонение.
Домашнее задание к практической работе №7. №1. Закон распределения непрерывной случайной величины задан функцией плотности распределения вероятности.
Требуется: а) определить значение параметра с; б) построить график функции плотности распределения; в) найти функцию распределения данной случайной величины и построить ее график; г) вычислить среднее квадратичное отклонение. №2. Случайная величина Х задана функцией распределения:
Найдите плотность распределения вероятностей, математическое ожидание, дисперсию случайной величины Х и вероятность попадания СВ Х на отрезок [1,5;1,9]. Построить графики функций p(x) и F(x). ---------------------------------------------------------------------------------------------------------------- Непрерывные случайные величины. Стр.3 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
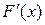 всюду, за исключением, может быть, отдельных точек.
всюду, за исключением, может быть, отдельных точек.


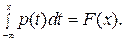



 т.к. p(x)=0 вне этого отрезка.
т.к. p(x)=0 вне этого отрезка.
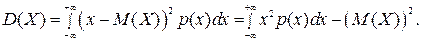

 Положив a=–1, b=1, получим:
Положив a=–1, b=1, получим: Пример 2. Пусть плотность вероятностей р(x) случайной величины X равна
Пример 2. Пусть плотность вероятностей р(x) случайной величины X равна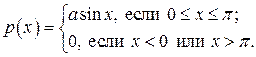

 отсюда
отсюда Следовательно, а=1/2.
Следовательно, а=1/2.