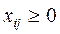|
|
Примеры выполнения заданийЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ ПРАКТИЧЕСКОЕ ПОСОБИЕ
Для студентов 3 курса экономического факультета Гомель 2006 Содержание Введение Содержание дисциплины 1. Теоретические основы метода моделирования 2. Методы решения задач оптимального планирования деятельности предприятия Тема 1 Графический метод решения задач оптимального планирования Тема 2 Решение задач оптимального планирования симплекс-методом 3. Модели исследования операций Тема 1 Игровые методы и модели их использования Тема 2 Сетевые модели Примеры выполнения заданий Задания: 1.Полосы листового проката длиной 200 см необходимо разрезать на заготовки трех типов: А, Б и В длиной соответственно 57, 82 и 101 см для производства 50 изделий. На каждое изделие нужно по 4 заготовки типов А и Б и 5 заготовок типа В. Определить, какое количество полос проката необходимо разрезать тем или иным способом для получения требуемого количества изделий, чтобы отходы от раскроя были наименьшими.
Решение. Рассмотрим возможные способы раскроя одной ‚полосы на заготовки заданных типов. Для составления целевой функции, выражающей суммарную величину отходов, подсчитаем величины отходов при раскрое одной полосы по каждому из способов. При первом способе отходы от каждой полосы составят 200 — 57 х 3 = 29 (см), при втором способе 200 - (57 х 2 + 82) = 4 (см) и т.д. Полученные результаты сведем в таблицу 2.
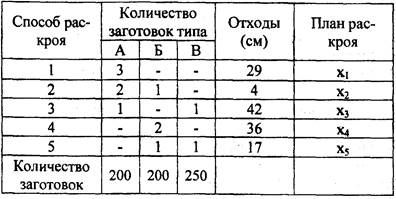
Таблица 2 — Способы раскроя
Для производства 50 изделий необходимо 4 х 50 = 200 заготовок типа А, 4 х 50 = 200 заготовок типа Б и 5 х 50 = 250 заготовок типа В. Введем следующие обозначения: j — индекс способа раскроя; i — индекс типа заготовки; хj — количество полос, раскраиваемых j-м способом,
aij — количество заготовок i-го типа, получаемое при j-м способе раскроя, Сj — отходы при раскрое одной полосы j-м способом раскроя; Bi — требуемое количество заготовок i-го типа. В принятых обозначениях целевая функция задачи, выражающая минимум суммарной величины отходов при всех способах раскроя, будет иметь вид:
Ограничения задачи, показывающие общее количество заготовок каждого типа, которое необходимо получить при раскрое, будут иметь вид:
Обязательным является ограничение на неотрицательное значение количества раскраиваемых каждым способом исходных полос листового проката:
Если раскрыть знаки сумм и проставить значения индексов, то математическая модель задачи будет иметь вид: Z = С1х1+С2х2+С3х3+С4х4+ С5х5 при ограничениях а11 х1 + а12 х2 + а13 х3 + а14 х + а15 x5 = В1, а21 х1 + а22 х2 + а23 х3 + а24 х4 + а25 x5 = В2, а31 х1 + а32 х2 + а33 х3 + а34 х4 + а35 x5 = В3, х1 >= 0, х2 >= 0, х3 >= 0, х4 >= 0, х5 >= 0. Подставив численные значения используемых величин, получим следующую математическую модель задачи: Z=29x1,+4x2+42x3+36х4+ 17х5 à min при ограничениях: 3х1 + 2х2 + х3 = 200, x2+ 2х4 + х5 = 200, х3 + х5 = 250, х1 >= 0, х2 > =0, х3 >= 0, x4 >= 0, х5 >= 0. Решив задачу симплекс-методом, получим следующее оптимальное решение: х1 =0, х2 = 50, х3 = 100, х4 = 0, x5 = 150, Z = 6950 (ем). То же значение целевой функции получается и при другом плане раскроя: х1 = 50, х2 = 0, х3 = 50, х.4 = 0, x5 =200.
2. Составить оптимальный суточный рацион кормления на стойловый период для дойных коров живой массой 500 кг и суточным удоем 32 кг. На одну голову в сутки требуется не менее 22 кг кормовых единиц и 2502 г перевариваемого протеина. Рацион составляется из трех видов кормов: комбикорма, сена и силоса. Содержание питательных веществ в единице каждого вида корма и себестоимость кормов показаны в таблице 3. Согласно физиологическим особенностям животных в рационе должно содержаться не менее 30% концентратов и не более 25% грубых кормов от общей потребности в кормовых единицах. Критерием оптимальности считается минимум себестоимости рациона.
Таблица 3 — Исходные данные
Решение.
Введем следующие обозначения: i — индекс вида корма; j — индекс вида питательного вещества; хi — искомое содержание i-го корма в рационе; Сi — себестоимость 1 кг i-го корма; aij — содержание j-го питательного вещества в кг i-го корма; Вj — количество j-го питательного вещества, необходимое для нормального развития животного; di, — необходимое количество i-го корма в рационе. В принятых обозначениях математическая модель задачи имеет вид:
при ограничениях
i = 1 xi >=di , i = 1, xi <=di , i = 2, xi >=0 , i = 2,3
Если раскрыть знаки сумм и проставить значения индексов, то математическая модель задачи будет иметь вид: Min Z = С1 х1+ С2 х2 + С3 х3 при ограничениях a11 x1 + а12 х2 + а13 х3 >= В1, а21 х1 + а22 х2 + а23 х3 >= В2, x1 >=d1, x2 <=d2 , x2>=0, x3>=0.
В численном виде математическая модель задачи имеет вид
min Z = 14х1 + 3х2 + 2х3 при ограничениях на содержание питательных веществ в рационе
х1 + 0.5х2+ 0.2х3 >= 22, 0.16х1 + 0,06х2 + 0,03х3 >= 2,502, а также условиях по содержанию концентратов (не менее, чем 22 х 0,3 = 6,6 кг), и грубых кормов (не более, чем 22 х 0,25 = 5,5 кг) в рационе x1>= 6,6; x2 <= 5,5; x2 >= 0 x3 >= 0.
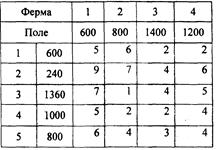
3. В хозяйстве за время уборки при заготовке силоса необходимо перевезти 4000 т зеленой массы с пяти полей к четырем фермам. Имеющееся количество зеленой массы на каждом поле, потребность в зеленой массе каждой фермы, а также стоимость перевозки зеленой массы между полями и фермами приведены в таблице 4. Требуется составить такой план перевозки зеленой массы, при котором общая стоимость перевозки была бы минимальной.
Таблица 4 — Исходные данные
Решение. Введем следующие обозначения: Хij - количество зеленой массы, переводимое с i-го поля к j–й ферме; Сij — стоимость перевозки зеленой массы с i-го поля к j–й ферме; Аi - количество зеленой массы на i-м поле; Вj - потребность в зеленой массе j-й фермы.
В общем виде математическая модель задачи имеет следующий вид:
при ограничениях:
Развервугьтй вид модели: minZ = С11 x11 + С12 x12 + С13 х13 + С14 х14 + С21 х21 + С22 х22 + C23 x2З + С24 x24 + С31 х31 + С32 х32 + С33 х33 + С34 х34 + С41 х41 + C42 x42 + С43x43 + С44 x44 + С51 х51 + С52 х52 + С53 х53 + С54 х54 при ограничениях: x11+ x21 + x31 + x41+ x51 = В1, x12 + x22 + x32 + x42 + x52 = В2, x13+ x23 + x33 + x43 + x53 = В3, x14 + x24 + x34 + x44 + x54 = В4, x11 + x12 + x13 + х14 = а1, x21+ x22 + x2З + x24 = а2, x31+ x32 + x33+ х34 = а3, x41 + x42 + x43 + х44 = а4, x51+ х52 + x53 + x54 = а5, xij >= 0. Математическая модель в численном виде записывается следующим образом: найти minZ= 5х11 + 6х12 + 2х13 + 2х14 + 9х21 + 7х22 + 4x21 + 6х24 + 7х31 + х32 + 4х33 + 5х34 + 5х41 + 2х42 + 2х43 + 4x44 + 6x51 + 4х52 + 3х53 + 4х54 при ограничениях: x11 +x21 +x31 +х41 +x51 = 600, x12 + x22 + x32 + х42 + x52 = 800, x13+ x23 + x33 + x43 + x53 = 1400, x14 + x24 + x34 + x44 + х54 = 1200, x11 + x12 + x13 + x14 = 600, x21 + x22 + x23 + x24 = 240, x31 + x32 + x33 + x34 = 1360, х41 + х42 + x43 + x44 = 1000, x51+ х52 + x53 + x54 = 800.
В результате решения задачи получаем следующий план перевозок: х31 = 560, х41 = 40, х32 = 800, х23 = 240, х13 = 960, х53 = =200, x14 = 600, х54=600, Z= 12000.
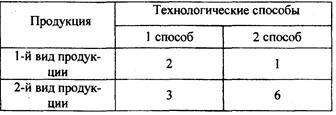
Задания: 1Для выпуска продукции определенного вида используется два способа. Известны общее количество ресурсов В и А и их затраты на единицу продукции при каждом способе (таблица 5).
Таблица 5 — Исходные данные
Максимизировать выпуск продукции при данном объеме ресурсов.
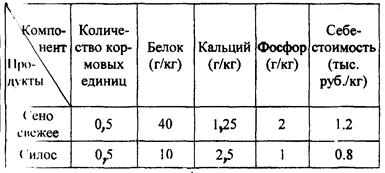
2 При составлении суточного рациона кормления скота можно использовать свежее сено (не более 50 кг) и силос (не более 85 кг). Рацион должен обладать определенной питательностью (число кормовых единиц не менее 30) и содержать питательные вещества: белок (не менее 1 кг), кальций (не менее 100 г) и фосфор (не менее 80 г). В таблице 6 приведены данные о содержании указанных компонентов в 1 кг каждого продукта питания и себестоимости (тыс. руб./кг) этих продуктов. Определить оптимальный рацион из условия минимума себестоимости.
Таблица — 6 Исходные данные
3 Из листов размером 4 х 12 м выкроить заготовки прямоугольной формы размерами 3 х 3 и 2 х 3 метра и составить 90 комплектов, в каждый из которых входит 2 детали первого вида и 10 деталей второго. Определить, сколько листов и по какому варианту раскроить, чтобы использовать при этом минимальное количество листов.
4 Определить минимальное количество сырья, необходимого для производства двух видов продукции в объеме 85 единиц первого вида и 150 единиц второго вида при использовании двух технологических способов. Нормы получения продукции из единицы сырья при каждом технологическом способе приведены в таблице 7.
Таблица 7 — Исходные данные
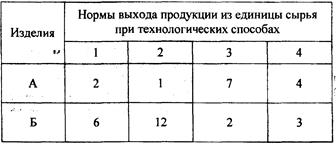
5 Определить минимальное количество сырья, необходимое для изготовления 26 изделий А и 96 изделий Б, используя четы ре технологические способа. Нормы выхода продукции из единицы сырья заданы в таблице 8.
Таблица 8 — Исходные данные
6 В сплаве должно содержаться не менее 8 единиц химического элемента А, 21 единиц — элемента Б и 16 единиц — элемента В. Предприятие закупает металлический лом двух видов: 1 и 2. В таблице 9 указано содержание химических элементов в ломе каждого вида и цена единицы лома. Минимизировать расходы при закупке необходимого предприятию металлического лома. Таблица 9 — Исходные данные
7 Для производства столов и стульев имеются ресурсы трех видов: доски 1-го типа — 500 м, доски 2-го типа — 290 м и трудовые ресурсы 440 чел.-ч. От реализации столов организация получает прибыль в размере 12 у.д.е., стульев - 5 у.д.е. Затраты ресурсов на единицу изделия представлены в таблице 10. Таблица 10 - Исходные данные
Определить выпуск продукции при максимальной прибыли.
8В два пункта А и В прибыло 30 вагонов с некоторым грузом, по 15 вагонов в каждый пункт. Все вагоны требуется доставить в пункты потребления С и Д, причем в пункт С необходимо доставить 10 вагонов, а в пункт Д — 20. Известно, что транспортировка одного вагона из пункта А в пункты С и Д стоит соответственно 1 и 3 денежные единицы, и из пункта В соответственно 2 и 5 единиц. Определить план перевозок, минимальный по стоимости.
9 Для изготовления двух видов продукции используется три вида сырья, нормы расхода сырья на единицу каждого вида продукции и стоимость единицы продукции указаны в таблице 11.
Таблица 11 Исходные данные
Максимизировать выпуск продукции.
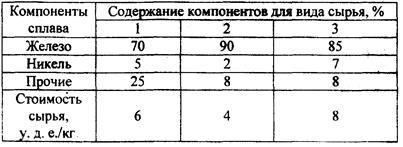
10 В сплав может входить не менее 4 % никеля и не более 80 % железа. Для составления сплава используется три вида сырья, содержащего никель, железо и прочие вещества. Стоимость различных видов сырья и процентов содержания в нем соответствующих компонентов сплава представлены в таблице 12.
Таблица 12 — Исходные данные
Определить состав сырья, минимизирующий стоимость сплава.
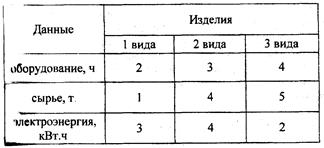
11Цех выпускает три вида изделия. Производственные возможности цеха характеризуются данными в) суточный фонд рабочего времени оборудования — 780 ч; б) суточный расход сырья — 850 т; в) суточный расход электроэнергии — 790 кВт. Ч; Нормы затрат ресурсов на единицу продукции представлены в Таблице 13.
Таблица 13 — Исходные данные
Оптовая цена изделия 1 — 8 у.д.е., изделия 2 - 7 у.д.е., изделия 3 —6 у.д.е.. Максимизировать объем выпуска продукции.
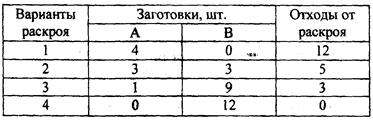
12 Из листового проката определенной формы необходимо нарезать некоторое количество заготовок двух типов А и В для производства 90 штук изделий. Для одного изделия требуется 2 заготовки типа А и 10 заготовок типа В. Возможны четыре варианта раскроя одного листа проката. Количества заготовок А и В, вырезаемых из одного листа при каждом варианте раскроя, и отходы от раскроя указаны в таблице 14.
Таблица 14 — Исходные данные
Какое количество листов проката нужно раскроить каждым вариантом для изготовления 90 штук изделия, чтобы отходы от раскроя были минимальными.
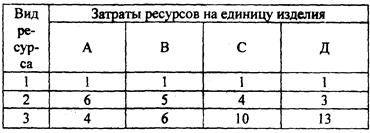
13 Для изготовления изделий А, В, С и Д имеется 16 единиц ресурса первого вида, 1 10 единиц ресурса второго вида и 104 единицы ресурса третьего вида. Стоимость единицы изделия А 60 у.д.е., изделия В — 70 у.д.е., изделия С — 120 у.д.е. и изделия Д — 130 у.д.е. Определить максимальный выпуск продукции, если затраты ресурсов на единицу каждого ее вида следующие (таблица 15). Таблица 15 — Исходные данные
14 Составить наиболее дешевый рацион из трех веществ. В состав рациона должно входить не менее 12 единиц вещества А, не менее 21 единицы вещества В и не менее 32 единиц вещества С. Имеется три вида продуктов (1,2 и 3), содержащих эти вещества в количествах, приведенных в таблице 16. Стоимость одной единицы продукта 1 составляет 20 у.д.е., продукта 2 — 20 у.д.е., продукта 3 — 10 у.д.е.
Таблица 16 — Исходные данные
15 Для производства четырех видов продукции затрачивается три вида ресурсов А, В и С. Затраты ресурсов на единицу продукции заданы в таблице. Известно, что от реализации первого вида продукции предприятие получает прибыль 3 у.д.е., второго - 4 у.д.е., третьего — 3 у.д.е. и четвертого — 1 у.д.е. Определить, какие виды продукции предприятие должно производить и в каком объеме, чтобы получить максимум дохода, если предприятие имеет ресурса А — 12 единиц, В — 8 единиц, С — 48 единиц (таблица 17).
Таблица 17 — Исходные данные
16 В смесь должно входить не менее 12 единиц вещества А, 21 единицы вещества В и 32 единицы вещества С. Вещества содержатся в трех продуктах в следующих пропорциях: в первом продукте вещества А — 1 единица, вещества В — З единицы и вещества С — 4 единицы, во втором продукте соответственно 1 — 2 — З и в третьем продукте 2 — 1 — 2. В каком количестве должны входить продукты в смесь, чтобы стоимость ее была минимальной, если учесть, что весовая единица первого продукта стоит 20 у.д.е., второго — 20 у.д.е., третьего — 10 у.д.е.
17 Необходимо из имеющегося сырья выпустить не менее 20 изделий А, 8 изделий Б, 60 изделий В. Известно, что из 2 единиц сырья первого вида и 1 единицы сырья второго вида получается одно изделие А , из 2 единиц сырья первого вида и 4 единиц второго вида — изделие Б, из 10 единиц сырья первого вида, 4 - второго и 2 единиц третьего получается одно изделие В. Единица сырья первого вида стоит 5 у.д.е., второго — 4 и третьего — 2 у.д.е. Определить затраты сырья каждого вида на производство всех изделий, минимизируя его общую стоимость.
18 Из листов материала размером 6 х 13 метров необходимо получить заготовки двух типов: типа А размером 4 х 5 метра - 800 штук и типа В размером 2 х 3 метра в количестве 400 штук. Составить план раскроя, при котором суммарные отходы были бы минимальными.
19 На предприятии имеется 400 тыс. литров алкилата, 250 тыс. литров крекинг-бензина, 350 тыс. литров бензина прямой перегонки и 100 тыс. литров изопентона. В результате смешивания этих четырех компонентов в разных пропорциях образуется три сорта авиационного бензина: А — 2:3:5:2, бензина Б — 4:1:2:1 и бензина С — 2:2:1:3. Стоимость 1 тыс. литров бензина А равна 110 у.д.е., бензина Б — 100 у.д.е., бензина С — 150 у.д.е. Определить план смешивания компонентов, при котором будет достигнута максимальная стоимость всей продукции.
20 Имеется четыре вида сырья: первого — 24 единицы, второго — 80, третьего — 10 и четвертого 6. Из этого сырья производится три вида продукции: А, В и С. Определить, сколько продукции каждого вида необходимо производить из имеющегося сырья для получения максимального дохода, если прибыль от реализации продукции А составляет 18 рублей, В — 12 у.д.е. и С 8 у.д.е. Нормы затрат сырья на единицу продукции следующие таблица 18).
Таблица 18— Исходные данные
21 Составить наиболее дешевую смесь из трех веществ. В состав должно входить не менее 6 единиц химического вещества А, не менее 8 единиц вещества В и не менее 12 вещества С. Имеется три вида продуктов (1, 2, 3), содержащих эти химические вещества в следующих количествах (таблица 19).
Таблица 19 — Исходные данные
Стоимость одной весовой единицы продукта 1 — 2 у.д.е., продукта 2 — 3 у.д.е., продукта 3 2,5 у. д.е.
22 На рынок в город привозят одним видом транспорта картофель 12 у.д.е, 11 у.д.е и 9 у.д.е. за килограмм из 1, 2 и 3 совхозов соответственно. На погрузку тонны картофеля ленточным методом требуется: в первой совхозе — 1 мин, во втором — 4 мин, в третьем —3 мин. Для своевременного поступления продукции на рынок необходимо, чтобы на погрузку 12 т., требуемых населению города на каждый день, затрачивалось не более 40 мин. Сколько надо привозить картофеля из этих совхозов, чтобы общая стоимость картофеля на рынке была минимальной, если известно, что 1 совхоз может ежедневно отправлять не более 10 т, 2 совхоз — не более 8 т, 3 совхоз — не более 6т?
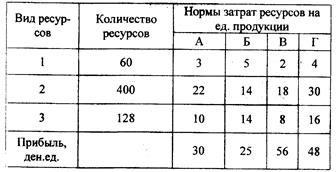
23 Для изготовления изделий А, Б, В, Г используется три вида ресурсов. Затраты ресурсов на единицу продукции и прибыль от реализации единицы продукции приведены в таблице. Определить, сколько и какой продукции надо выпустить, чтобы получить максимальную прибыль (таблица 20).
Таблица 20 — Исходные данные
24 На двух станках разного типа необходимо изготовить пять видов изделий. Известны затраты времени на изготовление одного изделия на каждом станке и стоимость обработки единицы изделия (таблица 21).
Таблица 21 — Исходные данные
Сколько изделий каждого типа будет изготовлено, если фонд времени 1 – го станка 200 часов, 2-го— 300 часов. Фонд времени должен быть использован полностью, при этом необходимо добиться минимальной стоимости обработки.
25Составить план производства четырех деталей на участке, располагающем тремя группами оборудования. Добиться при этом минимальной стоимости изготовления деталей. Исходные данные в таблице 22. Запланированный объем производства деталей — 5300 у.д.е. Оборудование должно быть загружено полностью.
Таблица 22 - Исходные данные
26 Груз, находящийся в пунктах А и В, необходимо перебазировать в пункты С и Д. В пунктах А и В имеются грузы соответственно на 6 и 4 машины. В пункты С и Д надо отправить соответственно 3 и 7 машин груза. Расстояния между пунктами в км. заданы следующей матрицей (таблица 23).
Таблица 23 — Исходные данные
Требуется спланировать перевозки так, чтобы суммарный пробег машин был наименьшим.
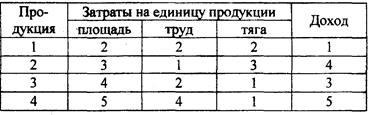
27 Хозяйство располагает следующими ресурсами: площадь - 100 ед., труд — 120 ед., тяга — 80 ед. Хозяйство производит четыре вида продукции: 1, 2, 3, 4. Затраты на производство единицы каждого вида продукции и доход от их производства указаны в таблице 24.
Таблица 24 — Исходные данные
Определить план производства продукции, дающий максимальную сумму дохода.
28 Из листового материала размером 5 х 12 м необходимо получить заготовки трех типов: типа А размером 4 х 8 м в количестве 500 штук, типа В размером 1 х 4 м в количестве 1000 штук и типа С размером 2 х 6 м в количестве 100 штук. Составить план раскроя, минимизирующий расход исходного материала.
29 Трикотажная фабрика использует для производства свитеров и кофточек чистую шерсть, силон и нитрон, запасы которых соответственно 900, 400 и 300 кг. Количество Пряжи каждого вида в кг, необходимой для изготовления 10 изделий, а также прибыль, получаемая от их реализации, приведены в таблице 25.
Таблица 25 — Исходные данные
Определить план выпуска изделий, максимизирующий прибыль.
30 Из листов стали размером 5 х 10 м выкроить детали двух видов, одну размером 3 х 6 м, другую размером 2 х 4 м, Из выкроенных деталей составить 60 комплектов, в каждый из которых входит 2 детали первого вида и З второго. Определить, сколько листов и по какому варианту нужно раскроить, чтобы минимизировать отходы.
31 Из листов стали размером 6 х 13 м выкроить детали двух видов, одну размером 4 х 5 м, другую размером 2 х 3 м. Деталей первого вида необходимо получить 800 штук, а деталей второго 400 штук. Определить, сколько листов и по какому варианту нужно раскроить, чтобы минимизировать отходы, предварительно составив варианты раскроя целых листов на детали.
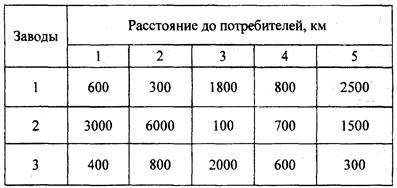
32Планом определено строительство трех машиностроительных заводов с годовым выпуском продукции соответственно в 500, 800 и 850 млн. руб. Их продукция будет потребляться в 5 экономических районах, причем потребности первого района определены в 400 млн. руб., второго — 200, третьего — 300, четвертого — 200 и пятого — 650. Матрица расстояний между поставщиками и потребителями задана в таблице 26.
Таблица 26 — Исходные данные
Составить план закрепления экономических районов за поставщиками, который минимизировал бы суммарные грузоперевозки. 33 Распределить работу между тремя рабочими таким образом, чтобы максимизировать выпуск деталей трех видов. Трудоемкость изготовления деталей рабочими, их цена, а также фонд времени каждого рабочего приведены в таблице 27.
Таблица 27 — Исходные данные
34 Из пруткового проката длиной 2 м необходимо нарезать некоторое количество заготовок А и Б длиной соответственно 150 и 620 мм для производства 100 изделий. Для одного изделия требуется по 2 заготовки каждого типа. Возможны следующие варианты раскроя (таблица 28).
Таблица 28 — Исходные данные
Минимизировать общий расход материала при раскрое.
35 В мастерской освоено производство столов и тумбочек для торговой сети. Имеется два вида древесины — 72 м3 и 56 м3. На каждое изделие требуется определенное количество древесины каждого вида, приведенное в таблице 29.
Таблица 29 — Исходные данные
Кроме того, от производства одного стола может быть получен чистый доход в 1,1 ден. единиц, а от одной тумбочки 0,7 ден. единиц. Определить, сколько столов и тумбочек должна производить мастерская для получения максимального дохода.
2 Методы решения задач оптимального планирования деятельности предприятия Тема 1 Графический метод решения задач оптимального планирования Графический метод используется для решения задач линейного программирования с двумя переменными, заданными в симметричной форме, и многими переменными, заданными в канонической форме (при условии, что они содержат не более двух свободных переменных). Решение задачи графическим способом проводится в последовательности: а) записывают уравнения граничных прямых и строят плоскости Х1 0 Х2; б) определяют полуплоскости, соответствующие исходным ограничениям-неравенствам. Для этого берут произвольную точку, лежащую по ту или иную сторону от граничной прямой и ее координаты подставляют в левую часть ограничения-неравенства. Если оно удовлетворяется, то искомой будет полуплоскость, которая содержит выбранную точку; если не удовлетворяется, то искомой будет полуплоскость, которой данная точка не принадлежит; в) выделяют область допустимых решений задачи как общую часть m+2 полуплоскостей, где m полуплоскостей соответствует исходным неравенствам задачи, а две полуплоскости - условию неотрицательности искомых переменных; г) строят вектор V = (С1; С2)и перпендикулярно к нему одну из прямых семейства Z, например Z=0; д) определяют экстремальную точку многоугольника решений путем параллельного перемещения вспомогательной прямой Z=0 в направлении вектора V; е) вычисляют координаты оптимальной точки и значение функции Z . Задачу со многими переменными можно решить графически, если в ее канонической записи присутствует не более двух свободных переменных. Чтобы решить такую задачу в системе ограничительных уравнений необходимо выделить базисные переменные, а затем их следует опустить и перейти к эквивалентной системе неравенств. Целевая функция также должна быть выражена только через свободные переменные. Полученную двумерную задачу решают обычным графическим методом. Найдя две координаты оптимального решения, подставляют их в уравнения ограничений исходной задачи и определяют остальные координаты оптимального решения. Решая графически получившуюся двумерную задачу необходимо помнить, что на каждой граничной прямой соответствующее неравенство обращается в равенство, поэтому опущенная при образовании этого неравенства базисная переменная равна нулю, В связи с этим в каждой из вершин области допустимых решений по крайней мере две переменные исходной задачи принимают нулевые значения.
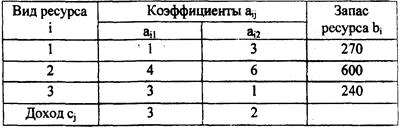
Примеры выполнения заданий Задания: 1 Построить модель производственной задачи, использующей две технологии и три вида ресурсов при значениях величин aij, bi, и bj,. заданных таблицей 30.
Таблица 30 — Исходные данные
Решить задачу графически.
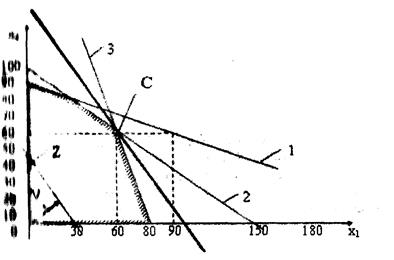
Решение. Математическая модель задачи в численном виде может быть записана следующим образом: mах Z: 3х1 + 2х2, при ограничениях х1 + 3х2 <= 270, 4x1 + 6х2 <= 600, 3x1 + х2 <= 240, x1 >= 0, x2 >= 0. Для построения допустимой области решений, заданной ограничениями - неравенствами, построим на плоскости многоугольник, ограниченный прямыми х1 + 3х2 = 270, 4x1 + 6х2 = 600, 3x1 + х2 = 240 (линии 1, 2 и 3 на рисунке 1) и координатными осями x1 = 0, x2 = 0. Убедимся, что любая точка, лежащая внутри или на границе заштрихованной области, удовлетворяет всем исходным неравенствам системы, подставляя любую из точек заштрихованной области, например, начало координат (0; 0) в каждое из неравенств системы.
Рисунок 1 — Решение
a) х1 + 3х2 = 270, b) 4x1 + 6х2 = 600 c) 3x1 + х2 = 240 x1=90, x2=60, x1=0, x2=100, x1=0, x2=240, x1=0, x2=90, x1=150, x2=0, x1=80, x2=0.
Приравняем правую часть уравнения целевой функции некоторой постоянной величине Z = 90 и построим уравнение прямой 3x1 + 2х2 = 90 (х1 = 0, х2 = 45; х2 = 0, х1 = 30). Увеличивая Z, будем передвигать эту прямую параллельно самой себе в направлении вектора V = (с1;с2)= (3; 2), координатами которого являются коэффициенты при неизвестных уравнения прямой Z. Он перпендикулярен этой прямой и указывает направление возрастания Z. Максимальное значение Z = 300 достигается в точке С с координатами (60; 60), которая является точкой пересечения прямых 4x1 + 6х2 = 600, и 3x1 + х2 = 240.
2 Найти оптимальное сочетание посевов пшеницы и кукурузы на участках различного плодородия площадью 100 и 200 га. Данные приведены в таблице 31.
Таблица 31 — Исходные данные
По плану должно быть собрано не менее 1500 ц. пшеницы и 4500 ц. кукурузы. Цена 1 ц. пшеницы 6 денежных единиц, кукурузы - 4 денежных единицы. Критерием оптимальности считается максимум валовой продукции в денежном выражении.
Решение Если обозначить через х1 — площадь, отводимую под посев пшеницы на 1 участке, через х2 — на 2, через х3 и х4 площади, отводимые под посев кукурузы соответственно на 1 и 2 участках, то ограничения задачи запишутся следующим образом: x1 + х3 = 100, х2 + х4 = 200, 20х1 + 15х2 >= 1500 (ограничение на сбор пшеницы), 35 х3 +30х4 >= 4500 (ограничение на сбор кукурузы), х j>= 0 (j= 1,4). Стоимость пшеницы, которую предполагается собрать с двух участков, составляет 6 (20х1 + 15х2) денежных единиц; стоимость кукурузы - 4 (35 х3 +30х4) денежных единиц, а общая стоимость валовой продукции выразится суммой Z= 120х1 + 90х2 + 140х3 + 120х4, которая должна стремиться к максимуму Для решения задачи графическим способом преобразуем составленную модель в каноническую форму введением дополнительных переменных х5 >= 0 и х6 >= 0: Max Z = 120х1 + 90х2 + 140х3 + 120х4+ 0х5 + 0х6; х1 + х3 = 100, х2 + x4 =200, 20х1 + 15х2 – x5 = 1500 35 х3 +30х4 – x6 = 4500 хj>0 (j= 1,6).
Выделим в системе ограничений какой-либо базис и убедимся, что число свободных переменных не превышает двух. max Z; = 38000 - 20 х1 - 30х2, x3 = 100- х1, = 200 - х2, x5 = -1500+20х1 +15 x2, х6 = 4500-35х1 -30х2. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
; ;
;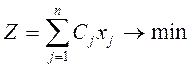
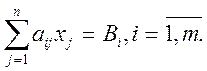
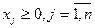
 min
min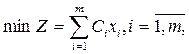

 ,
,  ,
,
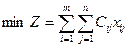 ,
, 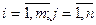

 ,
,
 ,
,