
|
|
Коэффициенты условий работы арматуры12 Коэффициент q
Таблица 2 Коэффициент b
Пример 1. Поверочный расчет железобетонного элемента по первой группе предельных состояний производится по проектным данным. Железобетонный элемент запроектирован по ранее действовавшим нормам (СНиП II-21-75) и выполнен из тяжелого бетона марки М250 и арматуры класса А-III. Определить расчетное сопротивление бетона на сжатие fcd и расчетное сопротивление арматуры на растяжение fyd. Первоначально необходимо перейти от марки М бетона к его условному классу С'. Для этого от средней кубиковой прочности бетона перейдем к гарантированной кубиковой прочности с помощью коэффициента перехода, равного 0,8, и коэффициента, учитывающего различную размерность (кг/см2 и МПа), равного 0,1.
В соответствии с [8]
Для арматуры класса S400 (аналог А-III) нормативное сопротивление равно
Пример 2. На основе методики ускоренной оценки прочности бетона по результатам испытаний определить расчетное сопротивление бетона на сжатие для расчета на прочность fcd. Результаты испытаний бетона:
Среднее значение прочности бетона вычисляется как среднее арифметическое результатов испытаний бетона
Проверяем условие
Пример 3. На основе методики статистической оценки прочности арматуры по результатам испытаний определить расчетное сопротивление арматуры на растяжение fyd. Результаты испытаний арматуры на растяжение:
Вычисляем среднее квадратическое отклонение
нормативное сопротивление арматуры растяжению
и расчетное сопротивление арматуры
Задачи для самостоятельного решения № 1.Железобетонный элемент запроектирован по ранее действовавшим нормам (СНиП II-В.1-62*) и выполнен из тяжелого бетона марки М200. Определить расчетное сопротивление бетона на сжатие fcd для поверочного расчета прочности элемента по проектным данным. № 2.Железобетонный элемент запроектирован по ранее действовавшим нормам. Согласно результатам испытаний 5 образцов среднее значение предела текучести арматуры равно № 3. На основе методики статистической оценки прочности бетона по результатам испытаний определить его расчетное сопротивление на сжатие fcd для расчета по первой группе предельных состояний. Результаты испытаний бетона на сжатие следующие:
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2. Поверочные расчеты прочности железобетонных конструкций эксплуатируемых строительных Цель занятия: научиться выполнять поверочные расчеты прочности эксплуатируемых железобетонных конструкций с учетом их фактического технического состояния, установленного при обследовании. Исходные алгоритмы, рабочие формулы для расчета.В основерешения задач по определению прочности железобетонных элементов лежит применение методик расчета действующих норм с использованием ряда коэффициентов условий работы, учитывающих дефекты и повреждения элементов. При местном разрушении бетона сжатой зоны конструкции поверочный расчет производится при фактических геометрических размерах поперечного сечения за вычетом разрушенного участка (рис. 3, а). При наличии силовых продольных трещин в месте сопряжения полки и ребра изгибаемых элементов таврового поперечного сечения площадь сечения свесов полки в расчете не учитывается (рис. 3, б). При местном снижении прочности бетона сжатой зоны, когда в сжатой зоне расположен бетон разного класса, поверочный расчет (по альтернативной модели) железобетонного элемента производится при приведенном расчетном сопротивлении бетона сжатой зоны (рис. 3, в).
Рис. 3 Коэффициенты условий работы для арматуры железобетонных элементов, учитывающие дефекты и повреждения приведены в табл. 3. Таблица 3 Коэффициенты условий работы арматуры
Пример 4. При обследовании установлено, что в результате воздействия высокой температуры при пожаре прочность бетона сжатой зоны изгибаемого железобетонного элемента различается по высоте (рис. 4). Требуется определить прочность железобетонного элемента, если
Рис. 4
Задаемся высотой сжатой зоны бетона элемента
Вычисляем высоту сжатой зоны элемента
Точность вычисления составляет Принимаем высоту сжатой зоны Тогда
Точность вычисления составляет Относительная высота сжатой зоны бетона и ее граничное значение равны:
где Поскольку условие
Задачи для самостоятельного решения № 4.Изгибаемыйжелезобетонный элемент прямоугольного поперечного сечения (
№ 7. Железобетонная балка покрытия поперечного сечения (рис. 6) из тяжелого бетона условного класса ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3. Поверочные расчеты прочности, трещиностойкости и жесткости железобетонных конструкций по Цель занятия: научиться выполнять поверочные расчеты прочности, трещиностойкости и жесткости эксплуатируемых железобетонных конструкций с учетом их фактического технического состояния, установленного при обследовании, на основе деформационной модели с использованием прикладных программ расчета на ЭВМ. Исходные алгоритмы, рабочие формулы для расчета.В основеопределения параметров напряженно-деформированного состояния эксплуатируемых железобетонных элементов на базе деформационной модели с использованием диаграмм «напряжение-деформация» для бетона и арматуры лежит применение коэффициентов условий работы к расчетному сопротивлению и площади поперечного сечения арматуры, а также учет дефектов и повреждений бетона поперечных сечений элементов. Деформационная модель позволяет производить поверочные расчеты железобетонных элементов произвольной формы поперечного сечения из тяжелых и легких бетонов с различными физико-механическими характеристиками бетона по сечению элемента и произвольным расположением арматуры любых классов, включая предварительно напряженную. В программе «БЕТА», кроме величины внутренних усилий Для изгибаемых железобетонных элементов, работающих как свободно опертые или консольные балки с расчетным пролетом (вылетом)
где Таблица 4 Коэффициент
Окончание табл. 4
Примечание. В случае загружения изгибаемого элемента одновременно по нескольким схемам
Расчет на основе деформационной модели позволяет получить распределение по поперечному сечению относительных деформаций и напряжений на любой стадии работы железобетонного элемента. Варьируя параметрами сечения железобетонного элемента и последовательно производя расчеты с построением графика, можно наглядно продемонстрировать степень влияния дефектов и повреждений на прочность, жесткость и трещиностойкость элемента. Поверочный расчет железобетонного элемента по нормальному сечению на аварийность (установление категории состояния V или IV) для усилий от фактически действующих нагрузок производится по диаграммам деформирования бетона и арматуры при средних значениях их прочностных характеристик.
Пример 5. При обследовании установлено, что в результате воздействия высокой температуры при пожаре условный класс бетона железобетонной балки различается по высоте в соответствии с рис. 4 ( Вычисляем значение максимального изгибающего момента в балке от расчетной и нормативной равномерно распределенных нагрузок:
После ввода исходных данных в соответствии с требованиями программы расчета параметров напряженно-деформированного состояния в нормальном сечении железобетонного элемента «БЕТА», в которой реализована деформационная модель, и выполнения расчета на ЭВМ, получаем следующие результаты: - изгибающий момент, соответствующий прочности железобетонной балки по нормальному сечению - ширина раскрытия трещин, нормальных к продольной оси балки, от действия нормативной нагрузки - по кривизне
Рис. 7
Задачи для самостоятельного решения № 8. Железобетонная балка прямоугольного поперечного сечения ( № 9. Железобетонная колонна расчетной длиной № 10. Свободно опертая железобетонная балка расчетным пролетом № 11. Балка перекрытия из бетона марки М200 (СНиП II-В.1-62*), с арматурой с нормативным сопротивлением
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4. Поверочные расчеты прочности каменных конструкций по результатам их обследования
Цель занятия: научиться по результатам испытаний и проектным данным определять расчетные характеристики материалов эксплуатируемых каменных и армокаменных конструкций, производить их поверочные расчеты прочности с учетом фактического технического состояния, установленного при обследовании.
Рис. 10 Условная марка кирпича, а также раствора по результатам испытаний устанавливается как среднее значение единичных испытаний. В случае испытаний на сжатие пластинок раствора, отобранных из швов кладки, применяется понижающий коэффициент 0,7. Расчетное сопротивление каменной кладки по условным маркам кирпича и раствора, не совпадающим со значениями параметрического ряда [12, табл. 2], вычисляется линейной интерполяцией между ближайшими параметрическими значениями по формуле (2) в соответствии со схемой, изображенной на рис. 11.
где
Рис. 11
В основерешения задач по определению прочности каменных и армокаменных элементов лежит применение методики расчета действующих норм с использованием ряда коэффициентов условий работы к расчетному сопротивлению каменной кладки R, учитывающих дефекты и повреждения эксплуатируемых элементов (см. табл. 5.1). При местном разрушении каменной кладки конструкции поверочный расчет производится при фактических геометрических размерах поперечного сечения за вычетом разрушенного участка. При одностороннем уменьшении поперечного сечения в поверочном расчете следует учитывать фактический эксцентриситет действующих продольных усилий. Поверочный расчет каменных и армокаменных конструкций на аварийность производится для усилий от фактически действующих нагрузок при средних значениях прочностных характеристик каменной кладки и арматуры (для армокаменных конструкций). Пример 6. Центрально сжатый кирпичный столб прямоугольного поперечного сечения с размерами 1030 ´ 510 мм, высотой 6 м из обыкновенного глиняного кирпича пластического прессования в процессе эксплуатации получил повреждения в виде силовых волосных вертикальных трещин, пересекающих менее 4-х рядов кладки. Результаты испытаний на сжатие кирпича и раствора:
Требуется проверить прочность столба при действии кратковременной нагрузки Вычисляем среднее значение прочности кирпича и раствора при сжатии:
проверяем условие
Исключаем из расчета максимальное значение прочности раствора
Таким образом, при сжатии условные марки кирпича и раствора соответственно равны:
Упругая характеристика a для кладки из глиняного кирпича пластического прессования и условной марки раствора М'38 согласно [12, табл. 15] равна Проверяем условие прочности столба при центральном сжатии:
При заданной нагрузке прочность столба не обеспечена – требуется его усиление. Задачи для самостоятельного решения № 12. Центрально нагруженный кирпичный столб прямоугольного поперечного сечения с размерами 770 ´ 770 мм, высотой 4 м из обыкновенного глиняного кирпича пластического прессования в процессе эксплуатации получил повреждения в результате размораживания в виде разрушения наружного слоя кладки по периметру сечения на глубину до половины кирпича. Результаты испытаний на сжатие кирпича и раствора:
Требуется определить прочность столба при действии длительной нагрузки ( № 13. Для исходных данныхпримера 6проверить прочность столба при действии длительной нагрузки № 14. Центрально нагруженный кирпичный столб квадратного поперечного сечения с размерами 510 ´ 510 мм, высотой 3 м из обыкновенного глиняного кирпича пластического прессования условной марки на сжатие М'120 и цементно-песчаного раствора условной марки М'65 имеет сетчатое армирование из круглой стали с расчетным сопротивлением ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5. Поверочные расчеты Цель занятия: научиться по результатам испытаний и проектным данным определять расчетные характеристики металла эксплуатируемых металлических конструкций, производить их поверочные расчеты прочности и жесткости с учетом дефектов и повреждений, установленных при обследовании. Исходные алгоритмы, рабочие формулы для расчета.Расчетное сопротивление металла для поверочных расчетов эксплуатируемых металлических конструкций по прочности определяется с учетом коэффициента надежности

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
, ,
, ,
,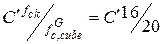 .
.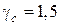 , тогда
, тогда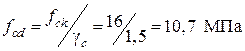 .
. , тогда
, тогда .
.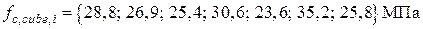 .
.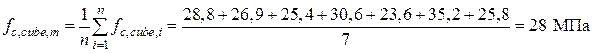 .
.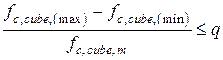 .
. – условие не выполняется. Исключаем из расчета максимальное значение прочности и повторяем расчет.
– условие не выполняется. Исключаем из расчета максимальное значение прочности и повторяем расчет.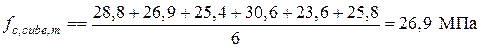

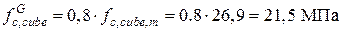
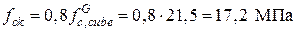
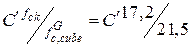
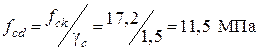 .
.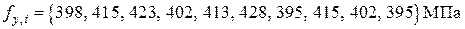 .
. .
.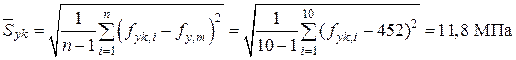 ,
,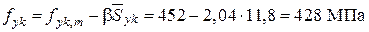 ,
, .
.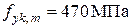 . Определить расчетное сопротивление арматуры на растяжение fyd для поверочного расчета на прочность.
. Определить расчетное сопротивление арматуры на растяжение fyd для поверочного расчета на прочность.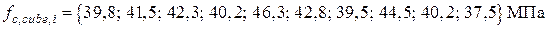 .
.
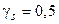
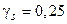
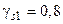
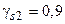
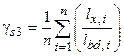
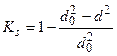
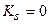
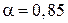 . Размеры сечения элемента:
. Размеры сечения элемента: 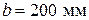 ,
, 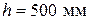 ,
, 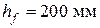 ,
, 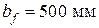 ,
, 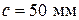 . Элемент имеет арматуру с расчетным сопротивлением
. Элемент имеет арматуру с расчетным сопротивлением 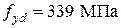 и модулем упругости
и модулем упругости  . Исходная площадь поперечного сечения продольной арматуры составляет
. Исходная площадь поперечного сечения продольной арматуры составляет  (
(  ).
).

 .
.
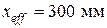 . Определяем приведенное расчетное сопротивление бетона сжатой зоны сечения
. Определяем приведенное расчетное сопротивление бетона сжатой зоны сечения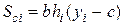 ,
, 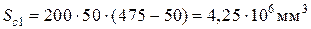 ,
, ,
,  ,
, ,
,  .
. .
. .
.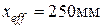 и повторяем расчет. При этом изменится значение толщины слоя, учитываемого в расчете, по которому проходит нижняя граница сжатой зоны:
и повторяем расчет. При этом изменится значение толщины слоя, учитываемого в расчете, по которому проходит нижняя граница сжатой зоны: 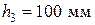 ,
, 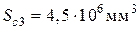 .
.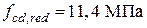 ,
, .
.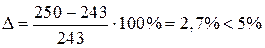 .
.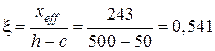 ;
; 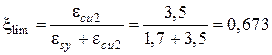 ,
, находим по [8, табл. 6.1],
находим по [8, табл. 6.1], 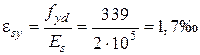 .
.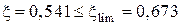 выполняется, продольная арматура достигает в предельной стадии предельных деформаций. Прочность железобетонного элемента по нормальному сечению составляет
выполняется, продольная арматура достигает в предельной стадии предельных деформаций. Прочность железобетонного элемента по нормальному сечению составляет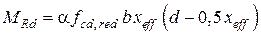 ,
,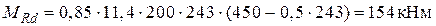 .
. ,
, 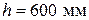 ) из тяжелого бетона с расчетным сопротивлением
) из тяжелого бетона с расчетным сопротивлением 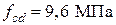 ,
, 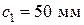 ). Расчетное сопротивление арматуры –
). Расчетное сопротивление арматуры – 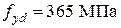 . В процессе эксплуатации элемент получил повреждения в виде продольных трещин вдоль угловых стержней растянутой арматуры в зоне их анкеровки и уменьшение площади поперечного сечения в результате коррозии в зоне действия максимального изгибающего момента
. В процессе эксплуатации элемент получил повреждения в виде продольных трещин вдоль угловых стержней растянутой арматуры в зоне их анкеровки и уменьшение площади поперечного сечения в результате коррозии в зоне действия максимального изгибающего момента  . Требуется определить прочность элемента по нормальному сечению.
. Требуется определить прочность элемента по нормальному сечению. № 5. Железобетонная ребристая плита (рис. 5) с расчетным тавровым поперечным сечением с полкой в сжатой зоне (
№ 5. Железобетонная ребристая плита (рис. 5) с расчетным тавровым поперечным сечением с полкой в сжатой зоне (  ,
,  ,
, 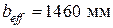 ,
, 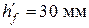 ) выполнена из тяжелого бетона условного класса
) выполнена из тяжелого бетона условного класса 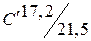 , армирована согласно проектным данным арматурой класса А-III с результатами испытаний на растяжение: среднее значение предела текучести 5 отобранных образцов составляет
, армирована согласно проектным данным арматурой класса А-III с результатами испытаний на растяжение: среднее значение предела текучести 5 отобранных образцов составляет 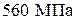 . Нижние стержни поражены коррозией с уменьшением поперечного сечения более 50 %. Требуется определить прочность элемента по нормальному сечению.
. Нижние стержни поражены коррозией с уменьшением поперечного сечения более 50 %. Требуется определить прочность элемента по нормальному сечению.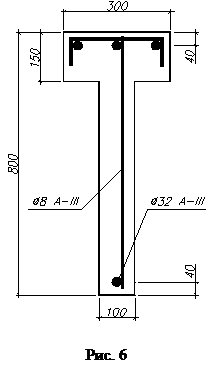 № 6. Железобетонная колонна расчетной длиной
№ 6. Железобетонная колонна расчетной длиной 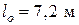 многоэтажного рамного каркаса прямоугольного поперечного сечения (
многоэтажного рамного каркаса прямоугольного поперечного сечения ( 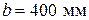 ,
, 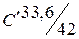 армирована симметрично расположенной в сечении арматурой в сжатой и растянутой зонах по 2Ø18 мм S500 (
армирована симметрично расположенной в сечении арматурой в сжатой и растянутой зонах по 2Ø18 мм S500 ( 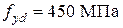 ,
, 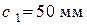 ). В расчетном сечении действует продольная сила
). В расчетном сечении действует продольная сила 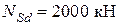 и изгибающий момент
и изгибающий момент  , определенный с учетом случайного эксцентриситета и влияния продольного изгиба. В процессе эксплуатации колонна под воздействием коррозии получила повреждения мест сварки поперечной и наиболее сжатой продольной арматуры. Требуется проверить прочность колонны по нормальному сечению.
, определенный с учетом случайного эксцентриситета и влияния продольного изгиба. В процессе эксплуатации колонна под воздействием коррозии получила повреждения мест сварки поперечной и наиболее сжатой продольной арматуры. Требуется проверить прочность колонны по нормальному сечению. армирована поперечными стержнями Ø8мм А-III (
армирована поперечными стержнями Ø8мм А-III (  ,
,  , приваренными по концам к продольной арматуре Ø32 мм. Временная равномерно распределенная нагрузка –
, приваренными по концам к продольной арматуре Ø32 мм. Временная равномерно распределенная нагрузка – 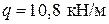 , постоянная с учетом собственного веса балки –
, постоянная с учетом собственного веса балки – 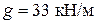 . Поперечная сила у края опоры равна
. Поперечная сила у края опоры равна 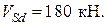 При обследовании балки установлено, что в результате коррозии мест сварки поперечной арматуры с продольной в нижней части ребра нарушена анкеровка поперечной арматуры с одного конца. Требуется проверить прочность балки на действие поперечной силы.
При обследовании балки установлено, что в результате коррозии мест сварки поперечной арматуры с продольной в нижней части ребра нарушена анкеровка поперечной арматуры с одного конца. Требуется проверить прочность балки на действие поперечной силы.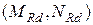 , соответствующих пределу прочности элемента по сечению, нормальному к его продольной оси, вычисляются внутренние усилия
, соответствующих пределу прочности элемента по сечению, нормальному к его продольной оси, вычисляются внутренние усилия 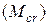 , соответствующие образованию трещин, нормальных к продольной оси элемента, а также ширина их раскрытия
, соответствующие образованию трещин, нормальных к продольной оси элемента, а также ширина их раскрытия 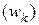 . На любых этапах работы (с трещинами, без трещин, в предельной стадии) при заданных внутренних усилиях
. На любых этапах работы (с трещинами, без трещин, в предельной стадии) при заданных внутренних усилиях 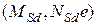 вычисляется кривизна железобетонного элемента.
вычисляется кривизна железобетонного элемента.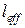 , прогиб определяется по формуле
, прогиб определяется по формуле , (1)
, (1)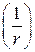 – кривизна элемента в сечении с максимальным изгибающим моментом от нагрузки, при которой определяется прогиб;
– кривизна элемента в сечении с максимальным изгибающим моментом от нагрузки, при которой определяется прогиб; 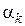 – коэффициент, принимаемый по табл. 4.
– коэффициент, принимаемый по табл. 4. для определения прогибов изгибаемых элементов
для определения прогибов изгибаемых элементов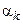
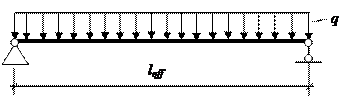
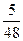
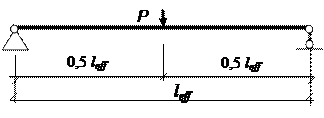
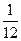





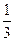
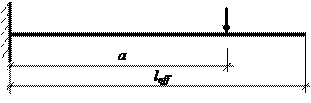

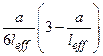
 , а кривизна
, а кривизна  определяется для суммарного изгибающего момента.
определяется для суммарного изгибающего момента. ,
, 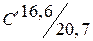 ,
, 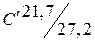 ,
, 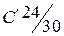 ). Требуется проверить прочность балки при длительном действии расчетной равномерно распределенной нагрузки
). Требуется проверить прочность балки при длительном действии расчетной равномерно распределенной нагрузки 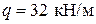 , прогиб и ширину раскрытия трещин, нормальных к продольной оси элемента, в зоне действия максимального изгибающего момента от нормативной нагрузки
, прогиб и ширину раскрытия трещин, нормальных к продольной оси элемента, в зоне действия максимального изгибающего момента от нормативной нагрузки 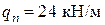 . Класс конструкции по условиям эксплуатации – ХС3 (
. Класс конструкции по условиям эксплуатации – ХС3 ( 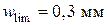 ). Предельно допустимый прогиб балки согласно [13, раздел 10]
). Предельно допустимый прогиб балки согласно [13, раздел 10] 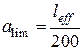 . Размеры сечения элемента:
. Размеры сечения элемента: 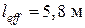 . Элемент армирован стержневой арматурой 2Ø32 мм (исходная площадь поперечного сечения продольной арматуры
. Элемент армирован стержневой арматурой 2Ø32 мм (исходная площадь поперечного сечения продольной арматуры  , установленным по результатам испытаний.
, установленным по результатам испытаний.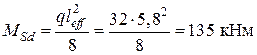 ,
, 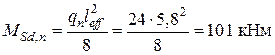 .
.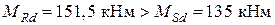 – прочность балки обеспечена, (на рис. 7 для железобетонной балки представлено распределение по сечению относительных деформаций и напряжений в предельной стадии, точка на диаграмме деформирования арматуры демонстрирует достижение стержнем арматуры расчетного сопротивления при растяжении);
– прочность балки обеспечена, (на рис. 7 для железобетонной балки представлено распределение по сечению относительных деформаций и напряжений в предельной стадии, точка на диаграмме деформирования арматуры демонстрирует достижение стержнем арматуры расчетного сопротивления при растяжении); – требуемая трещиностойкость балки обеспечена;
– требуемая трещиностойкость балки обеспечена;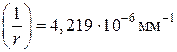 от действия нормативной нагрузки и формуле (1) вычисляем максимальное значение прогиба балки:
от действия нормативной нагрузки и формуле (1) вычисляем максимальное значение прогиба балки: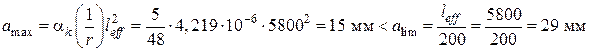 – требуемая жесткость балки обеспечена.
– требуемая жесткость балки обеспечена.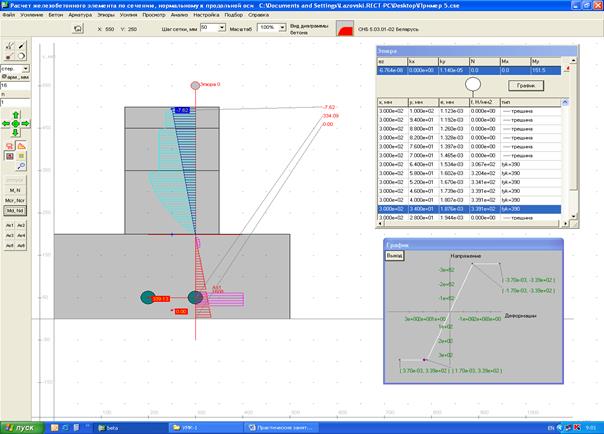
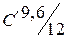
 , установленного при обследовании, имеет согласно проектным данным [8] арматуру в растянутой зоне 4Ø25 мм класса S500 (
, установленного при обследовании, имеет согласно проектным данным [8] арматуру в растянутой зоне 4Ø25 мм класса S500 ( 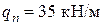 , равномерно распределенной по длине балки пролетом
, равномерно распределенной по длине балки пролетом  .
.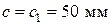 ). В расчетном сечении действует продольная сила
). В расчетном сечении действует продольная сила 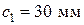 , бетон марки М250, арматура класса А-III: в сжатой зоне – 2Ø20 мм, в растянутой – 2Ø25 мм. При обследовании выявлены в зоне действия максимального изгибающего момента повреждения сжатой зоны в виде отколов ребер (рис. 8) с оголением и коррозией арматуры, а также разрушением мест сварки вертикальной и горизонтальной поперечной арматуры с продольной. Класс конструкции по условиям эксплуатации – ХС3. Требуется проверить прочность балки по нормальному сечению (
, бетон марки М250, арматура класса А-III: в сжатой зоне – 2Ø20 мм, в растянутой – 2Ø25 мм. При обследовании выявлены в зоне действия максимального изгибающего момента повреждения сжатой зоны в виде отколов ребер (рис. 8) с оголением и коррозией арматуры, а также разрушением мест сварки вертикальной и горизонтальной поперечной арматуры с продольной. Класс конструкции по условиям эксплуатации – ХС3. Требуется проверить прочность балки по нормальному сечению ( 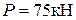 ), а также прогиб и ширину раскрытия трещин, нормальных к продольной оси балки, в зоне действия максимального изгибающего момента от нормативной длительной нагрузки
), а также прогиб и ширину раскрытия трещин, нормальных к продольной оси балки, в зоне действия максимального изгибающего момента от нормативной длительной нагрузки 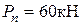 .
.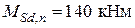 . Требуется произвести расчет конструкции на аварийность.
. Требуется произвести расчет конструкции на аварийность.
 Рис. 8
Рис. 8


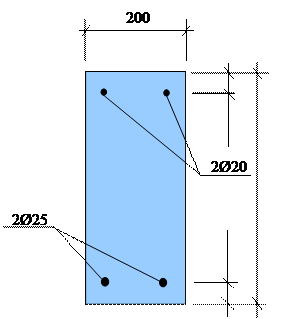 Рис. 9
Рис. 9
 Исходные алгоритмы, рабочие формулы для расчета.Расчетные характеристики кладки для поверочных расчетов эксплуатируемых каменных и армокаменных конструкций определяются в соответствии со схемой рис. 10.
Исходные алгоритмы, рабочие формулы для расчета.Расчетные характеристики кладки для поверочных расчетов эксплуатируемых каменных и армокаменных конструкций определяются в соответствии со схемой рис. 10. , (2)
, (2)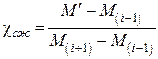 ;
; 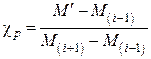 ;
;  ;
; ;
; 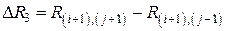 .
.




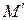
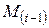


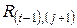
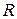
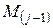
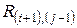

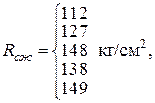
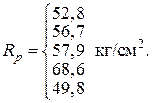
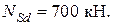
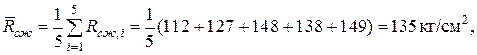
 (табл. 1) – выполняется.
(табл. 1) – выполняется.
 – не выполняется.
– не выполняется.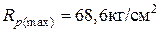 и повторяем расчет:
и повторяем расчет: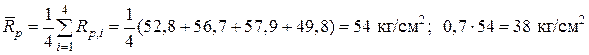 .
.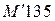 и
и 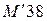 . Далее линейной интерполяцией между ближайшими параметрическими значениями [12, табл. 2] по формуле (2) определяем расчетное сопротивление кирпичной кладки при сжатии:
. Далее линейной интерполяцией между ближайшими параметрическими значениями [12, табл. 2] по формуле (2) определяем расчетное сопротивление кирпичной кладки при сжатии: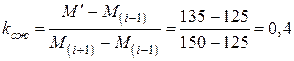 ;
; 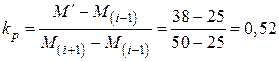 ,
, ;
;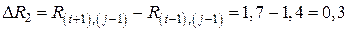 ;
;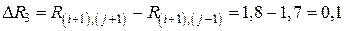 .
.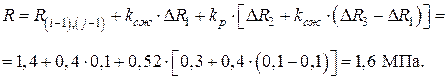
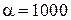 . При минимальном значении гибкости столба
. При минимальном значении гибкости столба 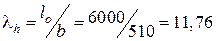 и упругой характеристике
и упругой характеристике 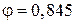 . При наличии силовых трещин, пересекающих менее 4-х рядов кладки,
. При наличии силовых трещин, пересекающих менее 4-х рядов кладки,  .
.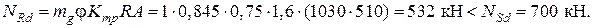
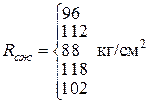 ,
,  .
.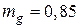 ).
).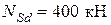 ,
,  , если в процессе эксплуатации он отклонился от вертикали в верхнем сечении в направлении меньшей стороны на 120 мм.
, если в процессе эксплуатации он отклонился от вертикали в верхнем сечении в направлении меньшей стороны на 120 мм.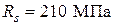 (процент армирования кладки по объему
(процент армирования кладки по объему 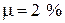 ), в процессе эксплуатации получил повреждения в виде одностороннего разрушения наружного слоя кладки на глубину до половины кирпича. Требуется определить прочность столба при действии длительной нагрузки (
), в процессе эксплуатации получил повреждения в виде одностороннего разрушения наружного слоя кладки на глубину до половины кирпича. Требуется определить прочность столба при действии длительной нагрузки ( 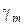 исходя из его нормативного значения, установленного по проектным данным (при их наличии и соответствии им металла эксплуатируемой конструкции) или по результатам статистической обработки испытаний вырезанных образцов по формуле
исходя из его нормативного значения, установленного по проектным данным (при их наличии и соответствии им металла эксплуатируемой конструкции) или по результатам статистической обработки испытаний вырезанных образцов по формуле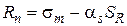 , (3)
, (3)