
|
|
Основные методы интегрирования.Непосредственное интегрирование. Непосредственное интегрирование предполагает использование свойств неопределенного интеграла, таблицы интегралов и различных формул из элементарной математики.
Пример. Решение. Воспользуемся формулой сокращенного умножения (квадрат суммы), свойствами степеней, свойствами 3-4 и формулой 1 таблицы интегралов:
Замена переменной. Пусть требуется найти интеграл с непрерывной подынтегральной функцией Сделаем замену переменных, положив 1) 2) Тогда После интегрирования возвращаются к старой переменной обратной подстановкой. Пример. Решение.
Пример. Решение.
Интегрирование по частям. Интегрированием по частям называется нахождение интеграла по формуле:
где Применяется формула в следующих случаях: 1) Подынтегральная функция является произведением многочлена на показательную или тригонометрическую функцию. Это интегралы вида: В этом случае в качестве Пример. Решение. Подынтегральная функция есть произведение многочлена на тригонометрическую функцию (1 случай). Поэтому в качестве
2) Подынтегральная функция является произведением многочлена на логарифмическую или обратную тригонометрическую функцию. Это интегралы вида: В качестве Пример. Решение. Подынтегральная функция есть логарифмическая функция (2 случай). Поэтому в качестве
Интегрирование рациональных дробей.
Пример. Решение. Сначала разложим дробь на простейшие:
Решая систему, получим: Тогда исходный интеграл примет вид:
Пример. Решение. Так как дробь является неправильной, то сначала выделим целую часть. В результате получим:
Теперь вычислим интеграл:
Пример. Решение. Подынтегральная дробь является правильной, так как степень многочлена в числителе меньше, чем в знаменателе. Разложим дробь на простейшие:
Решая систему, получим: Тогда исходный интеграл примет вид:
Интегрирование тригонометрических выражений. Пример. Решение.
б) Оба числаm, n- четные неотрицательные. Применим формулы:
Пример. Решение.
Интегрирование иррациональных выражений.
Пример. Решение. Сделаем замену
Исходный интеграл сведен к интегралу от рациональной функции – неправильной дроби, которую интегрируем с помощью выделения ее целой части:
Таким образом,
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Если
Пример. Решение.
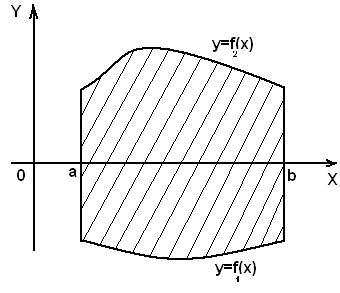
Вычисление площади плоской фигуры, ограниченной линиями, заданными в декартовых координатах. В декартовой системе координат элементарной фигурой является криволинейная трапеция (рис.1), ограниченная линиями
Рис.1
Площадь фигуры (рис.2) вычисляется по формуле:
Рис.2
Пример. Найти площадь фигуры, ограниченной линиями Решение.Построим чертеж к задаче (рис. 3).
Найдем точки пересечения кривых. Для этого решим систему уравнений: Отсюда Площадь фигуры вычислим по формуле:
Рис. 3

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
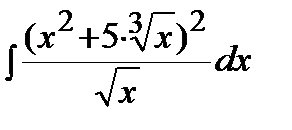 .
.
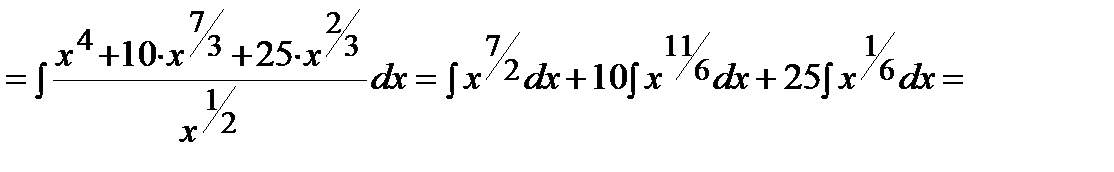
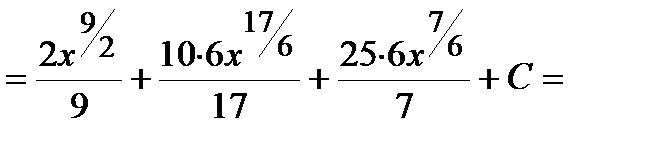
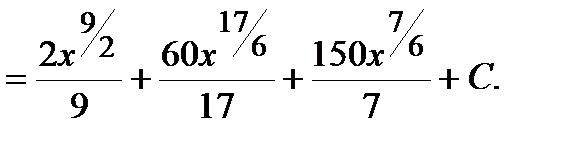
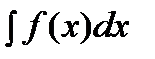 .
. , где функция
, где функция 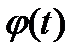 удовлетворяет следующим двум условиям:
удовлетворяет следующим двум условиям: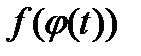 - непрерывная функция;
- непрерывная функция;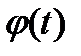 - непрерывно дифференцируемая функция, имеющая обратную функцию.
- непрерывно дифференцируемая функция, имеющая обратную функцию.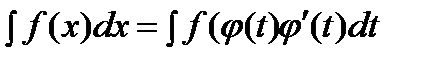 .
.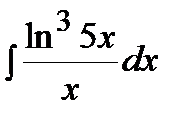 .
. .
.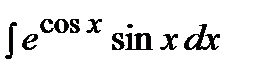 .
.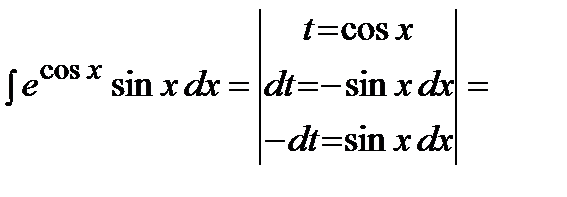
 .
.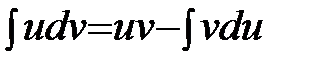 ,
,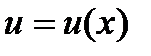
 и
и 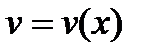 — непрерывно дифференцируемые функции от
— непрерывно дифференцируемые функции от 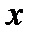 . С помощью этой формулы нахождение интеграла
. С помощью этой формулы нахождение интеграла 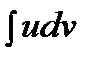 сводится к отысканию другого интеграла
сводится к отысканию другого интеграла  . Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
. Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен. ,
, 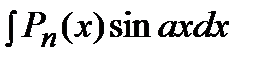 ,
,  .
.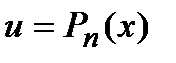 .
. .
.
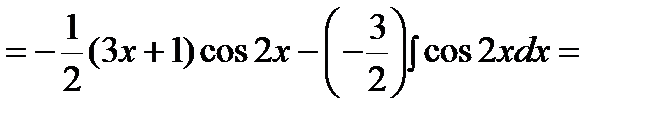
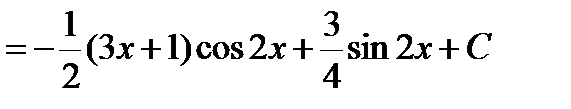 .
. ,
,  ,
,  ,
, 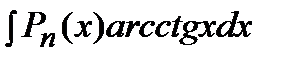 ,
, 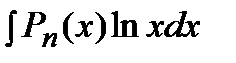 .
.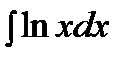 .
.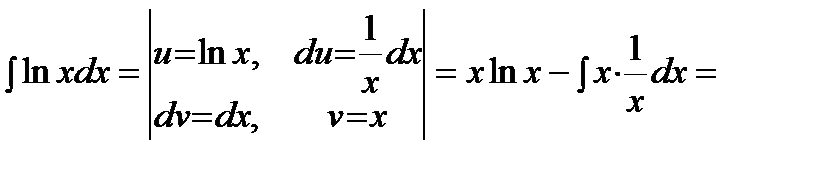
 .
.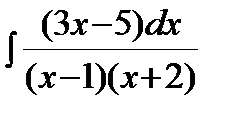 .
.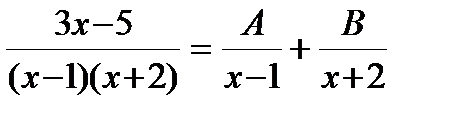 .
.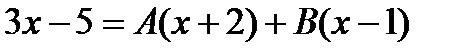 .
. .
.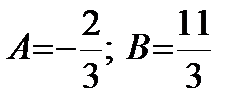 .
.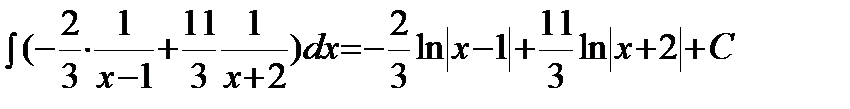 .
.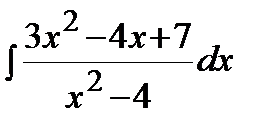 .
. .
.
 .
. .
.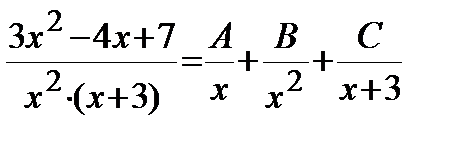 .
.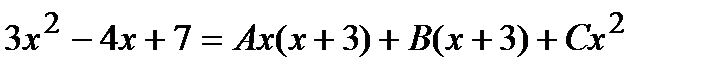 .
.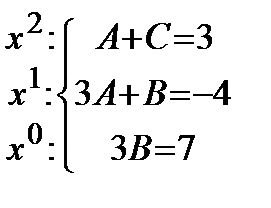 .
.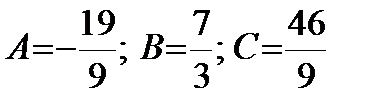 .
. .
. .
.
 .
.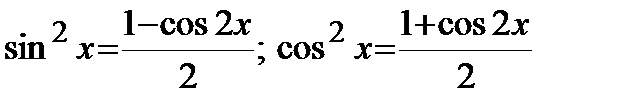 .
. .
.
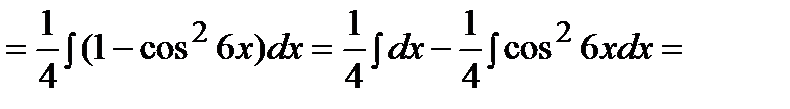
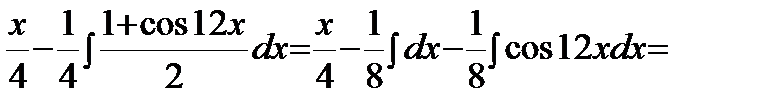
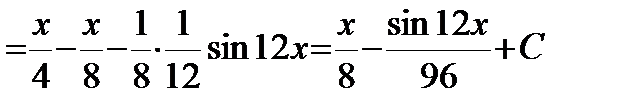 .
. .
. , откуда
, откуда 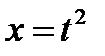 ,
, 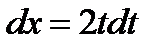 . В результате получим:
. В результате получим: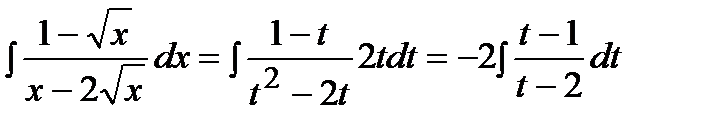 .
.
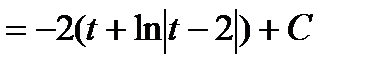 .
. , где
, где 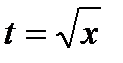 .
. — некоторая первообразная функции
— некоторая первообразная функции 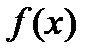 , непрерывной на отрезке
, непрерывной на отрезке 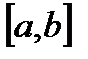 , то определенный интеграл вычисляется по формуле Ньютона – Лейбница:
, то определенный интеграл вычисляется по формуле Ньютона – Лейбница: .
. .
. .
. ,
,  ,
,  ,
,  , площадь которой вычисляется по формуле:
, площадь которой вычисляется по формуле: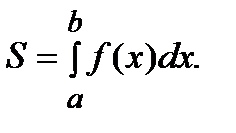


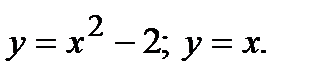
 — это парабола (ветви направлены вверх, вершина находится в точке с координатами (0;-2));
— это парабола (ветви направлены вверх, вершина находится в точке с координатами (0;-2));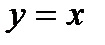 — прямая, проходящая через начало координат.
— прямая, проходящая через начало координат.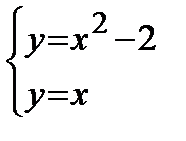 .
.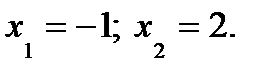
 (кв.ед.).
(кв.ед.).