
|
|
Аналитическое сравнение ФМ и ЧМ.Полученные результаты для наглядности сведем в таблицу. Сопоставляя выражения таблицы 1, легко установить различие между ФМ в ЧМ и обратно ЧМ в ФМ. Таблица 1.
Как видно, при ФМ девиация фазы зависит от амплитуды модулирующего напряжения, но зато девиация частоты зависит от обоих параметров модулирующего сигнала, т.е. от его амплитуды и частоты. При ЧМ, наоборот, девиация частоты зависит только от амплитуды, но зато девиация фазы зависит как от амплитуды, так и от частоты модулирующего напряжения. Если в выражении (2.14) зафиксировать F, то останется только прямая пропорциональность Если в выражении (2.13) зафиксировать F, то Максимальную девиацию фазы при ФМ называют индексом фазовой модуляции
Амплитуду девиации фазы при ЧМ называют также индексом частотной модуляции М:
Методы превращения ФМ в ЧМ и ЧМ в ФМ вытекают из сопоставления накрест лежащих выражений в таблице 1. Формула (4) показывает фактическую зависимость, а формула (1) – требуемую для превращения ФМ в ЧМ. Аналогично для получения ФМ из ЧМ следует формулу (3) превратить в (2). Для простоты математических преобразований предположим, что модулирующий сигнал изменяется по закону синусоиды при ФМ и по закону косинусоиды – при ЧМ. Имеем выражение для текущего значения фазы при ФМ
и для текущего значения частоты при ЧМ
Определим закон изменения частоты при ФМ и фазы при ЧМ. Текущее значение частоты при ФМ получается равным
Выражение перед косинусом представляет собой амплитуду девиации частоты при ФМ
Текущее значение фазы при ЧМ
где
С – постоянная интегрирования; С= В формуле (2.11) выражение перед синусом является амплитудой девиации фазы при ЧМ:
Наибольший интерес представляют выражения (2.10) и (2.12). Переходя в них к циклическим частотам, получим: амплитуда девиации частоты при ФМ
амплитуда девиации фазы при ЧМ
Выражение для мгновенного значения амплитуды ЧМ(ФМ) сигнала при модуляции одним тоном выглядит следующим образом:
где Uн – амплитуда ВЧ сигнала без модуляции (М=0); Iк (М) – функции Бесселя порядка К от аргумента равного индексу модуляции М. Из выражения (2.15) следует, что спектр симметричен (к = Теоретически спектр ЧМ колебания бесконечно широк, но, учитывая монотонное убывание боковых, его можно ограничивать в пределах полосы, определяемой как:
Пчм=2F (1+M+
Для радиовещательных РПДУ с ЧМ максимальная девиация частоты установлена 50 Гц и верхняя граница спектра звукового сигнала F=15 кГц. При этом индекс частотной модуляции М= В системах низовой радиосвязи часто применяют узкополосную ЧМ, имеющую индекс модуляции М Способы осуществления ЧМ
Частотный модулятор изменяется обычно представляет собой транзисторный LC-автогенератор, частота которого под действием модулирующего напряжения с помощью варикапа. Упрощенная (без цепей питания) схема модулятора представлена на рисунке 2.9, а. На этой схеме показаны только реактивные сопротивления, от которых в основном зависит частота колебаний, возникающих в АГ. Элементы С1, С2, С3 и L образуют колебательный контур трехточечного АГ. Конденсатор С4 для тока ВЧ включен последовательно с варикапом, чтобы разделить постоянные напряжения на варикапе и коллекторе транзистора, а при С4 соизмеримой с СВ, обеспечить при необходимости частичное подключение варикапа к контуру АГ. На рисунке 2.9, б представлены характеристики варикапа СВ(е) и действующие на нём напряжения. Напряжение на варикапе e =Eo+
Рис.2.9 Упрощенная схема АГ с ЧМ при помощи варикапа (а), характеристика варикапа и действующие на нем напряжения(б).
Выражение для генерируемой частоты может быть представлено в следующем виде:
где Из приведенного выражения следует, что при ЧМ имеют место два нелинейных явления: изменяется значение центральной частоты на Среднее значение ёмкости возрастает, а частота генератора w понижается. Сдвиг
На рисунке 2.10 представлены основные характеристики для ЧМ (ФМ).
Рисунок 2.10 Основные характеристики при ЧМ (ФМ) модуляции; а-статическая модуляционная; б-амплитудная динамическая модуляционная; в-частотная динамическая модуляционная.
На рисунке 2.11 приведена схема кварцевого АГ управляемого по частоте. В этой схеме КвР используется на частоте последовательного резонанса, как правило, на основной гармонике.
Собственно АГ здесь выполнен по схеме Клаппа, причём ёмкость варикапа является компенсирующей в цепи индуктивного сопротивления, создаваемого L1. Такие АГ обладают несколько пониженной стабильностью генерируемой частоты и не позволяют обеспечить большую девиацию частоты. Поэтому прямые способы осуществления ЧМ в кварцевых АГ находят применение в основном в РПДУ низовой связи. Для повышения стабильности средней частоты применяются системы автоматической подстройки частоты (АПЧ). Получение ЧМ с помощью ФМ (косвенный метод ЧМ) позволяет осуществить управление ВЧ колебаниями не в АГ, а в последующих каскадах, что создаёт хорошие предпосылки в обеспечении высокостабильной работы АГ с КвР. Структурная схема косвенного метода приведена на рисунок 2.12. Преобразование ФМ в ЧМ идет на основании формулы (2.13),
Получение ЧМ с помощью ФМ Практикуется и в РПДУ низовой связи.
Рисунок 2.12 Косвенный метод ЧМ.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 UF (1)
Девиация фазы:
UF (1)
Девиация фазы:
 (3)
(3)
 UF (2)
Девиация частоты:
UF (2)
Девиация частоты:
 (4)
(4)
 UF , т.е. получим ФМ.
UF , т.е. получим ФМ. UF, т.е. получим ЧМ. Следовательно, при модуляции одним тоном нельзя установить примененный вид модуляции; ФМ и ЧМ в этом случае тождественны.
UF, т.е. получим ЧМ. Следовательно, при модуляции одним тоном нельзя установить примененный вид модуляции; ФМ и ЧМ в этом случае тождественны. .
.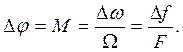
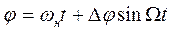 (2.7)
(2.7) (2.8)
(2.8) (2.9)
(2.9) (2.10)
(2.10) (2.11)
(2.11) -основная фаза;
-основная фаза; -дополнительная фаза, появившаяся в результате модуляции;
-дополнительная фаза, появившаяся в результате модуляции; , принимаем
, принимаем  .
.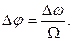 (2.12)
(2.12) ; (2.13)
; (2.13)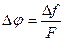 (2.14)
(2.14) (2.15)
(2.15) ); имеет линейную структуру (соседние составляющие отстают друг от друга на одну и туже величину
); имеет линейную структуру (соседние составляющие отстают друг от друга на одну и туже величину  ); амплитуды составляющих спектра определяются функцией Бесселя.
); амплитуды составляющих спектра определяются функцией Бесселя. ). (2.16)
). (2.16) .Тогда требуемая полоса пропускания составит около 180 кГц, что в шесть раз больше аналогичного параметра при АМ (Пам=2Fмакс). Это обстоятельство заставляет использовать ЧМ(ФМ) только в таких ёмких диапазонах, как УКВ, ДМВ и СМВ.
.Тогда требуемая полоса пропускания составит около 180 кГц, что в шесть раз больше аналогичного параметра при АМ (Пам=2Fмакс). Это обстоятельство заставляет использовать ЧМ(ФМ) только в таких ёмких диапазонах, как УКВ, ДМВ и СМВ. 1 и
1 и 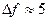 кГц. По своей спектральной характеристики и помехозащищенности она практически не отличается от АМ.
кГц. По своей спектральной характеристики и помехозащищенности она практически не отличается от АМ. e , где Е0-напряжение смещения, соответствующее режиму молчания или “телефонной точке” модуляционной характеристики;
e , где Е0-напряжение смещения, соответствующее режиму молчания или “телефонной точке” модуляционной характеристики; 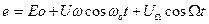

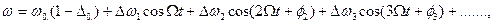
 - относительное смещение центральной частоты при модуляции;
- относительное смещение центральной частоты при модуляции;  - девиации основной частоты модуляции и её гармоник, которые определяются параметрами варикапа, схемы, режимом.
- девиации основной частоты модуляции и её гармоник, которые определяются параметрами варикапа, схемы, режимом. ; возникают нелинейные искажения по второй К2=
; возникают нелинейные искажения по второй К2= 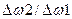 и третьей К3=
и третьей К3=  гармоникам (искажения более высоких порядков малы). Сдвиг центральной частоты объясняется в основном нелинейностью СВ(е); при модуляции приращение ёмкости в положительный полупериод С(+) оказывается больше чем уменьшение её на С(-) в отрицательный полу период модуляции (см. рисунок 2.9,б).
гармоникам (искажения более высоких порядков малы). Сдвиг центральной частоты объясняется в основном нелинейностью СВ(е); при модуляции приращение ёмкости в положительный полупериод С(+) оказывается больше чем уменьшение её на С(-) в отрицательный полу период модуляции (см. рисунок 2.9,б). зависит от UΩ и может быть уменьшен только с помощью линеаризации статической модуляционной характеристики и нелинейного предыскажения модулирующего
зависит от UΩ и может быть уменьшен только с помощью линеаризации статической модуляционной характеристики и нелинейного предыскажения модулирующего 



