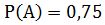|
|
Теория вероятностей и математическая статистика.Дмитровский институт непрерывного образования
К О Н Т Р О Л Ь Н А Я Р А Б О Т А по дисциплине «Теория вероятности»
Выполнил: студент 2 курса группы 0414-МО(з) Поселенцев Олег Андреевич Направления: менеджмент Профиль: организация Дата сдачи _____________ ______________ Подпись
Проверил(а): __________________________ ФИО, ученая степень, ученое звание, должность Дата сдачи ____________ ______________ Подпись
Дмитров, 2016 Оглавление
Что такое теория вероятности и её история. 3 Основные понятия теории. 5 Теория вероятностей и математическая статистика. 6
Что такое теория вероятности и её история.
Тео́рия вероя́тностей — раздел математики, изучающий закономерности случайных явлений:случайные события, случайные величины, их свойства и операции над ними. Возникновение теории вероятностей как науки относят к средним векам и первым попыткамматематического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей[1]. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год)[2]. Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний. В первой половине XIX векатеория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Во второй половине XIX века основной вклад внесли русские учёные П. Л. Чебышёв, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова. Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.
Основные понятия теории.
· Вероятность · Вероятностное пространство · Случайная величина · Локальная теорема Муавра — Лапласа · Функция распределения · Математическое ожидание · Дисперсия случайной величины · Независимость · Условная вероятность · Закон больших чисел · Центральная предельная теорема · Байесовская вероятность Теория вероятностей и математическая статистика.
Задача 8. В круг радиуса Решение.
Пусть событие
Ответ:
Задача 12.
На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет также и в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения. Решение.
Пусть событие
Ответ:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 помещен меньший круг радиуса
помещен меньший круг радиуса  . Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения.
. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения.
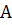 - точка, наудачу брошенная в большой круг, попадет также и в малый круг, тогда вероятность наступления этого события равно отношению площадей малого и большого круга .
- точка, наудачу брошенная в большой круг, попадет также и в малый круг, тогда вероятность наступления этого события равно отношению площадей малого и большого круга .