
|
|
Примеры кодирования простыми блоковыми арифметическими кодамиПример. Пусть алфавит языка состоит из пяти букв: а, в, л, о, с . Их кодирование в цифровую последовательность возможно по правилу:
однозначно декодирует их — если знает правило кодирования. Понятно, что для кодирования всего русского алфавита потребуются уже двузначные десятичные числа, т.е.
или же искажаться
Можно ли восстановить утраченную информацию? — Понятно, что ответ на этот вопрос зависит, в первую очередь, от передающих характеристик самого канала связи. Переходим к кодированию букв в двоичной системе:
по такому каналу? Получатель может увидеть следующие варианты:
но не получит следующие:
Итак, выбор самого экономичного способа кодирования — когда четырем символам алфавита соответствуют четыре двоичных блока — не решает задачу надежной коммуникации. Увеличим длину кода, пусть
Обратим внимание на то, что столбцы не содержат одинаковых блоков. Таким образом, если условие зашумляемости блока не более чем одной ошибкой выполняется, декодер сможет однозначно восстановить передаваемую букву — достаточно будет найти в таблице столбец, содержащий полученный блок. Этот пример служит примером кода, исправляющего ошибки — в данном случае одну ошибку. Что произойдет если зашумленность канала оказывается более высокой, чем предполагалось? Возможны ситуации, когда полученный в результате передачи блок будет содержаться в таблице. Например, если на вход подается блок Определение количества корректирующих символов блоковых кодов При использовании блочных кодов цифровая информация передаётся в виде отдельных кодовых комбинаций (блоков) равной длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга. Почти все блочные коды относятся к разделимым кодам, кодовые комбинации которых состоят из двух частей: информационной и проверочной. При общем числе n символов в блоке число информационных символов равно k, а число проверочных символов r = n – k. К основным характеристикам корректирующих кодов относятся: − число разрешённых и запрещённых кодовых комбинаций; − избыточность кода; − минимальное кодовое расстояние; − число обнаруживаемых или исправляемых ошибок; − корректирующие возможности кодов.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
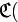 а
а  ,
,  ,
, 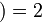 ,
, 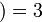 ,
, 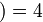 .
.  . Получатель, которому по телефону диктуют цифровые последовательности
. Получатель, которому по телефону диктуют цифровые последовательности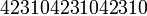 или
или 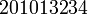
 (и отметим, на всякий случай, что кодирование по правилу
(и отметим, на всякий случай, что кодирование по правилу 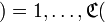 я
я 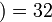 уже не будет правильным…). Пока остановимся на примере пятибуквенного алфавита чтобы показать две проблемы. Предположим, что телефонная линия подвержена помехам и какие-то сообщения могут теряться:
уже не будет правильным…). Пока остановимся на примере пятибуквенного алфавита чтобы показать две проблемы. Предположим, что телефонная линия подвержена помехам и какие-то сообщения могут теряться: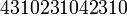

 ,
,  ,
,  ,
,  , забывая пока о пятой букве. Таким образом длина кода
, забывая пока о пятой букве. Таким образом длина кода 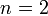 . Предположим, что на каждое передаваемое кодовое слово канал связи дает не более одной ошибки: в каждом блоке длины 2 может менять
. Предположим, что на каждое передаваемое кодовое слово канал связи дает не более одной ошибки: в каждом блоке длины 2 может менять  на
на  или
или 
 или
или  или
или 
 или
или 
 ,
,  ,
,  ,
,  .
. 
 , а канал портит два бита, то получатель может увидеть блок
, а канал портит два бита, то получатель может увидеть блок  , который хоть и содержится в таблице, но декодируется совсем не в ту букву, которая передавалась. А может случиться и так, что на выходе из канала получится блок
, который хоть и содержится в таблице, но декодируется совсем не в ту букву, которая передавалась. А может случиться и так, что на выходе из канала получится блок  , который совсем не содержится в таблице. Эта ситуация иногда более выгодна, чем предыдущая: декодер можно заставить извещать пользователя об обнаружении ошибки в случае когда полученный блок не содержится в таблице. Можно заложить в декодере одновременно обе возможности — сигнализации об ошибке и ее исправления. На примере полученного блока
, который совсем не содержится в таблице. Эта ситуация иногда более выгодна, чем предыдущая: декодер можно заставить извещать пользователя об обнаружении ошибки в случае когда полученный блок не содержится в таблице. Можно заложить в декодере одновременно обе возможности — сигнализации об ошибке и ее исправления. На примере полученного блока 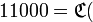 а
а 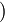 в двух битах, от блока
в двух битах, от блока  в
в  о
о  с
с