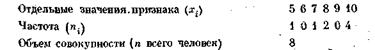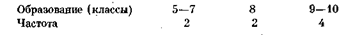Адекватность математических методов.

Одним из основных во­просов, встающих перед исследователем после осуществления измерения, является вопрос о том, какие математические методы он имеет право применять для анализа полученных чисел. Представля­ется целесообразным считать разрешенными (далее допустимыми, адекватными) только такие методы, результаты, применения которых не зависят от того, по какой из возможных шкал получены исходные данные. Необходимым условием такой независимости является инвариантность этих результатов относительно допустимых преоб­разований используемых шкал.

Основанием для такого подхода служит то, что именно такие результаты в принципе поддаются содержательной интерпретации, только они могут отражать реальные закономерности. Отметим, од­нако, что одной независимости результатов применения какого-либо метода от выбора конкретных используемых шкал отнюдь не доста­точно для того, чтобы попытка их содержательной интерпретации увенчалась успехом. Необходимо также содержательное осмысление соответствующих результатов хотя бы для одной из возможных шкал.

Подчеркнем, что понятие допустимости или недопустимости той или иной статистики (различных мер средней тенденции, мер раз­броса, коэффициентов связи между признаками и т. д.) является относительным. Все зависит от того, в каком «контексте», значения этой статистики используются, какие именно соотношения между этими значениями значимы для получения содержательных выводов. Так, сопоставление средних тенденций двух совокупностей может осуществляться с помощью сравнения средних арифметических значений некоторого признака по их величине, с помощью оценки разности (отношения) этих средних и т. д. И возможность исполь­зования средних арифметических значений зависит от того, какие именно соотношения между ними подлежат содержательной интер­претации.

Подчеркнем следующее. Если удалось показать, что некоторое числовое соотношение можно содержательно проинтерпретировать, то не имеет значения, удастся ли при этом найти эмпирические аналоги отдельных входящих в это соотношение операций над чис­лами. Например, можно делать содержательные выводы на основе сравнения по величине двух средних арифметических значений некоторого признака, никак не интерпретируя при этом суммы шкаль­ных значений, вычисляемые в процессе нахождения средних ариф­метических.

Как отмечалось выше, для проверки разрешенное любого со­отношения необходимо убедиться в том, что это соотношение инва­риантно относительно допустимых преобразований использовавшейся при измерении шкалы (или нескольких шкал, если исходные данные получены по разным шкалам, но мы такой случай рассматривать не будем). Однако на практике такая проверка бывает довольно сложной. Соответствующая проблема в теории измерений называ­ется проблемой адекватности рассматриваемого числового соотно­шения. Аналогично можно говорить о проблеме адекватности ре­зультатов применения какого-либо математического метода.

Естественно, что чем уже круг допустимых преобразований, тел большее количество математических соотношений оставляют эти преобразования без изменения. Другими словами, чем выше тип шкалы, чем выше уровень измерения, тем большее количество ма­тематических методов можно применять к шкальным значениям, получая при этом интерпретируемые результаты.

Вопрос об адекватности используемых в социологии математи­ческих методов, как правило, является весьма сложным. Получен­ные к настоящему времени результаты касаются лишь небольшого числа методов. Рассмотрим некоторые из них.

Прежде всего, остановимся на вопросе о корректности использования различного рода средних и коэффициентов связи между признаками.

Ясно, что любую статистику можно использовать в произвольном «контексте» только в том случае, если ее значение остается инва­риантным относительно применения к исходным данным любого допустимого преобразования соответствующей шкалы. Нетрудно показать, что для номинальной шкалы, удовлетворяющей такому условию, средней будет мода, для порядковой шкалы — медиана и другие квантили. Значение среднего арифметического остается без изменения лишь для абсолютных шкал. Поэтому обращение с ним требует известной осторожности. Однако можно показать¹¹, что сравнивать по величине средние арифметические значения какого-либо признака можно уже в том случае, когда исходные данные получены по интервальной шкале (другими словами, результаты такого сравнения не изменяются при применении к исходным данным произвольного положительного линейного преобразования).

Относительно коэффициентов связи можно сказать следующее, Инвариантными относительно допустимых преобразований рассматриваемых шкал являются значения коэффициентов связи, рекомендуемых в § 6 настоящей главы для соответствующего уровня изме­рения. Так, значение коэффициента корреляции не изменяется при применении к исходным данным произвольного положительного линейного преобразования; значения коэффициентов Кендалла t и Спирмена r, инвариантны относительно произвольного монотонно возрастающего преобразования входящих в них величин; значения коэффициентов х²> Ф Р, К, Т инвариантны относительно произвольного взаимно однозначного преобразования исходных данных¹².

Группировка материала статистических наблюдений

Измеряя характеристики объекта, исследователь собирает пер­вичный статистический материал. Дальнейшая его задача состоит в систематизации и обобщении результатов измерения для выявле­ния характерных черт, существенных свойств тех или иных типов Явлений, обнаружения закономерностей изучаемых процессов и про­верки гипотез, лежащих в основе исследования. В основе исполь­зуемых методов обработки полученных материалов исследования лежит предварительное упорядочение первичных данных главным образом при помощи статистической группировки и составления статистических таблиц.

Статистическая группировка.

Распределение изучаемой совокуп­ности на однородные группы по существенным для нее признакам (характеристикам) называется статистической группировкой.

Основное назначение группировки состоит, во-первых, в уста­новлении численности каждой отдельно взятой части совокупности, расчленённой в соответствии со значениями определенного признака (или нескольких признаков), и, во-вторых, в изучении влияния причин и зависимости явлений.

Главным вопросом метода группировки является правильный выбор группировочных признаков. Могут быть получены превосход­ные данные, по эти сведения пропадут совсем, если их группировка будет произведена неправильно. Поэтому при выборе признаков для отграничения явлений одного типа от явлений других типов необхо­димо руководствоваться не субъективными построениями, а содер­жательным анализом особенностей социальных явлений, задачами исследования, а также видом признаков, с которыми имеет дело исследователь. Основные группировки должны тщательно разрабатываться уже при составлении программы социологического исследования с необходимостью отражать ключевые гипотезы.

Ряды распределения.

Результат группировки единиц наблюдения по какому-либо признаку называется статистическим рядом. Обозначим группировочный признак х. Пусть это будет уровень образова­ния каждого человека в данном списке лиц. Получим неупорядочен­ный ряд результатов отдельных наблюдений: 10, 5, 7, 8, 10, 10 10 (классы). Если отдельные наблюдения расположить в порядке воз­растания указанных выше значений признака, то получим вариаци­онный ряд: 5, 7, 8, 10, 10, 10, 10.

По вариационному ряду количественного признака можно под­считать, как часто каждое значение этого признака встречается в совокупности. В результате получим частотное распределение для данного признака. Иногда его называют эмпирическим или стати­стическим распределением.Для вышеприведенного примера частотное распределение выглядит так:

Условимся каждое, отдельное значение признака х обозначать х₁, х₂,… , x_k (в данном примере это 5, 7, 8, 9 и 10 классов).

Абсолютное число, показывающее, сколько раз встречается то или иное значение признака х, называется частотой и обозначается соответственно n₁, n₂, ..., n_k.

Относительной частотой называется доля значений признака в общем числе наблюдений и обозначается m₁, .,., m_k.

Например, для приведенного частотного ряда частота наиболь­шего значения признака (10 классов) равна 4, а относительная частота m₅ = 4/8 = 0,5. Относительную частоту обычно выражают в процентах (m_k = 50%).

Сгруппированные данные. Как правило, для последующей статистической обработки или более наглядного представления данных отдельные значения признаков объединяются в группы (интервалы). В этом случае частоты соотносят уже не с каждым отдельным зна­чением признака, как это делалось в предыдущем примере, а с ря­дом значений, попадающих в определенный интервал.

Например, распределение уровня образования в вышеприведенном примере может быть представлено в виде интервального ряда следующим образом:

Частотное распределение с не сгруппированными значениями иногда называют дискретным рядом распределения.

При построении интервальных рядов большое значение имеет выбор типа, количества и размеров интервалов. Общее требование к этому выбору состоит в том, что группировка должна наиболее полно выявлять существенные свойства рядов распределения.

Существующие формальные правила выбора оптимальной вели­чины интервалов редко оказываются полезными при работе с социо­логическими данными¹³. Как правило, приходится делать выбор между двумя крайностями: слишком крупные интервалы для дан­ного объема выборки скрадывают многие нюансы в описании явле­ния, а слишком дробные ведут к статистически незначимым малым частотам внутри интервала.

Интервальные ряды распределения могут строиться с равными и неравными интервалами. Неравные интервалы применяются при неравномерном распределении частот значений группировочного признака — для выделения качественно отличных типов явлений. Например, выбор интервалов при группировке данных распределения совокупности опрошенных по возрасту можно основываться на этапах жизненного цикла. При группировке семей по признаку «число книг в семье», опираясь на информацию ранее проведенных исследований о том, что чаще всего встречаются библиотеки с чис­лом книг по 500 и реже — библиотеки, насчитывающие 10000 книг, целесообразно установить неравные интервалы группировки, напри­мер такие: 1—50, 51—100, 101—200, 201—300, 301—500, 501—700, 701-1000, 1001-2000, 2001—5000, 5001-10000.

Если у исследователя нет предварительной информации, о харак­тере распределения по тому или иному признаку, то следует зада­вать равные интервалы. Равные интервалы также наиболее удобны при использовании методов математической статистики. Опыт пока­зывает, что по каждому из признаков не следует брать более 20 группировочных интервалов.

При образовании интервалов необходимо точно обозначить коли­чественные границы группы, избегая таких обозначений границ интервалов, при которых отдельные единицы совокупности могут быть отнесены в две соседние группы. Поэтому, как правило, необ­ходимы дополнительные указания о том, считать ли граничные значения интервалов «включительно» или «исключительно».

Довольно часто социологу приходится сталкиваться с ситуацией, когда необходимо провести перегруппировку материала, задав дру­гие интервалы, но нет возможности при этом обратиться к перво­начальным статистическим данным.

При расщеплении интервала на несколько частей приходится вводить априорное предположение о частотном распределении внут­ри интервала, поскольку истинное распределение неизвестно. Самым простым является предположение о равномерности частотного рас­пределения по отдельным значениям признака. Другие формы распределения требуют достаточно громоздких вычислений¹⁴.

Статистические таблицы.

Предусмотренные программой исследо­вания и методиками обработки группировки объектов по каждому из признаков кладутся в основу статистических таблиц, обобщаю­щих исходные данные.

В дальнейшем составляют более сложные таблицы, позволяющие сопоставлять ряды распределений, и, наконец, комбинационные таблицы, в которых три или более признака перекрещиваются, ком­бинируются. По таким таблицам устанавливаются, измеряются и анализируются связи между признаками исследуемой совокупности объектов.

Построение таблицы подчинено определенным правилам. Основ­ное содержание таблицы должно быть отражено в названии (круг рассматриваемых вопросов, географические границы статистической совокупности, время, единицы измерения).Таблицы бывают простые, групповые и комбинационные.

Простые таблицы представляют собой перечень, список, отдельных единиц совокупности о количественной (или качественной) характеристикой каждой из них в отдельности.

В групповых таблицах содержится группировка единиц совокуп­ности по одному признаку, а в комбинационных — по двум и более признакам.

Примером комбинационной разработки статистической таблицы может служить табл. 1.

Такая таблица представляет собой нечто гораздо большее, чем простой перечень данных, она является способом и вместе с тем результатом определенной организации данных. Хорошо сконструи­рованная таблица позволяет исследователю более четко представить и описать смысл и сущность изучаемого им социального явления.

Таким образом, метод группировки и представление материала в виде статистических таблиц уже дают определенные возможности для изучения социологических данных. С другой стороны, он является совершенно необходимым средством для дальнейшего анализа и применения более тонких статистических методов.

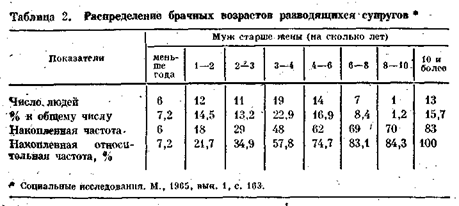
3. Графическая интерпретацияэмпирических зависимостей

Частотные распределения изображаются также в виде диаграмм и графиков. Главным достоинством графического изображения яв­ляется его наглядность.

Графическая интерпретация эмпирических зависимостей осно­вана на знании технических правил построения рядов, типов и свойств теоретических распределений. Здесь мы рассмотрим графика вариационных рядов: гистограмму, полигон и кумуляту распределения.

Гистограмма.

Гистограмма — это графическое изображение интервального ряда. По оси абсцисс откладывают границы интервалов, на которых строят прямоугольники с высотой, пропорциональной плотностям распределения соответствующих интервалов (пропор­циональной числу единиц совокупности, приходящейся на единицу длины интервала). При равных интервалах плотности распределения пропорциональны частотам, которые и откладываются по оси ординат (рис. 1, табл. 2).

На гистограмме общее число лиц в каждой категории выражает­ся площадью соответствующего прямоугольника, а общая площадь равна численности совокупности (так как гистограмма на рис. 1 строится по относительным частотам, то площадь равна единице (100%). Поэтому для интервалов 4—6, 6—8, 8—10 в табл. 2, которые в 2 раза больше предыдущих, нужно брать высоты прямоугольников в 2 раза меньшие. При нанесении на графикепоследне­го открытого интервала

«10 лет и более» условно будем считать верхней его границей 40 лет. Тогда ширина интервала равна 30го­дам, а плотность распределения — около 0,5% (15,7 : 30 ~ 0,5).

Полигон распределения.

Для построения полигона величина при­знака откладывается на оси абсцисс, а частоты или относительные частоты — на оси ординат. Из точек, соответствующих значениям признака, восстанавливаются перпендикуляры, равные по высоте частотам. Вершины перпендикуляров соединяются прямыми ли­ниями.

Для интервального ряда ординаты, пропорциональные частоте (или относительной частоте) интервала, восстанавливаются перпен­дикулярно оси абсцисс в точке, соответствующей середине данного интервала.

Следующие данные распределения рабочих в возрасте до 24 лет по тарифным разрядам (высококвалифицированные рабочие сельхоз-машиностроения)¹⁵ дают возможность построить полигон распределе­ния (рис. 2):

Условно принято крайние ординаты признака соединять с серединами примыкающих интервалов (на рис. 2 эти замыкающие линии нанесены пунктиром). Однако для распределения, где концентрация событий увеличивается на концах полигона, такое изображение мо­жет привести к ложным представлениям о существе явления.

Кумулята.

Для графического изображения вариационных рядов используются также кумулятивные кривые. При построении кумуляты, как и гистограммы, на оси абсцисс откладываются границы интервалов (либо значения дискретного признака), а на оси орди­нат — накопленные частоты (либо относительные частоты), соответ­ствующие верхним границам интервалов. Таким образом, отличие кумуляты от гистограммы в том, что на графике кумуляты столби­ки, пропорциональные частотам, последовательно накладываются один на другой, так что высота последнего столбика является сум­мой высот столбиков гистограммы.

Кумулята округляет индивидуальные значения признака в пре­делах интервала и представляет собой возрастающую ломаную линию.

Кумулята позволяет быстро определить процент лиц, находящихся ниже или выше заданной величины признака. Например, по данным табл. 3, процент семейств, в которых муж старше cyпруги не более чем на 5 лет, равен 65 (рис. 3, точка А).

Не нашли, что искали? Воспользуйтесь поиском по сайту: