
|
|
К задаче линейного программированияСведение матричной игры
Предположим, что цена игры положительна ( γ > 0). Если это не так, то согласно свойству смешанных стратегий (теорема 3) всегда можно подобрать такое число а, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и, следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются. Итак, пусть дана матричная игра с матрицей А порядка m х n.Согласно основной теореме матричных игр и теореме об активных стратегиях оптимальные смешанные стратегии P=(p1, ..., pm), Q= (q1, ..., qn) соответственно игроков 1 и 2 и цена игры γдолжны удовлетворять соотношениям:
Разделим все уравнения и неравенства в (1) и (2) на ν (это можно сделать, т.к. по предположению ν > 0) и введём обозначения :
Тогда (1) и (2) перепишется в виде :
Поскольку первый игрок стремится найти такие значения pi и, следовательно, ui , чтобы цена игры была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений ui
Поскольку второй игрок стремится найти такие значения qj и, следовательно, xj , чтобы цена игры была наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений xj,
Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП). Решив эти задачи, получим значения ui
Таким образом, процесс нахождения решения матричной игры с использованием методов линейного программирования состоит из следующих этапов: 1. Если в исходной платежной матрице А есть отрицательные элементы или нули, то необходимо добавить ко всем элементам матрицы одно и то же достаточно большое положительное число C, так, чтобы все элементы матрицы 2. Составить пару двойственных задач линейного программирования, эквивалентных полученной матричной игре. 3. Определить оптимальные планы пары двойственных задач. 4. Используя соотношение между планами пары двойственных задач и оптимальными стратегиями и ценой игры, найти решение игры, заданной матрицей 5. Перейти к оптимальным смешанным стратегиям и цене игры с матрицей А,
Пример. Найти решение игры, определяемой матрицей.
Решение. При решении этой игры к каждому элементу матрицы А прибавим 1 и получим следующую матрицу
Составим систему уравнений (1) и (2):
Разделим каждое из неравенств и уравнений, входящих в системы (1) и (2) на γ и введём новые переменные u1, u2, u3; и x1 , x2 , x3
Составим пару двойственных задач линейного программирования:
Решение обеих задач можно найти с помощью двойственных симплекс-таблиц. Вспомним правила метода МЖИ: 1. Разрешающий элемент заменяется обратной величиной. 2. Все элементы разрешающей строки делятся на разрешающий элемент. 3. Все элементы разрешающего столбца делятся на разрешающий элемент, и меняется знак на противоположный. 4. Все остальные элементы таблицы считаются по правилу прямоугольника и делятся на разрешающий элемент, т. е. элемент который необходимо посчитать умножается на разрешающий и вычитается произведение элементов стоящих на противоположной диагонали (см. таб. №1), затем полученное число делится на разрешающий элемент. Определяется разрешающий элемент следующим образом: 1. Из отрицательных элементов сроки Z выбирается наибольший элемент по модулю (кроме столбца свободных членов). 2. К выбранному столбцу составляется симплексное отношение (столбец свободных членов делится на выбранный столбец). 3. Из элементов симплексного отношения выбирается положительный минимальный элемент. 4. На пересечении выбранного столбца и строки находится разрешающий элемент.
Результаты расчёта:
Замечание. Для того, чтобы найти решение двойственных задач надо повторить симплексный метод решения задач линейного программирования

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|





 ,
, 
 ,
, ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , ui ≥ 0,
, ui ≥ 0, 
 ,
,  , xj ≥ 0 ,
, xj ≥ 0 , 

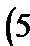
 были положительными.
были положительными. .
. .
.

 (1)
(1)  (2)
(2)

 → max
→ max


 ,
,  ,
,  =
= 