Построение детерминированных анализаторов (разбор снизу-вверх)

Грамматики простого предшествования (ГПП)

< ^о , = ^о , ^о > - три вида отношений. Не более одного отношения для любой пары символов.

Если между символом стека и очередным входным сиvволом выполнить отношение < ^о = ^о, то выполняется перенос.

^о > Это значит, что верхняя часть стека содержит выражения и выполняется свертка.

Алгоритм перенос-свертка:

Сначала в стек помещается ограничитель.

Для определенности будем считать, что для любого нетерминального и терминального символа будет выполняться _|_ < ^о А.

Будем считать, что после входной цепочки помещается _|_ и для любого нетерминального и терминального символа будет выполняться А ^о > _|_

Процесс будет продолжаться до тех пор, пока цепочка не свернется к начальному символу S. Следующим за ним в стеке будет стоять _|_.

A < ^о B – правая часть начинается с B.

B=C=…=D – находимся в правой части

С ^о > K – где К – символ в входной цепочке.

Если = ^о или < ^о .то осуществляется перенос, т.е. входной символ записывается в стек.

Иначе, если верхняя часть стека содержит всю правую часть, то осуществляется свертка.

Для работы алгоритма нужна таблица построения отношений.

Каждое отношение определяется не для каждой пары символов.

Отношения Вирта-Вебера

V →…AB…

1. = ^о – если существует хотя бы одно правило вида А = ^о В, где А и В – терминальные/нетерминальные символы. Иначе отношение не существует.

2. А< ^о В Существует тогда и только тогда, когда существует порождающее правило вида V→…AW. W выводится за 1 и более шагов. Цепочка начинается с символа В. W=>⁺B…

3. А ^о> В Существует правило вида V →…UW… Где U – терминал, из которого можно вывести цепочку, заканчивающуюся на символ А U=>⁺…А

W либо совпадает с В, либо состоит из нетерминала (всегда!), из которого можно вывести цепочку, начинающуюся с В. W=>^*B…

First - элементарное отношение. Оно, как и last легко выводится просмотром правил:

КС-грамматика называется обратимой, если не существует двух таких порождающих правил, что в их левых частях стоят различные нетерминалы, а в правых – одинаковые.

Грамматика называется ГПП, если отношения заданы правильным образом и обратимы.

Свойство обратимости не такое уж строгое ограничение, т.е. если грамматика не обратима, то ее можно привести к обратимой.

Грамматика, которая является обратимой и в которой допускаются одновременно отношения < и =, но не допускаются одновременно отношения > и какое-либо другое, называется грамматикой нестрогого предшествования.

Преобразования грамматики нестрогого предшествования:

Введем дополнительный нетерминал и преобразуем правила:

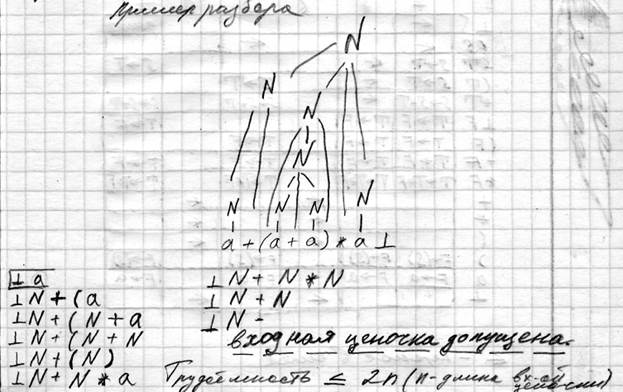
Трудоемкость: n*m, где n – длина входной цепочки, m-количество нетерминальных символов.

Операторное предшествование ОП

A →…UV.. по аналогии с НФГ.

Отношение предшествования

Задается только для 2х терминальных символов

< ^о , = ^о , ^о >

_|_ < ^о a

a ^о > _|_

Мы не можем воспроизвести здесь цепочные сворачивания. Чтобы ликвидировать эту проблему, придумано, что все нетерминальные символы, помещаемые в стек являются неразличимыми. Поэтому не нужно делать цепочных сворачиваний. Явные сворачивания будем применять к тем правым частям, которые содержат хотя бы один терминальный символ.

a= ^о b V→…ab… или V→…aWb…

a< ^о b V→…aU… U=>⁺b… или U=>⁺Wb… (first*)(firstterm)

a ^о > b V→…Ub… U=>⁺…a или U=>⁺…aW (last*)(lastterm)

Пример

S→S+T|T

T→T*F|F

F→(S)|a

Преимущества: трудоемкость не превышает 2n, более компактное дерево; недостатки: охват класса грамматик менее мощный, чем у других методов. Из-за обезличивания нетерминальных символов. Мы в итоге используем более широкий язык, чем заданный.

LR(k)-грамматики

Будут производиться перенос и свертка.

На каждом шаге анализируется не более чем k терминальных символов. И столько верхних символов, сколько необходимо для обеспечения однозначности действия анализатора. Минимальное разумное значение k=1.

Простейший анализатор такого типа: LR(1).

Этот метод наиболее мощный из всех рассмотренных.

Метод очень громоздок, так что рассмотрим на примере простейшей грамматики:

Пример

S→S+T|T

T→T*F|F

F→(S)|a

_|_, выход: _|_

← - перенос

Иногда необходимо будет анализировать по 2 верхних символа (обычно это бывает, если верхний символ - нетерминальный, если терминальный – достаточно одного).

Трудоемкость в худшем случае mn (число нетерминальных символов * длину входной цепочки)

Не нашли, что искали? Воспользуйтесь поиском по сайту: