
|
|
Статистическое оценивание.
Пусть имеется некоторая генеральная совокупность, каждый объект которой наделен количественным признаком X. При случайном извлечении объекта из генеральной совокупности становится извлеченным значение x признака X этого объекта. Таким образом, можно рассматривать извлечение объекта из генеральной совокупности как испытание, X – как случайную величину, а x – как одно из возможных значений X. Допустим, что из теоретических соображений удалось установить, к какому типу распределений относится признак X. Естественно, возникает задача оценки (приближенного нахождения) параметров, которыми определяется это распределение. Обычно в распоряжении имеются лишь данные выборки генеральной совокупности, например, значения количественного признака x1, x2, …, xn, полученные в результате n наблюдений. Через эти данные и выражается оцениваемый параметр. Статистической оценкой Оценки параметров подразделяются на точечные и интервальные. Точечные оценки задаются одним числом, интервальные – границами доверительного интервала. Точечные оценки должны удовлетворять определённым требованиям. Несмещенной называется точечная оценка Оценка Несмещенной и состоятельнойоценкойматематического ожидания является выборочная средняя: Несмещенной и состоятельной оценкой дисперсии является исправленная выборочная дисперсия: Несмещенной и состоятельной оценкой среднего квадратического отклонения является корень из несмещённой оценки дисперсии: При большом числе опытов точечная оценка, как правило, близка к неизвестному параметру. Если же число наблюдений мало, то случайный характер величины Интервал Интервальной оценкой (с надежностью g ) математического ожидания ---------------------------------------------------------------------------------------------------------------- Статистическое оценивание. Стр. 1 при известном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал Интервальной оценкой (с надежностью g ) математического ожидания ТАБЛИЦА ЗНАЧЕНИЙ
Задачи для самостоятельного решения. №1. В итоге пяти измерений некоторой детали получены следующие результаты (в мм): 52, 54, 53, 55, 56. Найти несмещённые оценки для математического ожидания, дисперсии, среднего квадратического отклонения. №2. Найти доверительный интервал для оценки с надёжностью 0,99 неизвестного математического ожидания нормально распределённого признака Х генеральной совокупности, если объём выборки равен 25, выборочное среднее равно 16,8, а среднее квадратическое отклонение генеральной совокупности равно 5.
№3. Из генеральной совокупности извлечена выборка
Найти доверительный интервал для математического ожидания с надёжностью 0,95.
---------------------------------------------------------------------------------------------------------------- Статистическое оценивание. Стр. 2 Домашнее задание к практической работе №12.
№1. Из генеральной совокупности извлечена выборка
Найти несмещённые оценки генерального среднего и дисперсии. №2. Найти доверительный интервал для оценки с надёжностью 0,95 неизвестного математического ожидания нормально распределённого признака Х генеральной совокупности, если объём выборки равен 50, выборочное среднее равно 20, а генеральное среднее квадратическое отклонение равно 6. №3. Произведено 5 независимых опытов над СВ Х, распределённой нормально. Получены следующие результаты опытов: -25, -20, 10, 21, 34. Найти доверительный интервал для математического ожидания с надёжностью 0,99.
---------------------------------------------------------------------------------------------------------------- Статистическое оценивание. Стр. 3 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 параметра
параметра  распределения называется приближённое значение параметра, вычисленное по результатам выборки.
распределения называется приближённое значение параметра, вычисленное по результатам выборки.
 .
.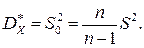
 .
. может привести к значительному расхождению между
может привести к значительному расхождению между  так, чтобы вероятность поглощения этим интервалом параметра q, т.е. вероятность двойного неравенства
так, чтобы вероятность поглощения этим интервалом параметра q, т.е. вероятность двойного неравенства 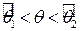 была не меньше заданного числа g.
была не меньше заданного числа g.
 если неравенство
если неравенство 
 нормально распределенного количественного признакаX по выборочной средней
нормально распределенного количественного признакаX по выборочной средней 
 где t – значение аргумента функции Лапласа Ф(t), при котором
где t – значение аргумента функции Лапласа Ф(t), при котором  n – объем выборки.
n – объем выборки.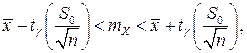 где
где  находят по таблице значений
находят по таблице значений  по заданным n и g .
по заданным n и g .





