
|
|
Административная работа 1 по математике. ЕГЭ-МАТЕМАТИКА. Профиль.Административная работа 1 по математике. ЕГЭ-МАТЕМАТИКА. Профиль. ВАРИАНТ 001. 1. После понижения цены на 20% рубашка стала стоить 680 рублей. На сколько рублей рубашка подешевела? 2. На рисунке изображен график осадков в г. Калининграде с 4 по 10 февраля 1984 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм. Определите по рисунку, сколько дней из данного периода выпадало от 2 до 8 мм осадков.
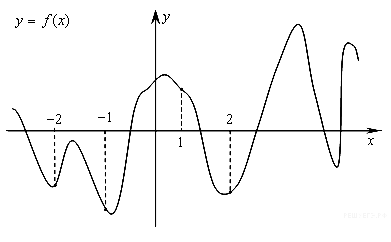
3. Какой угол образует часовая и минутная стрелки в 16:30? 4. Каждая нечетная лампочка новогодней гирлянды работает по циклической схеме: первые 2 секунды горит, а следующие две секунды не горит. Каждая четная лампочка циклично горит первые три секунды, потом две секунды не горит. В момент включения гирлянды в сеть загораются все лампочки. Какова вероятность, что, зайдя в комнату, Ваня увидит горящими все лампочки на новогодней гирлянде? 5. Решите уравнение 6. В прямоугольном треугольнике ABC с прямым углом B проведена медиана BM, равная 5. AB=8. Найдите площадь треугольника ABC. 7. На рисунке изображен график некоторой функции f(x) и отмечены точки −2, −1, 1, 2. В скольких точках из четырех указанных производная отрицательна?
8. Центры всех граней правильного тетраэдра SABC являются вершинами нового тетраэдра S1A1B1C1. Площадь поверхности тетраэдра SABC равна 27. Найдите площадь полной поверхности S1A1B1C1 ? 9. Упростите выражение 10. Водолазный колокол, содержащий υ = 2 моля воздуха при давлении p1 = 1,75 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления p2. Работа, совершаемая водой при сжатии воздуха, определяется выражением 11. Двое велосипедистов одновременно выехали из пункта A в пункт B, расстояние между которыми равно 120 км. Известно, что скорость первого велосипедиста на 8 километров в час больше второго. После прибытия в пункт B первый велосипедист тут же развернулся и встретился со вторым велосипедистом спустя 7,5 часов после старта. На каком расстоянии от пункта B встретились велосипедисты? 12. Найдите точку максимума функции _____________________________________________________________________________ 13. А) Решите уравнение Б) Найдите корни этого уравнение в промежутке 14. В правильной четырехугольной пирамиде SABCD с вершиной S построено сечение плоскостью AKL, где точка К – середина ВС, точка L взята на ребре SB так, что SL:LB=2:1. А) Докажите, что ребро SD параллельно плоскости сечения. Б) Найдите угол между плоскостью сечения и плоскостью основания пирамиды, если все рёбра пирамиды равны. 15. Решите неравенство 16. В равнобокой трапеции ABCD с основаниями AD и BC в угол A и угол B вписаны окружности равных радиусов, касающиеся друг друга внешним образом. А) Доказать, что прямая, соединяющая центры этих окружностей, параллельна боковой стороне AB. Б) Известно, что расстояние между центрами этих окружностей составляет 1/2 длины стороны AB. Найдите косинус угла BAD трапеции. 17. Ключевой ставкой Центрального банка (ЦБ) РФ называется ставка, по которой ЦБ кредитует коммерческие банки. В настоящее время ставка ЦБ равна 11% годовых. Некоторый ипотечный банк пускает деньги, заимствованные у ЦБ в оборот, предлагая населению кредитные продукты с фиксированной ставкой 14% годовых. Согласно статистическим наблюдениям, если банк одобрит n% (n>0) заявок на ипотеку, то получит (1+0,05n)% проблемных должников (не выплачивающих ипотеку). Какой целочисленный процент кредитных заявок следует одобрять ипотечному банку, чтобы максимизировать операционную прибыль, если размер выручки пропорционален проценту одобренных заявок, помноженному на средний процент прибыли банка от всех кредитных договоров? 18. Найдите все значения параметра a, при которых решением неравенства
19. У Пети на счету 400$. Раз в месяц Петя либо кладет на счет 30$, либо снимает 69$. А) Мог ли в какой-то момент времени баланс Пети равняться нулю? Б) Какой минимальный остаток средств мог оказаться на счету Пети? В) За какое минимальное количество транзакций (пополнений и снятий) может быть достигнут этот минимальный остаток? Административная работа 1 по математике. ЕГЭ-МАТЕМАТИКА. Профиль. ВАРИАНТ 002. 1. После понижения цены на 30% рубашка стала стоить 630 рублей. На сколько рублей рубашка подешевела? 2. На рисунке изображен график осадков в г. Калининграде с 4 по 10 февраля 1984 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм. Определите по рисунку, сколько дней из данного периода выпадало менее 4 мм осадков.
3. Какой угол образует часовая и минутная стрелки в 14:30? 4. Каждая нечетная лампочка новогодней гирлянды работает по циклической схеме: первые 2 секунды горит, а следующую одну секунду не горит. Каждая четная лампочка циклично горит первые три секунды, потом две секунды не горит. В момент включения гирлянды в сеть загораются все лампочки. Какова вероятность, что, зайдя в комнату, Ваня увидит горящими все лампочки на новогодней гирлянде? При необходимости, округлите ответ до сотых. 5. Решите уравнение 6. В прямоугольном треугольнике ABC с прямым углом B проведена медиана BM. AB=8. Площадь треугольника ABC равна 60. Найдите длину медианы BM. 7. На рисунке изображен график некоторой функции f(x) и отмечены точки −2, −1, 1, 2. В скольких точках из четырех указанных производная положительна?
8. Центры всех граней правильного тетраэдра SABC являются вершинами нового тетраэдра S1A1B1C1. Объём тетраэдра SABC равен 243. Найдите объём тетраэдра S1A1B1C1 ? 9. Упростите выражение 10. Для поддержания навеса планируется использовать цилиндрическую колонну. Давление 11. Двое велосипедистов одновременно выехали из пункта A в пункт B, расстояние между которыми равно 60 км. Известно, что скорость первого велосипедиста на 8 километров в час больше второго. После прибытия в пункт B первый велосипедист тут же развернулся и встретился со вторым велосипедистом спустя 3 часа 45 минут после старта. На каком расстоянии от пункта А встретились велосипедисты? 12. Найдите наименьшее значение функции _____________________________________________________________________________ 13. А) Решите уравнение Б) Найдите корни этого уравнение в промежутке 14. В правильной четырехугольной пирамиде SABCD с вершиной S построено сечение плоскостью AKL, где точка К – середина ВС, точка L взята на ребре SB так, что SL:LB=1:2. А) Докажите, что высота пирамиды SO параллельна плоскости сечения. Б) Найдите площадь сечения, если все рёбра пирамиды равны 1. 15. Решите неравенство 16. В равнобокой трапеции ABCD с основаниями AD и BC в угол A и угол B вписаны окружности равных радиусов, касающиеся друг друга внешним образом. А) Доказать, что прямая, соединяющая центры этих окружностей, параллельна боковой стороне AB. Б) Известно, что расстояние между центрами этих окружностей составляет 1/3 длины стороны AB. Найдите синус угла ABC трапеции. 17. Ключевой ставкой Центрального банка (ЦБ) РФ называется ставка, по которой ЦБ кредитует коммерческие банки. В настоящее время ставка ЦБ равна 11% годовых. Некоторый банк пускает деньги, заимствованные у ЦБ в оборот, предлагая населению кредитные продукты с фиксированной ставкой 20% годовых. Согласно статистическим наблюдениям, если банк одобрит n% (n>0) заявок на кредит, то получит (0,1+0,1n)% проблемных должников (не выплачивающих кредитные платежи). Какой целочисленный процент кредитных заявок следует одобрять ипотечному банку, чтобы максимизировать операционную прибыль, если размер выручки пропорционален проценту одобренных заявок, помноженному на средний процент прибыли банка от всех кредитных договоров? 18. Найдите все значения параметра a, при которых решением неравенства
19. У Пети на счету 500$. Раз в месяц Петя либо кладет на счет 27$, либо снимает 60$. А) Мог ли в какой-то момент времени баланс Пети равняться нулю? Б) Какой минимальный остаток средств мог оказаться на счету Пети? В) За какое минимальное количество транзакций (пополнений и снятий) может быть достигнут этот минимальный остаток?

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


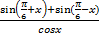
 где
где  — постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж.
— постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж.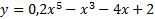
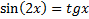 .
.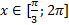
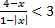
 является отрезок?
является отрезок?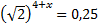

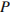 (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле
(в паскалях), оказываемое навесом и колонной на опору, определяется по формуле 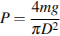 , где
, где  кг – общая масса навеса и колонны,
кг – общая масса навеса и колонны,  – диаметр колонны (в метрах). Считая ускорение свободного падения
– диаметр колонны (в метрах). Считая ускорение свободного падения 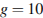 м/с
м/с  , а
, а  , определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400 000 Па. Ответ выразите в метрах.
, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400 000 Па. Ответ выразите в метрах. на отрезке
на отрезке 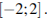
 .
.
 является отрезок?
является отрезок?