Описание метода и установки
Электрическая схема измерительной установки (рис. 13.1) состоит из внешнего сопротивлений 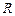 источника постоянного напряжения с электродвижущей силой источника постоянного напряжения с электродвижущей силой 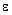 [1] и внутренним сопротивлением [1] и внутренним сопротивлением  . .
В схему включены амперметр и вольтметр, позволяющие измерять ток и падение напряжения во внешней цепи.
 Используя закон Ома для этой замкнутой цепи, можно получить выражение [1] Используя закон Ома для этой замкнутой цепи, можно получить выражение [1]
 , (13.1) , (13.1)
где  – сила тока в цепи; – сила тока в цепи;  – напряжение на сопротивлении – напряжение на сопротивлении 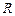 , измеряемое вольтметром (см. рис. 13.1). Следовательно, ожидаемая зависимость напряжения , измеряемое вольтметром (см. рис. 13.1). Следовательно, ожидаемая зависимость напряжения  от силы тока от силы тока  имеет вид имеет вид
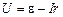 . (13.1¢) . (13.1¢)
График этой зависимости представлен прямой линией а на рис. 13.2. Причем пересечение графика с осью напряжений (  ) проходит в точке ) проходит в точке 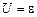 , а точка пересечения графика с осью токов ( , а точка пересечения графика с осью токов (  ) дает значение силы тока короткого замыкания источника ) дает значение силы тока короткого замыкания источника  (подробнее об этом токе смотри ниже). Важно отметить, что последнее утверждение – это идеализация. В реальных источниках ЭДС при токах, близких к (подробнее об этом токе смотри ниже). Важно отметить, что последнее утверждение – это идеализация. В реальных источниках ЭДС при токах, близких к  , линейный характер зависимости напряжения , линейный характер зависимости напряжения  от силы тока от силы тока  нарушается, как это показано линией б на рис. 13.2 [3]. У одних источников это вызвано уменьшением ЭДС при таких токах, у других – увеличением внутреннего сопротивления, а у третьих – одновременным влиянием двух названных причин. нарушается, как это показано линией б на рис. 13.2 [3]. У одних источников это вызвано уменьшением ЭДС при таких токах, у других – увеличением внутреннего сопротивления, а у третьих – одновременным влиянием двух названных причин.
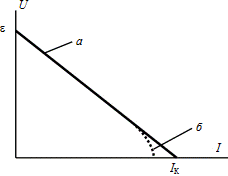
Рис. 13.2
Умножив обе части уравнения (13.1) на силу тока, протекающего по цепи, получим
 . (13.2) . (13.2)
Уравнение (13.2) представим в виде
 , (13.3) , (13.3)
где  – полная мощность, развиваемая источником; – полная мощность, развиваемая источником;  – полезная мощность, т. е. мощность, развиваемая источником во внешней цепи (на сопротивлении R); – полезная мощность, т. е. мощность, развиваемая источником во внешней цепи (на сопротивлении R); 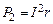 – потери мощности внутри источника (на сопротивлении r). – потери мощности внутри источника (на сопротивлении r).
Установим зависимость этих мощностей от силы тока.
Графически (рис. 13.3) зависимость полной мощности от силы тока  выражается прямой линией, проходящей через начало коор-динат. выражается прямой линией, проходящей через начало коор-динат.

Рис. 13.3
Полезная мощность из (13.2) может быть представлена в виде
 . (13.4) . (13.4)
Эта зависимость выражается параболой. Найдем значение тока, при котором полезная мощность максимальна. Для этого, взяв первую производную 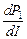 , приравняем ее к нулю , приравняем ее к нулю
 , (13. 5) , (13. 5)
откуда при 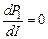 получим получим
 . (13.6) . (13.6)
Так как вторая производная  отрицательна, то при значении силы тока отрицательна, то при значении силы тока  полезная мощность имеет максимум полезная мощность имеет максимум  , величина которого после подстановки (13.6) в (13.4) оказывается равной , величина которого после подстановки (13.6) в (13.4) оказывается равной
 . .
Сравнивая это выражение с ранее полученным  , видим, что при , видим, что при  выполняется равенство выполняется равенство  . Следовательно, полезная мощность . Следовательно, полезная мощность  максимальна при условии, что сопротивление нагрузки равно внутреннему сопротивлению источника питания максимальна при условии, что сопротивление нагрузки равно внутреннему сопротивлению источника питания  . .
Потери мощности определяются зависимостью
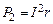 . (13.7) . (13.7)
Графически зависимость P2 от I выражена параболой с вершиной в начале координат и ветвью, направленной вверх (рис. 13.3).
Коэффициентом полезного действия  источника ЭДС называется величина, равная отношению полезной мощности к соответствующей полной мощности источника ЭДС называется величина, равная отношению полезной мощности к соответствующей полной мощности
 . (13.8) . (13.8)
Выражение для U подставим из (13.1¢) в (13.8)
 . (13.9) . (13.9)
Из уравнения (13.9) видно, что зависимость  от от  выражается прямой линией (рис. 13.4), убывающей от значения выражается прямой линией (рис. 13.4), убывающей от значения 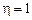 при токе при токе  до значения до значения  при токе при токе
 . (13.10) . (13.10)
Это значение уже упомянутого выше тока короткого замыкания [1]. Действительно, из (13.1) видно, что при внешнем сопротивлении  (короткое замыкание источника) сила тока достигает наибольшего значения, даваемого формулой (13.10). Полезная мощность (короткое замыкание источника) сила тока достигает наибольшего значения, даваемого формулой (13.10). Полезная мощность  при этом убывает до нуля (рис. 13.3), так как при сопротивлении при этом убывает до нуля (рис. 13.3), так как при сопротивлении 
 . .

Рис. 13.4
Полная мощность  и потери мощности и потери мощности 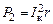 при токе короткого замыкания при токе короткого замыкания  достигают наибольшего значения и равны друг другу достигают наибольшего значения и равны друг другу
 . .
Найдем значение КПД и соотношения между мощностями  , ,  , ,  при максимуме полезной мощности при максимуме полезной мощности  . Так как полезная мощность максимальна при условии, что . Так как полезная мощность максимальна при условии, что  , то КПД при этом равен , то КПД при этом равен
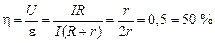 . (13.11) . (13.11)
Отсюда, при токе  ,полезная максимальная мощность равна ,полезная максимальная мощность равна  . Используя (13.3), при токе . Используя (13.3), при токе  получаем равенство полезной мощности и мощности потерь получаем равенство полезной мощности и мощности потерь  . .
Из графиков зависимостей мощностей и КПД от силы тока
(рис. 13.3, 13.4) видим, что условия получения наибольшей полезной мощности  и наибольшего КПД и наибольшего КПД 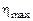 несовместимы. Когда несовместимы. Когда  достигает наибольшего значения, сила тока равна достигает наибольшего значения, сила тока равна  и и  или 50 %. Когда же КПД близок к единице, полезная мощность или 50 %. Когда же КПД близок к единице, полезная мощность  мала по сравнению с максимальной мощностью мала по сравнению с максимальной мощностью  , которую мог бы развить данный источник. , которую мог бы развить данный источник.
Выразив напряжение 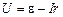 (13.1¢), построим зависимость (13.1¢), построим зависимость 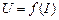 (рис. 13.2). Это – прямая, спадающая от значения (рис. 13.2). Это – прямая, спадающая от значения  (напря-жение холостого хода), равного (напря-жение холостого хода), равного  , до нуля при токе, равном току короткого замыкания. Графический метод определения тока короткого замыкания , до нуля при токе, равном току короткого замыкания. Графический метод определения тока короткого замыкания  и ЭДС и ЭДС  , так называемый метод короткого замыкания и холостого хода позволяет без измерения определить , так называемый метод короткого замыкания и холостого хода позволяет без измерения определить  и и 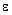 . .
На практике он используется следующим образом. Изменяя в некоторых пределах сопротивление 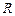 , измеряют несколько значений тока , измеряют несколько значений тока  и соответствующие значения напряжения и соответствующие значения напряжения  . На чертеже строят зависимость . На чертеже строят зависимость 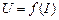 , графиком которой будет прямая линия. Продолжив ее до пересечения с осью напряжения , графиком которой будет прямая линия. Продолжив ее до пересечения с осью напряжения  , находят значение , находят значение  , а до пересечения с осью тока , а до пересечения с осью тока  – ток – ток  . Внутреннее сопротивление источника ЭДС определяют по формуле . Внутреннее сопротивление источника ЭДС определяют по формуле
 . (13.12) . (13.12)
Задание к работе
1. Предварительно подготовьте протокол, в котором начертите таблицу для прямых и косвенных измерений.
2. Постройте на миллиметровой бумаге необходимые оси координат.
3. Соберите электрическую схему установки. В качестве источника с электродвижущей силой 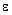 и внутренним сопротивлением и внутренним сопротивлением  используйте генератор постоянного напряжения ГПН с включенным тумблером «Внутреннее сопротивление» используйте генератор постоянного напряжения ГПН с включенным тумблером «Внутреннее сопротивление» 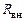 на его передней панели. на его передней панели.
4. Изменяя сопротивление 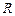 цепи, снимите зависимость цепи, снимите зависимость  от от  и постройте ее график. Определите по графику путем его экстраполяции до пересечения с осями координат значения ЭДС и тока короткого замыкания и постройте ее график. Определите по графику путем его экстраполяции до пересечения с осями координат значения ЭДС и тока короткого замыкания  . .
5. Определите по формуле (13.12) внутреннее сопротивление r источника тока.
6. Вычислите значения  , ,  , ,  , ,  . .
7. Постройте зависимости этих величин от силы тока, экстраполируя кривые и прямые до пересечения с осями координат.
Вопросы к защите
1. Запишите закон Ома для замкнутой цепи. В чем состоит физический смысл ЭДС?
2. Каким нужно сделать сопротивление вольтметра, чтобы измеренное им значение ЭДС было бы как можно ближе к истинному?
3. Дайте определение полной, полезной мощности и мощности потерь.
4. При каком условии полезная мощность будет максимальной? Докажите.
5. Проанализируйте зависимости мощностей P, P1, P2 от силы тока.
6. Что называется коэффициентом полезного действия батареи? Проанализируйте зависимость h = f(I).
7. Сравните полученные опытным путем зависимости с теоретическими.
8. Охарактеризуйте физический смысл напряжения, разности потенциалов.
9. Как определить силу тока короткого замыкания и ЭДС батареи, сняв зависимость напряжения от силы тока?
Список литературы
1. Калашников С.Г. Электричество. – М.: Наука, 1964.
2. Савельев И.В. Курс общей физики. – М.: Наука, 1978. – Т. 2
(и последующие издания этого курса).
3. Зевеке Г.В., Ионкин П.А., Нетушил А.В. и др. Основы теории цепей. – М.: Энергоатомиздат, 1989.
Лабораторная работа № 15
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


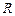 источника постоянного напряжения с электродвижущей силой
источника постоянного напряжения с электродвижущей силой 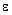 [1] и внутренним сопротивлением
[1] и внутренним сопротивлением  .
.  Используя закон Ома для этой замкнутой цепи, можно получить выражение [1]
Используя закон Ома для этой замкнутой цепи, можно получить выражение [1] , (13.1)
, (13.1) – сила тока в цепи;
– сила тока в цепи;  – напряжение на сопротивлении
– напряжение на сопротивлении  от силы тока
от силы тока 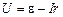 . (13.1¢)
. (13.1¢) ) проходит в точке
) проходит в точке 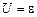 , а точка пересечения графика с осью токов (
, а точка пересечения графика с осью токов (  ) дает значение силы тока короткого замыкания источника
) дает значение силы тока короткого замыкания источника  (подробнее об этом токе смотри ниже). Важно отметить, что последнее утверждение – это идеализация. В реальных источниках ЭДС при токах, близких к
(подробнее об этом токе смотри ниже). Важно отметить, что последнее утверждение – это идеализация. В реальных источниках ЭДС при токах, близких к  , линейный характер зависимости напряжения
, линейный характер зависимости напряжения 
 . (13.2)
. (13.2) , (13.3)
, (13.3) – полная мощность, развиваемая источником;
– полная мощность, развиваемая источником;  – полезная мощность, т. е. мощность, развиваемая источником во внешней цепи (на сопротивлении R);
– полезная мощность, т. е. мощность, развиваемая источником во внешней цепи (на сопротивлении R); 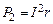 – потери мощности внутри источника (на сопротивлении r).
– потери мощности внутри источника (на сопротивлении r). выражается прямой линией, проходящей через начало коор-динат.
выражается прямой линией, проходящей через начало коор-динат.
 . (13.4)
. (13.4)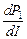 , приравняем ее к нулю
, приравняем ее к нулю , (13. 5)
, (13. 5)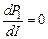 получим
получим . (13.6)
. (13.6) отрицательна, то при значении силы тока
отрицательна, то при значении силы тока  полезная мощность имеет максимум
полезная мощность имеет максимум  , величина которого после подстановки (13.6) в (13.4) оказывается равной
, величина которого после подстановки (13.6) в (13.4) оказывается равной .
. , видим, что при
, видим, что при  выполняется равенство
выполняется равенство  . Следовательно, полезная мощность
. Следовательно, полезная мощность  максимальна при условии, что сопротивление нагрузки равно внутреннему сопротивлению источника питания
максимальна при условии, что сопротивление нагрузки равно внутреннему сопротивлению источника питания  источника ЭДС называется величина, равная отношению полезной мощности к соответствующей полной мощности
источника ЭДС называется величина, равная отношению полезной мощности к соответствующей полной мощности . (13.8)
. (13.8) . (13.9)
. (13.9)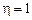 при токе
при токе  при токе
при токе . (13.10)
. (13.10) (короткое замыкание источника) сила тока достигает наибольшего значения, даваемого формулой (13.10). Полезная мощность
(короткое замыкание источника) сила тока достигает наибольшего значения, даваемого формулой (13.10). Полезная мощность  .
.
 и потери мощности
и потери мощности 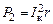 при токе короткого замыкания
при токе короткого замыкания  .
. ,
,  при максимуме полезной мощности
при максимуме полезной мощности  . Так как полезная мощность максимальна при условии, что
. Так как полезная мощность максимальна при условии, что 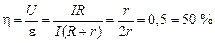 . (13.11)
. (13.11) . Используя (13.3), при токе
. Используя (13.3), при токе  .
.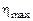 несовместимы. Когда
несовместимы. Когда  или 50 %. Когда же КПД близок к единице, полезная мощность
или 50 %. Когда же КПД близок к единице, полезная мощность 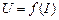 (рис. 13.2). Это – прямая, спадающая от значения
(рис. 13.2). Это – прямая, спадающая от значения  (напря-жение холостого хода), равного
(напря-жение холостого хода), равного  , до нуля при токе, равном току короткого замыкания. Графический метод определения тока короткого замыкания
, до нуля при токе, равном току короткого замыкания. Графический метод определения тока короткого замыкания  , так называемый метод короткого замыкания и холостого хода позволяет без измерения определить
, так называемый метод короткого замыкания и холостого хода позволяет без измерения определить  . (13.12)
. (13.12)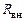 на его передней панели.
на его передней панели.