
|
|
Растет характеристик цикла12 Тепло за цикл
Работа за цикл
Известно, что за цикл
Количество подведенного тепла
Найдем изменения внутренней энергии, энтальпии и энтропии за цикл. Теоретически эти изменения должны быть равными нулю.
Некоторые отличия рассчитанных величин от нулей объясняются округлениями при расчетах. Естественно, что сопоставлять невязки, например, нужно не с нулем, а с любым слагаемым, входящим в сумму. И тогда видно что невязка и здесь составляет доли процента. Рассчитываем термический КПД цикла
Рассчитываем термический КПД идеализированного цикла с адиабатными процессами сжатия и расширения по формуле, приведенной в [1] и принимая в среднем k=1,39:
Термический КПД цикла Карло для того же интервала температур, в котором реализуется реальный цикл
Результаты расчетов заносим в сводную таблицу 1. Таблица 1. Сводная таблица исходных данных и результатов расчета.
Построение T-s диаграммы цикла Чтобы построить T-s диаграмму, выбираем масштабы по осям координат:T=10 К/мм, s=0,01 кДж/(кг×К)/мм. Изображаем оси T и s, наносим координатную сетку, а затем и характерные точки цикла. Точки 2 и 3, 3 и 4, 5 и 1 соединяем по лекалу кривыми, по характеру близкими к экспонентам, а политропные процессы 1-2 и 4-5 с достаточной точностью можно изображать прямыми линиями (см. рис. 2). Чтобы определить коэффициент заполнения цикла, найдем площадь цикла 1-2-3-4-5-1 непосредственно на диаграмме, пересчитывая квадратные сантиметры (на рисунке пронумерованы): Fц= =25,4 см2. Площадь описанного цикла Карно рассчитываем, измерив, размеры прямоугольника в сантиметрах: Fк=8,5×5,9=50,2 см2. Тогда коэффициент заполнения цикла будет
Рис.2. Т-s диаграмма цикла
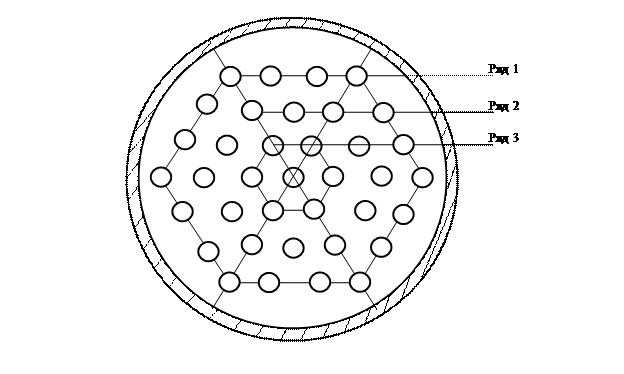
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ b2[†]. Задача b2-15.Определить поверхность теплообмена кожухотруб-чатого конденсатора, предназначенного для конденсации сухого насыщенного водяного пара при давлении p1 = 0,15, МПа в количестве М1 = 4600 кг/ч. Охлаждение осуществляется водой, протекающей внутри латунных трубок с размерами Ø 19x1 мм. Средняя скорость воды в трубках w2 = 1,6 м/с. Начальная температура воды t21 = 18 °С. Трубки в количестве Z= 91 шт. размещены в цилиндрическом корпусе и расположены по сторонам и вершинам правильных шестиугольников. Положение аппарата горизонтальное. Представим сначала общую схему теплообменника (рис. 3) и схему расположения трубок внутри его корпуса (рис. 4).
Рис. 3. Общая схема конденсатора
Рис. 4. Расположение греющих трубок
Поверхность теплообмена F найдем из основного уравнения теплопередачи:
где Q – передаваемый тепловой поток, Вт; k – средний температурный напор между теплоносителями. Определив F, найдем затем и необходимую длину трубок L. Из формулы (10) видно: чтобы найти F, необходимо предварительно рассчитать значения Q , k и Dtср . Будем считать, что образующийся в аппарате конденсат не переохлаждается. В этом случае можем определить тепловую нагрузку Q по заданному расходу пара М1 и его теплоте парообразования r.
Пересчитаем сначала М1 в систему СИ: М1 = 4600 / 3600 = 1,28 кг/с. Значение r будем определять линейным интерполированием по таблице свойств насыщенного пара [4, с. 265, табл. 12]. Для этого подробнее рассмотрим процедуру линейного интерполирования. На рис. 5 графически (точками 1 и 2) отражена некая табличная зависимость Y = f(X). Постулируя линейную зависимость между Y и X на интервале Х1 - Х2, проводим через эти точки прямую линию и для некоторого промежуточного значения X из подобия треугольников 12С и 1АВ запишем соотношения между отрезками:
откуда находим
Рис. 5. Линейное интерполирование
Отметим, что полученная формула может применяться и для убывающих зависимостей, и для экстрополирования данных. Она удобна еще и тем, что множитель (Х-Х1) / (Х2-Х1) остается одинаковым для любых параметров, зависящих от X. Итак, используя таблицу свойств насыщенного пара, по формуле (12) рассчитываем
Далее по формуле (11) рассчитываем Q = 1,28 · 2226,5 ·103 = 2849,9 · 103 Вт. Если пренебрегать тепловыми потерями в окружающую среду, то этот же тепловой поток воспринимается и охлаждающей водой, и для нее можно записать
где М2 - массовый расход воды; ср2 - удельная теплоемкость воды; t22 и t21 - температуры воды на входе и выходе из теплообменника. Расход воды М2 находим по уравнению неразрывности [2]:
где f2 - общая площадь поперечного сечения для потока воды; ρ2 - плотность воды при ее средней температуре Чтобы по таблице свойств воды [4, с. 264, табл. 11] найти ее плотность и теплоемкость, зададимся в первом приближении температурой t22 приняв t22 = 52 °С. Тогда
Линейным интерполированием находим r2 = 993,9 кг/м3, ср1 = 4,174 кДж/кг. Рассчитываем величину f2, учитывая, что внутренний диаметр трубки меньше наружного диаметра на две толщины (dвн = dнap - 2δ = 19 - 2·1 = 17 мм):
Тогда расход охлаждающей воды будет
Из уравнения (13) получаем формулу для t22 и рассчитываем эту величину:
Отметим, что хотя величина t22 получилась и не очень близкой к принятой в первом приближении, дальнейших уточнений ее не требуется, поскольку значения ср2 и ρ2 при изменении температуры изменяются весьма незначительно. Действительно, во втором приближении t2cр=(t22 + t21)/2 =(38,8+18)/2 = =28,4 °С, а при этой температуре ρ2 = 996,1 (найдено интерполированием) и это значение менее чем на 0,2 % отличается от полученного при первом приближении. Так что для дальнейших расчетов принимаем t22 = 38,8 °С, t2ср = 28,4 °С. Определяем средний температурный напор Dtср, изобразив условную схему движения теплоносителей (рис. 6) и определив значения напоров на входе и выходе из аппарата. Обычно Dtср определяется как среднелогарифмический напор:
но у нас Dtб / Dtм = 93,3 / 72,5 = 1,29, что меньше 2, и, следовательно, можно рассчитывать среднеарифметический напор:
Чтобы убедиться в этом, рассчитаем все же и среднелогарифмический температурный напор:
что практически совпадает с предыдущим результатом.
Поскольку у нас dн / dвн= 19 / 17 = 1,12 (меньше 2), то значение коэффициента теплопередачи k можно рассчитать по формуле для плоской стенки:
где a1 и a2 - коэффициенты теплоотдачи от горячего теплоносителя (от конденсирующегося пара) к наружной стенке трубки и к холодному теплоносителю (от внутренней стенки к воде); dст и dнак - толщина стенки и слоя накипи; lст и lнак - коэффициенты теплопроводности материала трубки и накипи, соответственно. Заметим, что в нашем задании lнак = 0 и формула (14) несколько упрощается. Чтобы реализовать формулу (14), нужно рассчитать предварительно значения a1 и a2. Коэффициент теплоотдачи при конденсации насыщенного пара на горизонтальных пучках рассчитывают по формуле Нуссельта для одиночной горизонтальной трубы с введением специального поправочного множителя εп зависящего от числа труб п в одном вертикальном ряду [2]:
В формулу входят неизвестное значение температуры стенки со стороны конденсата tc1 (аналогичная ситуация возникает и при расчетах a2, только там неизвестная будет tс2), а также теплофизические характеристики r1, λ1 и μ1 конденсата. Поэтому задачу решаем методом последовательных приближений, рассчитывая в соответствии с рекомендациями [2] первые приближения tc1 и tc2 так:
Линейным интерполированием по формуле (12) находим значения r1 и λ1 воды при заданном давлении насыщенного пара рн = 0,15 МПа, используя табличные данные [4, с. 264, табл. 11]: r1 =951,0 + 0,1273·(943,1 - 951,0) = 950 кг/м3 λ1 = 0,685 + 0,1273 ·(0,686 - 0,685) = 0,685 Вт/(м·К). Линейное интерполирование вязкости может приводить к недопустимо большим погрешностям, поэтому рекомендуется использовать температурную корреляцию Андраде и значение μ1 рассчитывать по формуле [6]:
где m1t и m2t - табличные значения m, соответствующие табличным температурам t1 и t2; t - температура, при которой нужно определить значение m. Пользуясь данными из [4, с. 237, табл. 4], рассчитываем:
Величину поправочного множителя εп находим как для шахматного пучка, определив предварительно по схеме (рис. 4) число труб, расположенных в одном вертикальном ряду: п = 6. Тогда, используя формулу из [2], рассчитываем
Теперь рассчитываем α1п по формуле (15):
Чтобы рассчитать коэффициент теплоотдачи от стенки к холодному теплоносителю (теплоотдача при движении теплоносителя в трубе), сначала установим режим течения теплоносителя, рассчитав значение критерия Re [2]:
где v2 - коэффициент кинематической вязкости воды при ее средней температуре t2ср = 28,4 °С. Рассчитываем эту величину, используя данные пособия [4, табл. 4] и применяя формулу (16):
Тогда по формуле (17)
Поскольку Re > 104, то режим течения воды турбулентный, и для него рекомендуется критериальное уравнение М.А. Михеева:
где Рrж2 и Рrс2 - значения критерия Прандтля при температурах tж2 и tс2, соответственно; εl - поправочный множитель, учитывающий влияние начального участка трубы. Для труб, длина которых более двадцати диаметров, εl = 1. Значения Ргж2 и Ргс2 находим интерполированием по формуле (16):
Определяем значение числа Нуссельта по формуле (18):
после чего находим значение коэффициента теплоотдачи [2]
где λ2 находим линейным интерполированием по формуле (12):
Рассчитываем α2 по формуле (19):
Рассчитываем теперь значение коэффициента теплопередачи k в первом приближении, определив предварительно по [4, с. 235, табл. 2] значение коэффициента теплопроводности для меди при tс.ср = 59,9 0С: λст = 394 Вт/(м · К). Тогда по формуле (14) находим
При таком значении k удельный тепловой поток
Именно с этими величинами теперь следует определить во втором приближении значения α1, α2, k и q, a далее tc1 и tс2 в третьем приближении и уж потом сравнить полученные результаты. Если они отличаются от результатов предыдущего приближения менее чем на 5 %, то приближения можно прекратить и рассчитать необходимую поверхность теплообмена по формуле
и далее длину трубок
Все остальные приближения, начиная третьего, выполняются аналогично, но их дальнейший расчет нами не проводится. Приводим результаты расчетов в форме сводной таблицы (табл. 2). 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
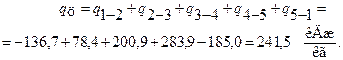
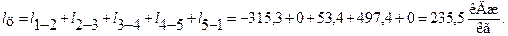
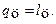 В наших расчетах несовпадение незначительно. Невязка объясняется округлениями в промежуточных расчетах.
В наших расчетах несовпадение незначительно. Невязка объясняется округлениями в промежуточных расчетах.
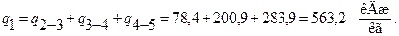
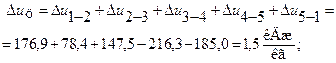

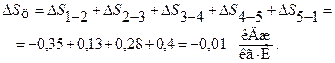
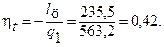

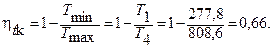
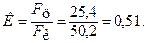





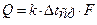 (10)
(10)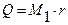 (11)
(11)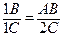 или
или 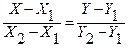
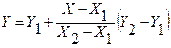 (12)
(12)
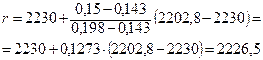 кДж/кг;
кДж/кг;
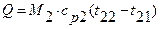 (13)
(13)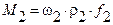 (14)
(14) .
.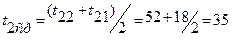 °С
°С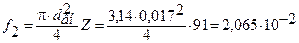 , м2
, м2 , кг/с.
, кг/с. , °С
, °С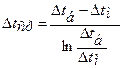
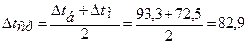 °С.
°С.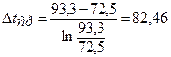 °С.
°С.
 (14)
(14)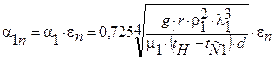 (15)
(15)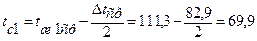 °С,
°С, °С.
°С.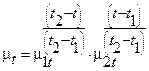 (16)
(16) Н·с/м2
Н·с/м2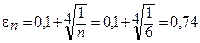
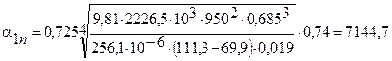 Вт/(м2·К).
Вт/(м2·К).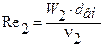 (17)
(17)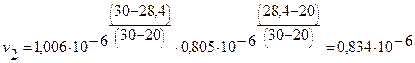 м2/с.
м2/с.
 (18)
(18)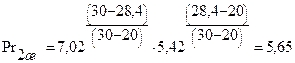
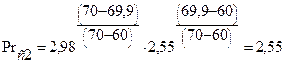

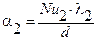 (19)
(19)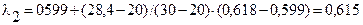 Вт/(м·К).
Вт/(м·К). Вт/(м2·К).
Вт/(м2·К).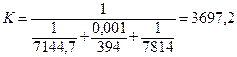 Вт/(м2·К).
Вт/(м2·К).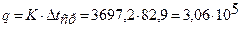 Вт/м2.
Вт/м2. Рассчитаем теперь значения tс1 и tc2 во втором приближении [2]:
Рассчитаем теперь значения tс1 и tc2 во втором приближении [2]: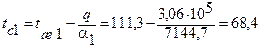 °С,
°С,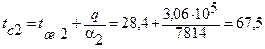 °С.
°С.
