
|
|
Первое начало термодинамики12 С помощью первого закона термодинамики можно делать важные заключения о характере протекающих процессов. Наиболее просто выглядят изопроцессы в идеальном газе. а) Если
т.е. изменение внутренней энергии системы равно количеству переданной системе теплоты. б) Изотермический процесс. Поскольку в) При изобарном процессе передаваемое системе количество теплоты идет на изменение внутренней энергии и совершение работы (при постоянном давлении). Поэтому теплоемкость газа при постоянном давлении больше, чем при постоянном объеме. г) Процесс в теплоизолированной системе называется адиабатным. Он тоже представляет собой изопроцесс, но функция состояния, сохраняющаяся в этом процессе (энтропия) не изучается в курсе физики средней школы. При адиабатном процессе
Конечно, последнее выражение можно представить и в виде т.е. при адиабатном процессе работа совершается за счет убыли внутренней энергии системы. Уравнение Пуассона для адиабатического процесса:
Связь параметров газа при адиабатическом процессе: Тепловые машины Если
Коэффициентом полезного действия (КПД) тепловой машины называется отношение
Теоретически наивысшим для заданных Т1 (максимальной температуре в цикле) и Т2 (минимальной температуре в цикле) является КПД идеального цикла Карно, равный
где Т1 – температура нагревателя (от которого рабочее тело получает тепло Q1) и Т2 – температура холодильника (которому рабочее тело передает тепло Q2).
Примеры решения задач Задача 1 В сосуд с теплоемкостью
Дано:
Найти:
Решение: Здесь четыре тела участвуют в теплообмене и много тепловых процессов с ними происходит, но, по крайней мере из условия задачи ясно, что в конце концов произойдёт: лёд растает и образовавшаяся из него вода вместе с водой, в которой плавал лёд, и сосудом нагреются до температуры тёплового равновесия Рассмотрим, какие тела получают теплоту, и в каких процессах они при этом участвуют: а) получает теплоту сосуд, который при этом нагревается от б) получает тепло вода, в которой лёд плавал до впуска пара. Она тоже нагревается от в) получает тепло лёд, плававший в воде и поэтому имевший температуру Затем вода, образовавшаяся из растаявшего льда, станет нагреваться от
Больше нет никаких тел, получающих тепло, и никаких процессов, сопровождающихся получением теплоты. Телом, которое отдаёт тепло, является пар. Если бы он был стоградусным, то сразу стал бы конденсироваться, но так как его температура Затем пар будет конденсироваться при
По закону сохранения энергии сумма всех полученных сосудом, льдом и водой количеств теплоты
или
Мы записали уравнение теплового баланса для этой задачи. Из него, выполнив необходимые преобразования, мы найдём искомую температуру теплового равновесия
Рисунок Б.1
Мы решили задачу в общем виде. На рисунке Б.1 показан график функции Ответ:

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (изохорный процесс), то работа газом не производится, и можно записать
(изохорный процесс), то работа газом не производится, и можно записать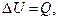 (А.9)
(А.9) , то внутренняя энергия идеального газа не меняется. Тогда все переданное системе количество теплоты идет на совершение работы системой
, то внутренняя энергия идеального газа не меняется. Тогда все переданное системе количество теплоты идет на совершение работы системой  (А.10)
(А.10)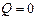 , изменение внутренней энергии происходит только за счет совершения работы.
, изменение внутренней энергии происходит только за счет совершения работы. (А.11)
(А.11) (А.12)
(А.12)

 и
и  - абсолютные величины количеств теплоты, полученного машиной (рабочим телом машины) от нагревателя и переданного холодильнику за цикл, соответственно, то для работы, производимой машиной за цикл, справедливо выражение
- абсолютные величины количеств теплоты, полученного машиной (рабочим телом машины) от нагревателя и переданного холодильнику за цикл, соответственно, то для работы, производимой машиной за цикл, справедливо выражение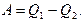 (А.13)
(А.13) (А.14)
(А.14) (А.15)
(А.15) ПРИЛОЖЕНИЕ Б
ПРИЛОЖЕНИЕ Б , налита вода массой
, налита вода массой  , в которой плавает лед массой
, в которой плавает лед массой  . В сосуд впускают пар массой
. В сосуд впускают пар массой  при температуре
при температуре 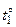 выше
выше  . Какая температура
. Какая температура  установится в сосуде при тепловом равновесии, если известно, что весь лед растаял, а пар сконденсировался? Удельная теплоемкость воды
установится в сосуде при тепловом равновесии, если известно, что весь лед растаял, а пар сконденсировался? Удельная теплоемкость воды 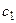 , удельная теплоемкость пара
, удельная теплоемкость пара  , удельная теплота плавления льда
, удельная теплота плавления льда  ,удельная теплота парообразования воды
,удельная теплота парообразования воды  .
.  , где
, где  и
и  .
.
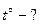
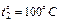 , сконденсируется при
, сконденсируется при  , а затем вода, образовавшаяся из пара, охладится до температуры
, а затем вода, образовавшаяся из пара, охладится до температуры  ;
; до
до  ;
; . При этом лёд вначале тает. Количество теплоты, которое лёд получает в процессе таяния:
. При этом лёд вначале тает. Количество теплоты, которое лёд получает в процессе таяния: 
 .
. .
. .
. После этого вода, образовавшаяся из пара и имеющая при этом температуру
После этого вода, образовавшаяся из пара и имеющая при этом температуру  .
. и
и  равна сумме всех отданных количеств теплоты
равна сумме всех отданных количеств теплоты  и
и 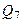 :
:
 .
.



 .
. Приложение В
Приложение В