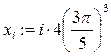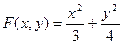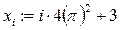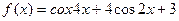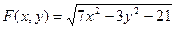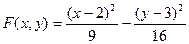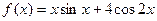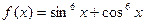|
|
Теоретическое обоснованиеОсновы программирования и графические возможности системы MATLAB Цель и содержание работы:познакомиться с элементами программирования и возможностями графической визуализации вычислений в пакете MATLAB.
Теоретическое обоснование Программирование в системе MATLAB является эффективным средством ее расширения и адаптации к решению специфических проблем. Оно реализуется с помощью языка программирования системы. Большинство объектов этого языка, в частности все команды, операторы и функции, одновременно являются объектами входного языка общения с системой в командном режиме работы. С позиций программиста язык программирования системы является типичным проблемно-ориентированным языком программирования высокого уровня. Точнее говоря, это даже язык сверхвысокого уровня, содержащий сложные операторы и функции, реализация которых на обычных языках (например, Бейсике, Паскале или Си) потребовала бы много усилий и времени. К таким функциям относятся матричные функции, функции быстрого преобразования Фурье и др., а к операторам — операторы построения разнообразных графиков, генерации матриц определенного вида и т. д. Программами в системе MATLAB являются М-файлы текстового формата, содержащие запись программ в виде программных кодов. Язык программирования системы MATLAB имеет следующие средства: · данные различного типа; · константы и переменные; · операторы, включая операторы математических выражений; · встроенные команды и функции; · функции пользователя; · управляющие структуры; · системные операторы и функции; · средства расширения языка. Коды программ в системе MATLAB пишутся на языке высокого уровня, достаточно понятном для пользователей умеренной квалификации в области программирования. Язык программирования MATLAB является типичным интерпретатором. Это означает, что каждая инструкция программы распознается и тут же исполняется, что облегчает обеспечение диалогового режима общения с системой. Язык программирования системы MATLAB вобрал в себя все средства, необходимые для реализации различных видов программирования: · процедурного; · операторного; · функционального; · логического; · структурного (модульного); · объектно-ориентированного; · визуально-ориентированного. В основе процедурного, операторного и функционального типов программирования лежат процедуры, операторы и функции, используемые как основные объекты языка. Эти типы объектов присутствуют в MATLAB. Логическое программирование реализуется в MATLAB с помощью логических операторов и функций. Это позволяет реализовать основные идеи логического программирования, хотя на выдающуюся роль в этом классе языков программирования MATLAB не претендует. Зато MATLAB представляет собой яркий пример плодотворности структурного программирования. Подавляющее большинство функций и команд языка представляют собой вполне законченные модули, обмен данными между которыми происходит через их входные параметры, хотя возможен обмен информацией и через глобальные переменные. Программные модули оформлены в виде текстовых М-файлов, которые хранятся на диске и подключаются к программам по мере необходимости. Важно отметить, что в отличие от многих языков программирования, применение тех или иных модулей не требует предварительного объявления, а для создания и отладки самостоятельных модулей MATLAB имеет все необходимые средства. Подавляющее большинство команд и функций системы MATLAB поставляется в виде таких модулей. Объектно-ориентированное программирование также широко представлено в системе MATLAB. Оно особенно актуально при программировании задач графики. Что качается визуально-ориентированного программирования, то в MATLAB оно представлено в основном в пакете моделирования заданных блоками устройств и систем Simulink. В ядре системы в данный момент визуально-ориентированное программирование не используется. В MATLAB реализованы возможности по организации циклов и использованию условных операторов. Условный оператор if в общем виде записывается следующим образом: if Условие Инструкции_1 else Инструкции_2 end
Пока Условие возвращает логическое значение 1 (то есть «истина»), выполняются Инструкции_1, в противном случае выполняются Инструкции_2. Инструкции в списке разделяются оператором , (запятая) или ; (точка с запятой). При этом оператор end указывает на конец перечня инструкций. Условия записываются в виде: Выражение_1 Оператор_отношения Выражение_2, причем в качестве Операторов_отношения используются следующие операторы: ==, <, >, <=, >= или ~=. Все эти операторы представляют собой пары символов без пробелов между ними. Допускается также такой вариант условного оператора: if Условие Инструкции_1 elself Условие Инструкции_2 else Инструкции_3 end Циклы типа for...end обычно используются для организации вычислений с заданным числом повторений. Конструкция такого цикла имеет следующий вид: for vаг=Выражение. Инструкция_1 . . Инструкция_N end Выражение чаще всего записывается в виде s:d:e, где s — начальное значение переменной цикла var, d — приращение этой переменной и е — конечное значение управляющей переменной, при достижении которого цикл завершается. Возможна и запись в виде s :е (в этом случае d=l). Список выполняемых в цикле инструкций завершается оператором end. Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса. Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов. В режиме непосредственных вычислений доступны практически все возможности системы. Широко используется, например, построение графиков различных функций, дающих наглядное представление об их поведении в широком диапазоне изменения аргумента. При этом графики строятся в отдельных масштабируемых и перемещаемых окнах. MATLAB строит графики функций по ряду точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале между смежными точками. Графики MATLAB строит в отдельных окнах Figure, называемых графическими окнами. В главном меню окна появилась позиция Tools (Инструменты), которая позволяет вывести или скрыть инструментальную панель, видимую в верхней части окна графики на рис. 1. Средства этой панели позволяют легко управлять параметрами графиков и наносить на них текстовые комментарии в любом месте.
Рисунок – 1 Пример построения графика синусоиды
Графики в MATLAB можно строить как в командном режиме из Окна команд, так и вызывая их из М-файлов. Для построения двумерных графиков используется команда plot. В общем случае синтаксис команды plot выглядит следующим образом: plot(x, y, ’цвет_стиль_маркер‘), где x – аргумент функции; y – значение функции; цвет и стиль линий графика, также маркер определены в таблице 1. Таблица 1 – Цвет, тип линии и тип точки на графике
Вызов функции plot с многочисленными парами x и y создает многочисленные графики. При этом MATLAB автоматически присваивает каждому графику свой цвет (исключая случаи, когда это делает сам пользователь), что позволяет различать заданные наборы данных. Например plot(t, f, ‘r-*’, t, y ‘b--+’, t, s, ‘g-.o’) – в этом случае на одной координатной плоскости будут выведены графики трех функций: f(t) – красный с маркером *; y(t) – синий с маркером +; s(t) – зеленый с маркером о. При этом стиль линий также будет различным. Если не указывать параметры ‘цвет_стиль_маркер’, то цвет будет присвоен автоматически, линия будет сплошной, а маркер отсутствовать. Функции xlabel, ylable, zlable добавляют подписи к соответствующим осям, функция title добавляет заголовок в верхнюю часть окна , а функция text вставляет текст в любое место графика. Трехмерные поверхности обычно описываются функцией двух переменных z(x, у). Специфика построения трехмерных графиков требует не просто задания ряда значений х и у, то есть векторов х и у. Она требует определения для X и Y двумерных массивов — матриц. Для создания таких массивов служит функция meshgrid. В основном она используется совместно с функциями построения графиков трехмерных поверхностей. Функция meshgrid создает матрицы Х и Y, состоящие из повторяющихся строк и столбцов соответственно. Строки матрицы Х дублируют вектор х, а столбцы Y – вектор y. Синтаксис функции meshgrid: [X,Y] = meshgrid(x,y) Для построения графиков поверхностей используются функции mesh и surface. MATLAB определяет поверхность как z координаты точек над координатной сеткой плоскости x – y, используя прямые линии для соединения соседних точек. Функции mesh и surface отображают поверхность в трех измерениях. При этом mesh создает каркасную поверхность, где цветные линии соединяют только заданные точки, а функция surface вместе с линиями отображает в цвете и саму поверхность. Для установки палитры цветов трехмерных графиков служит команда colormap, записываемая в следующей форме сolormap цвет, где параметр «цвет» может принимать следующие значения · hsv — цвета радуги; · hot — чередование черного, красного, желтого и белого цветов; · gray — линейная палитра в оттенках серого цвета; · bone — серые цвета с оттенком синего; · copper — линейная палитра с оттенками меди; · pink — розовые цвета с оттенками пастели; · white — палитра белого цвета; · flag — чередование красного, белого, синего и черного цветов; · lines — палитра с чередованием цветов линий; · colorcube — расширенная палитра RGB; · jet — разновидность палитры HSV; · prism — призматическая палитра цветов; · cool — оттенки голубого и фиолетового цветов; · autumn — оттенки красного и желтого цветов; · spring — оттенки желтого и фиолетового цветов; · winter — оттенки синего и зеленого цветов; · summer — оттенки зеленого и желтого цветов. Уже построенные графики удобно редактировать в графическом окне Figure. Для этого используется панель инструментов, с помощью которой можно менять толщину, цвет, маркер линий. Также на панели инструментов есть «графическая лупа» («+» « – » ), позволяющая увеличивать и уменьшать отдельные части графика. В одном графическом окне можно одновременно вывести несколько графиков. Для этого графическое окно разбивается на необходимое количество окон командой subplot(m,n,p) или subplot(m n p) Эта команда разбивает графическое окно на тхп подокон, при этом m — число подокон по горизонтали, n — число подокон по вертикали, а р— номер подокна, в которое будет выводиться текущий график (подокна отсчитываются последовательно по строкам). Например » х=-5:0.1:5; subplot(1.2.1), plot(x.sin(x)) subplot(1.2.2), plot(sin(5*x).cos(2*x+0.2)) При этом графическое окно разобьется на два подокна в первом будет выведен график функции sin(x), во втором – зависимость cos(2x+0,2) от sin(5x). Задание 1. Создать файл-сценарий с программой для решения следующей задачи. Для восьми различных наборов значений коэффициентов: а= [-1 2 5 8 10 -4 -11 12], b= [2 -4 12 9 -11 -3 6 10] и с= [4 2 3 -2 -4 7 11 2] найти корни квадратного уравнения 2. Построить график функции одной переменной y=sin(x). Построить несколько графиков, sin(x) и cos(x). в одной координатной плоскости. 3. Построить графики зависимости массивов Х1 и Х2 от номера набора коэффициентов квадратного уравнения. Отредактировать графики. 4. Построить графики функций двух переменных:
Методика выполнения задания. Основы программирования
Блок-схема алгоритма решения квадратного уравнения выглядит так, как показано на рис.2 Этот алгоритм будет реализован в виде файла-функции. Для этого запустите MATLAB. На панели инструментов нажмите иконку Новый М-файл. Открывается окно М-файла. Сюда введите операторы, соответствующие решению квадратного уравнения. Назовем функцию korn. Входными аргументами являются коэффициенты a, b, и с, а выходными – корни уравнения х1 и х2. Функция имеет вид: function [x1,x2]=korn(a,b,c) %Решение квадратного уравнения D=b^2-4*a*c if D>=0 x1=-b+sqrt(D) x2=-b-sqrt(D) else x=’Действительных корней нет’ end
2. Сохраните файл-функцию под именем korn в папке work каталога MATLAB . Для этого нажмите в строке меню Файл – Сохранить как, либо на Панели инструментов нажмите иконку Сохранить. Появляется окно Сохранить как с содержимым папки work (рис.3).
Рисунок 3 – Сохранения М-файла
3. Создайте файл-сценарий для решения задачи формирования массивов X1 и X2 из корней квадратных уравнений при различных значениях коэффициентов. Блок-схема алгоритма решения этой задачи представлена на рис. 4. Предопределенный процесс в этом алгоритме соответствует алгоритму на рис.2.
Аналогично пункту 1 создайте новый М-файл. Запишите программный код, соответствующий представленному алгоритму: %Ввод массивов коэффициентов A=[-1 2 5 8 10 -4 -11 12] B=[2 -4 12 9 -11 -3 6 10] C=[4 2 3 -2 -4 7 11 2] %Формирование массивов корней уравнений for i=1:8 [X1(i),X2(i)]=korn(A(i),B(i),C(i)) Еnd
4. Запустите на выполнение файл-сценарий. Для этого в строке меню выберите Отладка (Debug) – Сохранить и запустить (Save and Run). Появляется окно сохранения М-файла. Назовите файл (например LAB2) и нажмите Сохранить. Происходит выполнения программы. Результаты отображаются в основном окне MATLAB. В Рабочей области окна MATLAB отображаются переменные и массивы, введенные в программу и рассчитанные в ней: массивы коэффициентов А, В, С, массивы результатов Х1 и Х2, а также счетчик циклов i (его последнее значение). Щелкнув дважды левой кнопкой мыши по любому массиву или переменной из Рабочей области, можно раскрыть их значения в специальном окне Array Editor: (рис. 5).
Рисунок 5 – Результаты решения задачи Построение графиков 5. Построим график синусоиды в командном режиме. Очистите Окно команд и Рабочую область от результатов предыдущих вычислений. Для этого в Окне команд введите команду clc, а в Рабочей области вызовите правой кнопкой контекстное меню и выберите Очистить Рабочую область. Теперь зададим интервал изменения аргумента х от 0 до 10с шагом 0.1. Для построения графика достаточно вначале задать вектор х=0:0.1:10, а затем использовать команду построения графиков plot(sin(x)). Результат показан на рис. 1. Вектор х задает интервал изменения независимой переменной от 0 до 10 с шагом 0.1. Почему взят такой шаг, а не, скажем, 1? Дело в том, что plot строит не истинный график функции sin(x), а лишь заданное числом элементов вектора х число точек. Эти точки затем просто соединяются отрезками прямых, т. е. осуществляется кусочно-линейная интерполяция данных графика. При 100 точках полученная кривая глазом воспринимается как вполне плавная, но при 10-20 точках она будет выглядеть состоящей из отрезков прямых. 6. Добавим на график линии сетки. Линии сетки на график добавляются командой >> grid on. Вид графика изменится (рис.6).
Рисунок 6 – Добавление линий сетки на график 7. На одной координатной плоскости можно построить графики нескольких функций. Добавим к построенному графику функции sin(x). График функции cos(x). График sin(x) сделаем красным с точками в виде шестиугольников, cos(x) – зеленым с ромбами. Введем команды: >> plot(x,y1,x,y2) >> y1=sin(x); >> y2=cos(x); >> plot(x,y1,’r-H‘,x,y2,’g-D‘) >> grid on Результат представлен на рис. 7. Рисунок 7 – Два графика на одной координатной плоскости
8. Команды на построение графиков используются в программном коде MATLAB при создании М-файлов. Построите графики зависимости корней квадратного уравнения (Х1 и Х2), от номера набора коэффициентов уравнения. Для этого откройте файл-сценарий LAB2. Добавьте внутри цикла команду t(i)=i Этой командой формируется массив t=[1 2 3 4 5 6 7 8], номеров наборов коэффициентов уравнения ( а. b. c). После цикла введите команды на построение графиков. Программный код М-файла примет следующий вид: %Ввод массивов коэффициентов A=[-1 2 5 8 10 -4 -11 12] B=[2 -4 12 9 -11 -3 6 10] C=[4 2 3 -2 -4 7 11 2] %Формирование массивов корней уравнений for i=1:8 [X1(i),X2(i)]=korn(A(i),B(i),C(i)); t(i)=i; end %Построение графиков plot(t,X1,'r-*',t,X2,'b-o') grid on %Добавление подписей к осям xlabel('номер набора коэффициентов') ylabel('X1 и X2') %Добавление заголовка title('Зависмость Х1 и Х2 от номера набора коэффициентов')
9. Запустите файл на выполнение. Происходит решение задачи и появляется окно графика (рис. 8). Теперь отредактируйте график для большей наглядности. Нажмите на панеле инструментов иконку Редактировать график («1» на рис. 8). Выделите верхний график, вызовите правой кнопкой контекстное меню, выберите Ширина линии – 2.
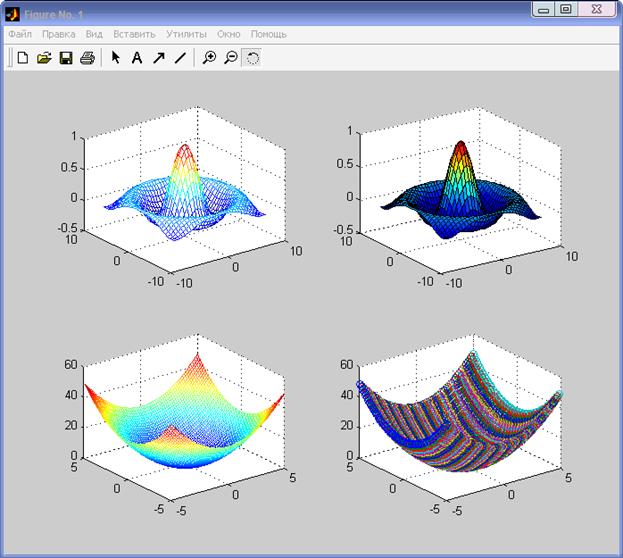
Рисунок 8 – Графики зависимости Х1 и Х2 от номера набора коэффициентов t Добавьте на график надписи и стрелки. Для добавления надписи нажмите иконку А на панели инструментов («2» на рис.8). Теперь вставьте Х1 над красным графиком. Теперь нажмите иконку Вставить стрелку («3» на рис.8) и, зажав левую кнопку мыши, пронтяните стрелку от надписи Х1 к линии графика. Надписи и стрелки можно перетпскивать и поворачивать. Аналогично отредактируйте второй график. 10. Ознакомимся с методикой построения трехмерных графиков функций %Построение графиков поверхности %Создание матриц для построения графиков [X,Y]=meshgrid(-8:0.5:8) [A,B]=meshgrid(-5:0.15:5) %Расчет функции Z R=sqrt(X.^2+Y.^2)+eps Z=sin(R)./R %Расчет функции С C=A.^2+B.^2 %Построение графиков поверхностей в 4-х подокнах грфического окна subplot(2,2,1), mesh(X,Y,Z) subplot(2,2,2), surface(X,Y,Z) grid on subplot(2,2,3), mesh(A,B,C) subplot(2,2,4), plot3(A,B,C,'o') colormap jet grid on
Обратите внимание, что при расчете функций используются операции поэлементного возведения в степень и деления. Функция plot3 обеспечивает построения, аналогичные рассмотренным ранее, но со спецификацией стиля линий и точек, соответствующей спецификации команды plot. Графики функций z и с построены с использованием различных функций. 11. Запустите файл на решение, назвав его Graf3D. В результате появляется графическое окно (рис.9).
Рисунок 9 – Графики функций z(x,y) и c(a,b)
12. Отредактируйте графики, аналогично тому, как описано в пункте 9. Для более наглядного отображения графиков используйте функцию вращения графиков. Для этого на панели инструментов нажмите иконку Вращать трехмерно (рис. 9), наведите курсор на интересующий график и, зажав левую кнопку мыши, вращайте график по своему усмотрению.
Задания для самостоятельной работы Задание 1. Создайте M-файл, где рассчитайте значение функции f(xi) с дискретным аргументом, при i= 1…30. Постройте график этой функции. Задание 2. Постройте график поверхности F(x,y).
Содержание отчёта и его форма В отчёте указывается номер лабораторной работы, её название, цель, перечень изученных в данной работе возможностей MATLAB. Контрольные вопросы и защита работа 1. Продемонстрировать электронный результат выполнения заданий. 2. Знать ответы на вопросы: · Как в MATLAB организовывается цикл с заданным числом повторений? · Какова конструкция условного оператора в MATLAB? · Чем отличаются операторы * и .*? · Какая функция используется для построения двумерных графиков? · Какие функции используется для построения графиков поверхности? 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 . Из найденных корней сформировать два массива X1 и X2.
. Из найденных корней сформировать два массива X1 и X2. , где x и y изменяются от -8 до 8 с шагом 0,5;
, где x и y изменяются от -8 до 8 с шагом 0,5; , где a и b изменяются от -5 до 5 с шагом 0,15
, где a и b изменяются от -5 до 5 с шагом 0,15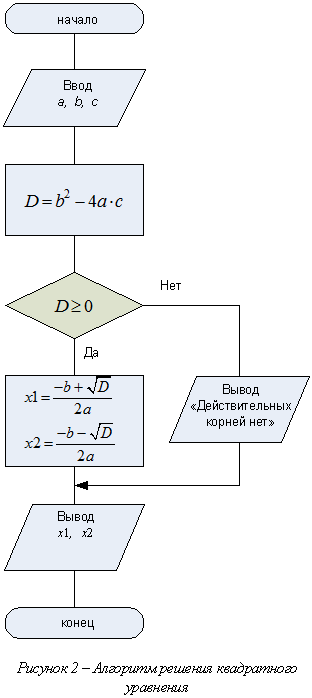 1. Для решения задачи поиска корней квадратных уравнений создадим два М-файла – файл-функцию для решения квадратного уравнения и файл-сценарий для создания массива корней уравнений при различных значениях коэффициентов a, b и с.
1. Для решения задачи поиска корней квадратных уравнений создадим два М-файла – файл-функцию для решения квадратного уравнения и файл-сценарий для создания массива корней уравнений при различных значениях коэффициентов a, b и с.