
|
|
Система А совместна и является определеннойМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования Санкт-Петербургский государственный университет технологии и дизайна СЕВЕРО-ЗАПАДНЫЙ ИНСТИТУТ ПЕЧАТИ
Факультет: Полиграфических технологий и оборудования Специальность:Информационные технологии в медиаиндустрии Форма обучения:очная Кафедра:Информационных и управляющих систем
Отчет Дисциплина: Математика Тема: Линейная алгебра. Решение СЛАУ Выполнил: Студент группы ИМ2 __________ Котикова К. В. (подпись) (Ф.И.О.) Руководитель: ________________ __________ Жихарева А. А. (уч.степень, звание) (подпись) (Ф.И.О.) Дата защиты работы ____________ Оценка _________________________
Даны СЛАУ (B-4):A=
Задание
Проверить совместность системы линейных алгебраических уравнений по теореме Кронекера-Капелли Примечание. Для проверки совместности системы рекомендуется воспользоваться операцией конкатенации массивов (для формирования расширенной матрицы системы) и функциями rank (для определения рангов матрицы, коэффициентов системы и расширенной матрицы) и size (для определения числа неизвестных системы) В случае совместности выяснить является ли она определенной. 1. Если система – определенная, то решить её a) средствами пакета: с помощью оператора деления матриц, с помощью функции linsolve; b) с помощью обратной матрицы; c) методом Крамера; d) методом Гаусса (привести расширенную матрицу системы к треугольному виду с помощью функции rref, после чего из приведенной матрицы выделить вектор решения) Выполнить проверку в одном из случаев 2. Если система является неопределенной, то решить систему a) с помощью оператора деления матриц; b) с помощью функции linsolve; c) с помощью функции solve; d) методом Гаусса. Объяснить результаты, полученные после применения каждой из функций. В каждом случаепо полученным результатам построить · общее решение системы; если это невозможно, объяснить почему; · одно или несколько частных решений системы. Показать, что частные решения одной системы, найденные разными способами, совпадают.
Решение: Скрипт disp('Задание СЛАУ') disp('Вводим СЛАУ') Заглавными буквами обозначены матрицы составленные из коэффициентов левой части системы, а маленькими — вектор-столбцы из правой части СЛАУ A=[2 -1 3; 1 3 -1; 1 -2 2], a=[-4; 11; -7] B=[3 -3 2; 4 -5 2; 1 -2 0], b=[2; 1; 5] C=[2 -3 -4; 7 -9 -1; 5 -6 3], c=[2; 3; 1] disp('Проверка совместности СЛАУ') disp('Вычисляем ранги основной матрицы СЛАУ; создаем расширенные матрицы путем горизонтальной конкатенации, вычисляем их ранги; вычисляем размерность матриц (второе число — это количество неизвестных переменных в системе )') rnA=rank(A); rnB=rank(B); rnC=rank(C); rA=[A a]; rB=[B b]; rC=[C c]; rnrA=rank(rA); rnrB=rank(rB); rnrC=rank(rC); sА=size(A); sB=size(B); sC=size(C); disp('Сравниваем ранги основных, расширенных матриц СЛАУ и количество неизвестных')
if rnA==rnrA if rnA==sА(1,2) disp('Система А совместна и является определенной')
disp('Решение средствами пакета: с помощью оператора деления матриц, с помощью функции linsolve') OtvetA1=A\a OtvetA1_lins=linsolve(A,a) disp('Проверка:') if A*OtvetA1==a disp('Решение найдено верно') else disp('Решение найдено неверно') end disp('Решение с помощью обратной матрицы') if det(A)==0 disp('Метод не применим, тк определитель равен 0') else OtvetA2=inv(A)*a end disp('Решение методом Крамера') if det(A)==0 disp('Метод не применим, тк определитель равен 0') else Matr1=[a A(:,2:3)] ; OprMatr1=det(Matr1); Matr2=[A(:,1) a A(:,3)]; OprMatr2=det(Matr2); Matr3=[A(:,1:2) a ]; OprMatr3=det(Matr3); OtvetA3=[OprMatr1; OprMatr2; OprMatr3]/det(A) end disp('Решение методом Гаусса') rA_priv=rref(rA); sizerA_priv=size(rA_priv); Otvet4=rA_priv(:,sizerA_priv(1, 2))
else disp('Система А совместна и является неопределенной')
disp('Решение с помощью оператора деления матриц') OtvetA1=A\a disp('Решение с помощью функции linsolve') OtvetA2_lins=linsolve(A,a) disp('Решение с помощью функции solve') disp('OtvetA3=') syms x y z; [x y z]=solve('2*x-y+3*z=-4','x+3*y-z=11','x-2*y+2*z=-7') disp('Решение методом Гаусса') rA_priv=rref(rA); sizerA_priv=size(rA_priv); OtvetA4=rA_priv(:,sizerA_priv(1, 2)) end else disp('Система А несовместна и не имеет решения') end; if rnB==rnrB if rnB==sB(1,2) disp('Система B совместна и является определенной')
disp('Решение средствами пакета: с помощью оператора деления матриц, с помощью функции linsolve') OtvetB1=B\b OtvetB1_lins=linsolve(B,b)
disp('Проверка:') if B*OtvetB1==b disp('Решение найдено верно') else disp('Решение найдено неверно') end
disp('Решение с помощью обратной матрицы') if det(B)==0 disp('Метод не применим, тк определитель равен 0') else OtvetB2=inv(B)*b end
disp('Решение методом Крамера') if det(B)==0 disp('Метод не применим, тк определитель равен 0') else Matr1=[b B(:,2:3)]; OprMatr1=det(Matr1); Matr2=[B(:,1) b B(:,3)]; OprMatr2=det(Matr2); Matr3=[B(:,1:2) b]; OprMatr3=det(Matr3); OtvetB3=[OprMatr1; OprMatr2; OprMatr3]/det(B) end
disp('Решение методом Гаусса') rB_priv=rref(rB); sizerB_priv=size(rB_priv); Otvet4=rB_priv(:,sizerB_priv(1, 2))
else ('Система B совместна и является неопределенной') disp('Решение с помощью оператора деления матриц') OtvetB1=B\b
disp('Решение с помощью функции linsolve') OtvetB2_lins=linsolve(B,b)
disp('Решение с помощью функции solve') disp('OtvetB3=') syms x y z; [x y z]=solve('3*x-3*y+2*z=2','4*x-5*y+2*z=1','x-2*y=5')
disp('Решение методом Гаусса') rB_priv=rref(rB); sizerB_priv=size(rB_priv); OtvetB4=rB_priv(:,sizerB_priv(1, 2)) end else disp('Система B несовместна и не имеет решения') end; if rnC==rnrC if (rnC==sC(1,2)) disp('Система C совместна и является определенной')
disp('Решение средствами пакета: с помощью оператора деления матриц, с помощью функции linsolve') OtvetC1=C\c OtvetC1_lins=linsolve(C,c)
disp('Проверка:') if C*OtvetC1==c disp('Решение найдено верно') else disp('Решение найдено неверно') end
disp('Решение с помощью обратной матрицы') if det(C)==0 disp('Метод не применим, тк определитель равен 0') else OtvetC2=inv(C)*c end
disp('Решение методом Крамера') if det(C)==0 disp('Метод не применим, тк определитель равен 0') else Matr1=[c C(:,2:3)]; OprMatr1=det(Matr1); Matr2=[C(:,1) c C(:,3)]; OprMatr2=det(Matr2); Matr3=[C(:,1:2) c ]; OprMatr3=det(Matr3); OtvetC3=[OprMatr1; OprMatr2; OprMatr3]/det(C) end
disp('Решение методом Гаусса') rC_priv=rref(rC); sizerC_priv=size(rC_priv); Otvet4=rC_priv(:,sizerC_priv(1, 2))
else ('Система C совместна и является неопределенной') disp('Решение с помощью оператора деления матриц') OtvetC1=C\c
disp('Решение с помощью функции linsolve') OtvetC2_lins=linsolve(C,c)
disp('Решение с помощью функции solve') disp('OtvetC3=') syms x y z; [x y z]=solve('2*x-3*y-4*z=2','7*x-9*y-z=3','5*x-6*y+3*z=1')
disp('Решение методом Гаусса') rC_priv=rref(rC); sizerC_priv=size(rC_priv); OtvetC4=rC_priv(:,sizerC_priv(1, 2)) end else disp('Система C несовместна и не имеет решения') end Command window >> Задание по СЛАУ Вводим СЛАУ A = 2.00 -1.00 3.00 1.00 3.00 -1.00 1.00 -2.00 2.00 a = -4.00 11.00 -7.00 B = 3.00 -3.00 2.00 4.00 -5.00 2.00 1.00 -2.00 0 b = 2.00 1.00 5.00 C = 2.00 -3.00 -4.00 7.00 -9.00 -1.00 5.00 -6.00 3.00 c = 2.00 3.00 1.00 Проверка совместности СЛАУ Вычисляем ранги основной матрицы СЛАУ; создаем расширенные матрицы путем горизонтальной конкатенации, вычисляем их ранги; вычисляем размерность матриц (второе число — это количество неизвестных переменных в системе ) Сравниваем ранги основных, расширенных матриц СЛАУ и количество неизвестных Система А совместна и является определенной Решение средствами пакета: с помощью оператора деления матриц, с помощью функции linsolve OtvetA1= 1.00 3.00 -1.00 OtvetA1_lins= [ 1] [ 3] [ -1] Проверка: Решение найдено верно Решение с помощью обратной матрицы OtvetA2= 1.00 3.00 -1.00 Решение методом Крамера OtvetA3= 1.00 3.00 -1.00 Решение методом Гаусса Otvet4= 1.00 3.00 -1.00 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
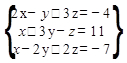 ,B=
,B=  ,C=
,C= 