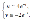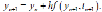|
|
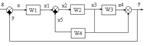
Графы связей и структурные схемы динамических систем.12 В динамической системе, как правило, протекают процессы различной физической природы: механические, гидравлические, электрические, тепловые и т.д. Основой для построения структурной схемы такой системы служат физические законы. Они связывают между собой физические величины внутри системы и внешние силы. Основные уравнения динамической системы мы будем составлять с использованием понятия о динамических звеньях, изучаемых в ТАУ. На первоначальном этапе составления структурной схемы связи между динамическими звеньями удобней представлять в виде графов. Подобно структурным схемам графы связей используются для наглядного изображения физических зависимостей в динамических системах. Между структурной схемой и графом имеется прямое соотношение. Прямоугольник структурной схемы соответствует ребру, а линия передачи сигнала- вершине графа. Обычно при моделировании используют алгебраизированные графы связей. Сравним алгебраизированный граф связи и структурную схему одной и той же системы:
Правило составления графа связи: 1. Номер ребра соответствует номеру передаточной функции звена. 2. Ребро, соединяющее одноименные величины не имеет номера. Передаточная функция такого ребра равна 1. 3. Элементу сравнения на графе соответствует разность, а сумматору- сумма двух величин, равная третьей величине результату. Результат вычитания или суммирования всегда записывают справа от знака равенства. Выбор шага и погрешность решения Одним из важнейших практических вопросов, которые встают перед инженером, составляющим программы решения дифференциальных уравнений, является выбор подходящей величины шага. Если шаг слишком мал, то расчёт потребует неоправданно много машинного времени. Если же наоборот - шаг выбран слишком большим, то значительной будет погрешность, обусловленная усечением рядов, и накопившаяся суммарная ошибка будет также недопустимо большой появления цифровой неустойчивости решения. Обычно, выбирая величину шага, стремятся, чтобы локальная ошибка на шаге была меньше некоторой заданной допустимой величины. Вообще говоря, если порядок точности метода Р, то локальная ошибка определяется выражением: Указанное выражение с помощью О-символики может быть записано более компактно длина шага h будет убывать, а общее из числа N, необходимое для достижения tN, будет возрастать: сумма N локальных ошибок и поэтому мы можем, округляя, записать: раза уменьшает среднюю локальную ошибку примерно в 2p+1 = 4 раза. Но так как для достижения tN теперь потребуется вдвое больше шагов, то глобальная ошибка уменьшится лишь в 2p = 2 раза. Если используется один из методов прогноза и коррекции, то ошибка на шаге определяется величиной последнего члена в формуле коррекции. При использовании же одношаговых методов Рунге - Кутта, локальную ошибку не удается выразить в явной форме. Один из методов оценки этой ошибки основан на двойном счете. Недостатком этого метода является то, что значение yn+1 приходится вычислять дважды, причем второй раз с помощью двух шагов. С другой стороны, главным достоинством методов прогноза и коррекции является простота оценки ошибки на шаге. Жесткие задачи Некоторые обыкновенные дифференциальные уравнения (ДУ) не решаются ни одним из рассмотренных методов. Чтобы понять, почему это так, рассмотрим структуру ДУ. В общем случае ДУ n-го порядка имеют n постоянных времени. Если одна из постоянных времени достаточно мала по сравнению с шагом интегрирования, то задача называется жесткой и ее трудно решить обычными методами. В таких случаях шаг должен быть достаточно мал, чтобы можно было учитывать изменения наиболее быстроизменяющихся членов уравнения. В противном случае решение становится неустойчивым. Если величина шага очень мала по сравнению с интервалом, на котором отыскивается решение, то для получения решения потребуется очень много времени. А накапливающиеся в процессе длительных вычислений погрешности округления могут привести к получению бессмысленного результата. Рассмотрим, например, систему:
После очень небольшого промежутка времени решение весьма близко к функциям: Большинство стандартных методов не приспособлено для решения жестких уравнений. Поэтому были изобретены специальные методы. Простейшим из них является так называемый неявный метод Эйлера, выражаемый формулой
Работу неявного метода Эйлера покажем графически
Разработка эффективных методов для жестких уравнений является областью активных исследований. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 Кроме того, при больших значениях h возникает опасность
Кроме того, при больших значениях h возникает опасность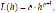 где c некоторая постоянная; h - шаг интегрирования.
где c некоторая постоянная; h - шаг интегрирования.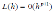 Рассмотрим теперь глобальную ошибку дискретизации в конечной точке t=tN. По мере повышения требований к точности,
Рассмотрим теперь глобальную ошибку дискретизации в конечной точке t=tN. По мере повышения требований к точности,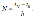 Далее, глобальная ошибка E(h) может быть представлена как
Далее, глобальная ошибка E(h) может быть представлена как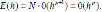 Для метода Эйлера p =1, так что уменьшение длины шага в 2
Для метода Эйлера p =1, так что уменьшение длины шага в 2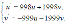 Если u(0) = v(0) =1, то решением будут
Если u(0) = v(0) =1, то решением будут