
|
|
СКАЛЯРНЫЙ И ВЕКТОРНЫЙ ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯМы показали, что ротор магнитного поля отличен от нуля. Такое поле нельзя описывать потенциалом φ, так как оно непотенциально, работа по замкнутому контуру сил поля отлична от нуля. Для описания магнитного поля вводят векторный потенциал
Векторный потенциал Подобно уравнению Пуассона для скалярного потенциала φ (
подставим
Известно из математики, что
где Подставим выражение (5.13) в уравнение Максвелла для
Это соотношение можно переписать в виде Так как ротор вектора Функция φ называется скалярным потенциалом электромагнитного поля. В нестационарном случае она зависит от радиус-вектора точки Таким образом, напряженность электрического поля в общем случае определяется не только скалярным потенциалом φ, но и векторным потенциалом
Второе слагаемое Найдем уравнения, с помощью которых можно вычислить потенциалы
где
Из третьего уравнения Максвелла
Но, учитывая, что
или
Уравнения (5.15) – это и есть искомые уравнения для Потенциалы Рассмотрим самый общий вид калибровочных преобразований потенциалов
Чтобы при этом не изменилось электрическое поле
где f - та же функция. Поле
Здесь использовано Таким образом, эти преобразования не меняют полей На практике часто применяется калибровка, называемая условием Лоренца:
Для поля в вакууме условие Лоренца принимает вид:
Покажем, что условие (5.18) может быть удовлетворено надлежащим выбором функции f в формулах (5.16) и (5.17). Для этого подставим в уравнение (6) значения φ΄ и
здесь
где Условие Лоренца сильно ограничивает набор значений потенциалов, пригодных для описания данного поля, но все же не делает выбор потенциалов вполне однозначным. Действительно, не нарушая условия (5.18), можно осуществить преобразования
при этом оба набора потенциалов предполагаются удовлетворяющими условию Лоренца. Функция ψ является решением уравнения
Действительно, подставив в левую часть выражения (5.18) вместо
которое согласно (5.18) и (5.20) равно нулю. Таким образом, если В качестве дополнительного условия также может быть принято требование
Из (5.19) следует, что Лоренцева калибровка, удовлетворяющая дополнительному условию (5.21) называется кулоновской или поперечной калибровкой. В случае этой калибровки скалярный потенциал удовлетворяет уравнению Пуассона
т.е. является кулоновским потенциалом (отсюда и название «кулоновская калибровка»).
УРАВНЕНИЕ ДАЛАМБЕРА При соблюдении условий ((5.18) последнее слагаемое в первом из уравнений (5.15) обращается в ноль. Кроме того, производная по времени от
следовательно,
Таким образом, вместо двух взаимосвязанных уравнений мы получили два раздельных уравнения, причем уравнения для Дифференциальное уравнение вида
называется уравнением Даламбера. Его можно записать очень компактно, если ввести оператор Даламбера ٱ Тогда уравнение (5. 24) принимает вид ٱ f= В стационарном случае производные по времени обращаются в ноль, и уравнение Даламбера переходит в уравнение Пуассона. С использованием символа ٱ (Даламбера) уравнения (5.22) и (5.23) принимают вид ٱ Эти уравнения описывают электромагнитные поля проще, чем уравнения Максвелла, поэтому бывает легче вычислить потенциалы Из уравнений Максвелла следует, что электромагнитное поле способно существовать в отсутствие электрических зарядов и токов. При этом уравнение его состояния обязательно носит волновой характер. Поле такого рода называют электромагнитными волнами.
Лекция 22 5.9.ЭНЕРГИЯ И ИМПУЛЬС ЭЛЕКТРОМАГНИТНОГО ПОЛЯ СОХРАНЕНИЕ ЭНЕРГИИ И ИМПУЛЬСА В ИЗОЛИРОВАННОЙ СИСТЕМЕ ПРОИЗВОЛЬНО ДВИЖУЩИХСЯ ЗАРЯДОВ Как всякий материальный объект, электромагнитное поле обладает импульсом, энергией и моментом импульса. Эти величины для поля сохраняются, если оно оказывается изолированным. Условие изолированности выполняется в тех случаях, когда в области существования поля нет электрических зарядов и токов. Такое поле называется свободным. Сохранение энергии, импульса и момента импульса изолированного поля является следствием однородности пространства и времени и изотропности пространства. При взаимодействии электромагнитного поля с зарядами и токами сохраняются суммарные величины для поля и заряженных частиц. Так, сохраняется полная сумма импульсов электромагнитного поля и заряженных частиц. Поскольку поле всегда занимает некоторую область пространства, энергия, импульс и момент импульса всегда характеризуются их удельными значениями, т.е. соответствующей величиной, отнесенной к единице объема в данном месте пространства. Эти величины называются соответственно плотностью энергии w, импульса Из уравнений Максвелла-Лоренца можно получить значения этих плотностей и законы их сохранения.
5.10. РАБОТА, СОВЕРШАЕМАЯ ПОЛЕМ ПРИ ПЕРЕМЕЩЕНИИ ЗАРЯДОВ Определения кинетической и потенциальной энергии, а также импульса и момента импульса, данные в механике для материальной точки и системы материальных точек, отнюдь не распространяются на поля. Рассмотрим систему заряженных материальных точек, взаимодействующих между собой. Такая система описывается уравнениями Максвелла-Лоренца. Пользуясь этими уравнениями, распространим понятия энергии и импульса на поля, находя величины, сохраняющиеся для изолированной системы поле - заряды. Макроскопические электрические заряды, так или иначе, связаны с материальными телами, на которых они расположены. Пусть частица массой
Умножим это выражение на
В правой части этого выражения стоит работа силы Лоренца. Она совершается только электрической составляющей этой силы, так как магнитная составляющая равна нулю ( векторы Левую часть преобразуем с помощью тождества
Действительно,
в правой части
Тогда окончательно получаем
- элементарная работа силы Лоренца равна приросту релятивистской кинетической энергии заряженной материальной точки. Просуммируем теперь элементарные работы по всем точкам системы и разделим на dt:
( здесь на dt разделили левую и правую части). Формула (5.23) выражает теорему об изменении энергии системы материальных точек в единицу времени за счет работы поля, совершенной над ними. Выведенная формула для точечного заряда обобщается и на случай непрерывно распределенного в пространстве заряда. Для работы поля в единицу времени имеем:
причем
Мощность, заключенная в единице объема ( плотность мощности) равна
Итак, за счет работы поля изменяется кинетическая энергия находящихся в поле заряженных частиц. При этом энергия поля превращается в кинетическую энергию частиц. 5.11. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ. ПЛОТНОСТЬ И ПОТОК ЭНЕРГИИ. ЗАКОН ИЗМЕНЕНИЯ ЭНЕРГИИ Найдем энергию электромагнитного поля по заданным значениям векторов
Умножим первое уравнение на
Из равенства (5.28) вычтем (5.29), имеем
Из математики известно, что Левая часть выражения (5.30) есть частная производная по времени от функции или
Проинтегрируем это выражение по объему V:
Преобразуем:
Но Тогда энергия поля в заданном объеме V равна
Поток энергии поля через замкнутую поверхность в единицу времени определяет полную мощность излучения системы зарядов и равен
Таким образом, равенство (5.31) – это математическое выражение закона изменения энергии электромагнитного поля. Его можно переписать в виде:
(W не зависит от координат точек поля и частную производную можно заменить полной). Теорема (5.32) читается так: убыль энергии в некотором объеме равна потоку энергии, выходящему из объема, и работе , совершаемой полем над зарядами в этом объеме. В дифференциальной форме эта теорема имеет вид:
В области, где нет зарядов и токов (
Это уравнение является локальным выражением закона сохранения энергии для электромагнитного поля при отсутствии зарядов. Оно выражает теорему Пойтинга. Проинтегрируем (5.33) по объему V, ограничивающему поверхность s:
Таким образом, при отсутствии зарядов убыль энергии поля в объеме V в единицу времени равна интегральному потоку энергии через поверхность, ограничивающую этот объем. Если потока энергии через границы поля нет,
5.12. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ДЛЯ ИЗОЛИРОВАННОЙ СИСТЕМЫ ПОЛЕ – ЗАРЯДЫ Рассмотрим изолированную систему поле-заряды. Изолированность системы следует понимать как отсутствие потока энергии через ограничивающую ее поверхность и отсутствие потока массы , который тоже уносил бы энергию. В таком случае убыль энергии электромагнитного поля в единицу времени равна
- работе, совершаемой полем над зарядами. Ясно, что работа, производимая над зарядами, является мерой превращения энергии поля в другие виды: в кинетическую энергию заряженных частиц и тел, потенциальную энергию деформации, внутреннюю энергию среды и т.д. Для дискретной системы зарядов
тогда подставляя в (5.31) выражение (5.25), получаем
Из этого выражения следует, что
В последнем равенстве объем V может быть или конечным, или охватывать все пространство. Это соотношение выражает закон сохранения энергии в изолированной системе поле-заряды: в изолированной системе поле-заряды сохраняется сумма энергии поля и релятивистской энергии заряженных материальных точек.
5.13. ИМПУЛЬС ЭЛЕКТРОМАГНИТНОГО ПОЛЯ. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА Просуммируем все уравнения движения частиц, находящихся в поле, в выражении (5.24)
Будем считать распределение зарядов в пространстве непрерывным, поэтому сумму заменим интегралом по объему системы:
Подставим значения
Чтобы в правой части этого равенства получить производную по времени, дополним его слагаемым
Таким образом, равенство (5.35) не нарушается. Кроме того, добавим еще
Сгруппируем:
Подставив в выражение (5.34), получаем
В случае изолированной системы поле-заряды второй и третий интегралы можно свести к поверхностным, и при интегрировании по всему пространству они дают 0. В результате имеем
или
- это закон сохранения импульса для изолированной системы поле-заряды. Величина
есть плотность импульса. Выражение (5.36) можно сформулировать так: в изолированной системе поле-заряды полный импульс, равный релятивистскому импульсу заряженных частиц и импульсу электромагнитного поля, сохраняется. Из выражения (5. 37) следует, что плотность импульса Взаимодействие между заряженными телами осуществляется посредством поля. Это приводит к несохранению импульса замкнутой механической системы материальных точек, если система обменивается импульсом с полем так, что импульс поля изменяется. В такой системе может не выполняться третий закон Ньютона. Например, излучающее, рассеивающее, отражающее или поглощающее электромагнитные волны тело испытывает со стороны поля действие силы, т.к. импульс тела меняется, но эта сила не имеет противодействующей – к полю не может быть приложена сила. Обладая импульсом, электромагнитное поле оказывает давление на тела, с которыми взаимодействует. Примером тому – световое давление. Плотность момента импульса электромагнитного поля найдем по правилу, известному из механики:
где
Из (5.37) следует, что 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
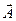 , причем
, причем (5.13)
(5.13)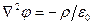 ), запишем уравнение для векторного потенциала
), запишем уравнение для векторного потенциала 
 ,
,  . Имеем:
. Имеем: .
. Дивергенция от ротора равна нулю,
Дивергенция от ротора равна нулю,  , тогда
, тогда  , или
, или
 - оператор Лапласа.
- оператор Лапласа. :
:

 равен нулю, этот вектор можно представить в виде градиента некоторой функции φ:
равен нулю, этот вектор можно представить в виде градиента некоторой функции φ: 
 и времени t. Потенциалы φ и
и времени t. Потенциалы φ и  имеют одинаковую размерность.
имеют одинаковую размерность. (5.14)
(5.14) обусловлено явлением электромагнитной индукции. В случае стационарного поля
обусловлено явлением электромагнитной индукции. В случае стационарного поля 

 - скорость света в среде, имеем
- скорость света в среде, имеем
 . Подставим
. Подставим 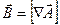 и
и  :
:
 и
и  , имеем
, имеем
 (5.15)
(5.15) и
и  . Выбор потенциалов следует осуществлять наиболее удобным для данного случая образом. Такой наиболее целесообразный выбор потенциалов называется их калибровкой.
. Выбор потенциалов следует осуществлять наиболее удобным для данного случая образом. Такой наиболее целесообразный выбор потенциалов называется их калибровкой. не изменится, если к
не изменится, если к 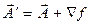
 (5.16)
(5.16) ), нужно совершить переход от φ к φ΄
), нужно совершить переход от φ к φ΄ (5.17)
(5.17) , определяемое потенциалами φ΄ и
, определяемое потенциалами φ΄ и  , в этом случае равно
, в этом случае равно .
.
 (5.18)
(5.18)

 Получаем уравнение для нахождения функции f
Получаем уравнение для нахождения функции f
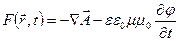 - есть заданная функция
- есть заданная функция 
 (5.19)
(5.19) (5.20)
(5.20) и φ штрихованные потенциалы из (5.19), получим выражение
и φ штрихованные потенциалы из (5.19), получим выражение
 и φ` принадлежат той же калибровке. Это обстоятельство позволяет наложить на потенциалы кроме условия (5.18) еще одно дополнительное условие. Например, можно потребовать, чтобы
и φ` принадлежат той же калибровке. Это обстоятельство позволяет наложить на потенциалы кроме условия (5.18) еще одно дополнительное условие. Например, можно потребовать, чтобы  . Для этого, согласно второму из уравнений (5.18), достаточно выбрать функцию ψ так, чтобы ее производная по времени была равна φ.
. Для этого, согласно второму из уравнений (5.18), достаточно выбрать функцию ψ так, чтобы ее производная по времени была равна φ. (5.21)
(5.21) поэтому для выполнения требования
поэтому для выполнения требования  необходимо соблюдение равенства
необходимо соблюдение равенства  месте с тем, из (5.20) имеем
месте с тем, из (5.20) имеем  поэтому, если взять в качестве ψ решение уравнения
поэтому, если взять в качестве ψ решение уравнения  и подставить это решение в (5.19), мы получим значения потенциалов φ΄ и
и подставить это решение в (5.19), мы получим значения потенциалов φ΄ и 
 имеет значение
имеет значение
 (5.22)
(5.22) (5.23)
(5.23) и φ приобрели сходную форму.
и φ приобрели сходную форму. (5.24)
(5.24)
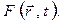
 ٱ
ٱ 
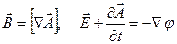 вычислить
вычислить  и
и  .
. , и момента импульса
, и момента импульса  . Каждая из этих функций зависит от времени t и радиус-вектора
. Каждая из этих функций зависит от времени t и радиус-вектора  несет заряд
несет заряд  . Тогда по второму закону Ньютона уравнения движения имеют вид:
. Тогда по второму закону Ньютона уравнения движения имеют вид: . (5.25)
. (5.25) , получим выражение для энергии
, получим выражение для энергии
 и
и  .
. , тогда в левой части
, тогда в левой части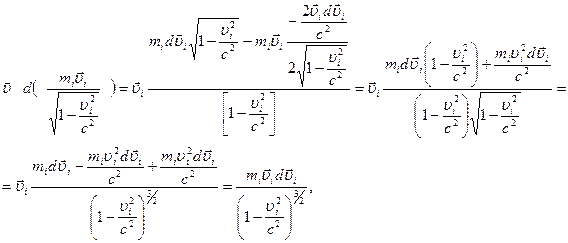


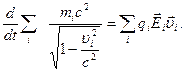 (5.26)
(5.26)
 - плотность тока,
- плотность тока,  - заряд одного носителя,
- заряд одного носителя, 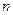 - число носителей в единице объема. Тогда
- число носителей в единице объема. Тогда . (5.27)
. (5.27)
 и
и 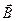 . Для этого используем уравнения Максвелла
. Для этого используем уравнения Максвелла
 , второе – на
, второе – на 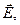 получаем
получаем
 (5.30)
(5.30)
 Тогда имеем:
Тогда имеем: 

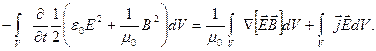
 Получаем
Получаем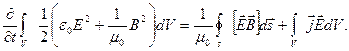 (5.31)
(5.31) - работа поля за единицу времени в пределах конечного объема V. Тогда
- работа поля за единицу времени в пределах конечного объема V. Тогда  - плотность энергии электромагнитного поля. Она равна сумме плотностей энергий электрического и магнитного полей.
- плотность энергии электромагнитного поля. Она равна сумме плотностей энергий электрического и магнитного полей.  - плотность потока энергии, называемая вектором Пойтинга. Этот вектор направлен в сторону перемещения энергии и по абсолютному значению равен энергии, которая в единицу времени переносится полем через единичную площадку, ориентированную перпендикулярно потоку.
- плотность потока энергии, называемая вектором Пойтинга. Этот вектор направлен в сторону перемещения энергии и по абсолютному значению равен энергии, которая в единицу времени переносится полем через единичную площадку, ориентированную перпендикулярно потоку.

 (5.32)
(5.32)
 ), плотность электромагнитной энергии связана с ее потоком
), плотность электромагнитной энергии связана с ее потоком  уравнением непрерывности:
уравнением непрерывности: (5.33)
(5.33)
 , и энергия поля убывает, если
, и энергия поля убывает, если  - заряды движутся под действием сил поля. Если же
- заряды движутся под действием сил поля. Если же 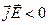 , то энергия поля растет, но в этом случае работают не силы поля, а сторонние силы, не сводящиеся к силе Лоренца.
, то энергия поля растет, но в этом случае работают не силы поля, а сторонние силы, не сводящиеся к силе Лоренца.

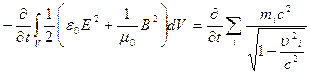 .
.
 (5.34)
(5.34) и
и  из уравнений Максвелла:
из уравнений Максвелла: . (5.35)
. (5.35) . Это равенство всегда равно нулю, так как
. Это равенство всегда равно нулю, так как  , т.е.
, т.е.  , тогда
, тогда
 . Очевидно,
. Очевидно, 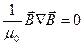 , так как
, так как  . Получаем:
. Получаем:

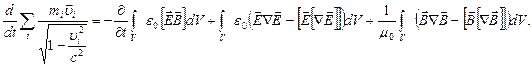
 ,
, (5.36)
(5.36) (5.37)
(5.37) отлична от нуля только в том случае, если существуют оба поля
отлична от нуля только в том случае, если существуют оба поля  и
и  , непараллельные друг другу.
, непараллельные друг другу.
 - радиус-вектор точки, в которой определяются
- радиус-вектор точки, в которой определяются  . Умножая (5.37) векторно справа на
. Умножая (5.37) векторно справа на 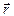 , получаем закон сохранения момента импульса в изолированной системе поле-заряды:
, получаем закон сохранения момента импульса в изолированной системе поле-заряды: .
. .
.