Бесконечно большие функции
Основные элементарные функции
Основными элементарными функциями являются:
1) степенная функция:  R; R;
частные случаи:
а)  (рис.1) (рис.1)
область определения –  R; R;
множество значений –  R; R;
б)  (рис.2) (рис.2)
область определения –  R; R;
множество значений –  ; ;
б)  (рис.3) (рис.3)
область определения – 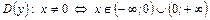 ; ;
множество значений –  ; ;
в)  (рис.4) (рис.4)
область определения –  ; ;
множество значений –  ; ;
 рис.1 рис.1  рис.2 рис.2
 рис.3 рис.3  рис.4 рис.4
2) показательная функция:  (рис.5); (рис.5);
частный случай:  ; ;
область определения –  R; R;
множество значений –  ; ;
3) логарифмическая функция:  (рис.6); (рис.6);
частный случай: 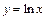 ; ;
область определения –  ; ;
множество значений –  R; R;
 рис.5 рис.5  рис.6 рис.6
4) тригонометрические функции:
а)  (рис.7) (рис.7)
область определения –  R; R;
множество значений –  ; ;
б)  (рис.8) (рис.8)
область определения –  R; R;
множество значений –  ; ;
в)  (рис.9) (рис.9)
область определения –  , ,  Z; Z;
множество значений –  R; R;
г)  (рис.10) (рис.10)
область определения –  , ,  Z; Z;
множество значений –  R; R;
 
рис.7 рис.8
 
рис.9 рис.10
5) обратные тригонометрические функции:
а)  (рис.11) (рис.11)
область определения –  ; ;
множество значений –  ; ;
б)  (рис.12) (рис.12)
область определения –  ; ;
множество значений – 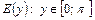 ; ;
в)  (рис.13) (рис.13)
область определения –  R; R;
множество значений –  ; ;
г)  (рис.14) (рис.14)
область определения –  R; R;
множество значений –  . .
 рис.11 рис.11  рис.12 рис.12
 
рис.13 рис.14
Гиперболические функции:
1) гиперболический синус  (рис.15); (рис.15);
2) гиперболический косинус  (рис.16); (рис.16);
3) гиперболический тангенс  (рис.17); (рис.17);
4) гиперболический тангенс  (рис.18). (рис.18).
 рис.15 рис.15  рис.16 рис.16
 
рис.17 рис.18
Пример 1. Найдите область определения функций:
1)  ; 2) ; 2)  . .
Решение.
1) Учитывая область определения функции  , получим: , получим:
       
  : :  . .
2) Учитывая область определения функций  и и 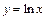 , получим систему неравенств: , получим систему неравенств:
  
Решая полученную систему методом интервалов (рис.19), получим искомую область определения функции  : :  . .
 рис.19 рис.19
Ответ: 1)  ; 2) ; 2)  . .
1.2. Преобразования графика функции. Числовые промежутки
Преобразования графика функции
1. График функции  получается из графика функции получается из графика функции  сдвигом вдоль оси Oy на сдвигом вдоль оси Oy на  единиц (вверх, если единиц (вверх, если  , и вниз, если , и вниз, если  ). ).
2. График функции  получается из графика функции получается из графика функции  сдвигом вдоль оси Oх на сдвигом вдоль оси Oх на  единиц (вправо, если единиц (вправо, если  , и влево, если , и влево, если  ). ).
3. График функции  получается из графика функции получается из графика функции  растяжением (сжатием) вдоль оси Oy в k раз ( растяжением (сжатием) вдоль оси Oy в k раз (  раз), если раз), если  ( (  ). ).
4. График функции  получается из графика функции получается из графика функции  сжатием (растяжением) вдоль оси Oх в m раз ( сжатием (растяжением) вдоль оси Oх в m раз (  раз), если раз), если  ( (  ). ).
5. График функции  получается из графика функции получается из графика функции  симметричным отражением относительно оси Ох. симметричным отражением относительно оси Ох.
6. График функции  получается из графика функции получается из графика функции  симметричным отражением относительно оси Оу. симметричным отражением относительно оси Оу.
7. График функции  получается из графика функции получается из графика функции  симметричным отражением относительно оси Ох части графика, находящегося в нижней полуплоскости. симметричным отражением относительно оси Ох части графика, находящегося в нижней полуплоскости.
8. График функции  получается из графика функции получается из графика функции  симметричным отражением относительно оси Ох части графика, находящегося в верхней полуплоскости. симметричным отражением относительно оси Ох части графика, находящегося в верхней полуплоскости.
Числовые промежутки. Окрестность точки
Пусть a и b – действительные числа, причем  . .
Числовыми промежутками (интервалами) называются подмножества всех действительных чисел, имеющих следующий вид:
 – отрезок (сегмент, замкнутый промежуток); – отрезок (сегмент, замкнутый промежуток);
 – интервал (открытый промежуток); – интервал (открытый промежуток);
 – полуоткрытые интервалы; – полуоткрытые интервалы;
бесконечные интервалы (промежутки):
 ; ;  ; ;
 ; ;  ; ;
 R. R.
Пусть a – любое действительное число (точка на числовой прямой).  – окрестностью – окрестностью  точки точки  называется интервал называется интервал  , где , где  – сколь угодно малое положительное число. Число а называется центром окрестности, а число – сколь угодно малое положительное число. Число а называется центром окрестности, а число  – радиусом окрестности. – радиусом окрестности.
Если  , то выполняется неравенство , то выполняется неравенство   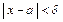 (рис.20а). (рис.20а).
Если  , то неравенство , то неравенство  определяет проколотую определяет проколотую  – окрестность – окрестность  точки точки  (рис.20б). (рис.20б).
 
рис.20а рис.20б
1.3. Бесконечно малые функции. Предел функции в точке. Свойства пределов
Бесконечно малые функции
Определение. Функция  называется бесконечно малой функцией (б.м.ф.) при называется бесконечно малой функцией (б.м.ф.) при  , если для любого сколь угодно малого положительного числа , если для любого сколь угодно малого положительного числа  существует положительное число существует положительное число  такое, что для всех x из проколотой такое, что для всех x из проколотой  – окрестности точки – окрестности точки  выполняется неравенство выполняется неравенство  . .
Это определение можно кратко записать так:
 – б.м.ф. при – б.м.ф. при  
  . .
Свойства бесконечно малых функций:
1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
2. Произведение ограниченной функции на бесконечно малую функцию есть бесконечно малая функция.
3. Произведение двух бесконечно малых функций есть бесконечно малая функция.
4. Произведение бесконечно малой функции на число есть бесконечно малая функция.
5. Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.
Предел функции в точке
Пусть функция  определена в некоторой окрестности точки определена в некоторой окрестности точки  , кроме, быть может, самой точки , кроме, быть может, самой точки  . .
Определение 1. Число А называется пределом функции 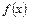 в точке в точке  (или при (или при  ), если разность ), если разность  является бесконечно малой функцией при является бесконечно малой функцией при  , т.е. если , т.е. если  , где , где  – б.м.ф. при – б.м.ф. при  , то , то  . .
Определение 2. Число А называется пределом функции 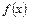 в точке в точке  (или при (или при  ), если для любого сколь угодно малого положительного числа ), если для любого сколь угодно малого положительного числа  существует положительное число существует положительное число  такое, что для всех x из проколотой такое, что для всех x из проколотой  – окрестности точки – окрестности точки  выполняется неравенство выполняется неравенство  , т.е. , т.е.  . .
Это определение можно кратко записать так:
 
  . .
Из определения 1 следует, что если число А является пределом функции 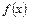 в точке в точке  (или при (или при  ), то функцию ), то функцию 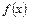 можно представить в виде суммы числа А и бесконечно малой функции можно представить в виде суммы числа А и бесконечно малой функции  при при  . Верно и обратное, т.е. . Верно и обратное, т.е.
 , где , где  – б.м.ф. при – б.м.ф. при    . .
Если функция  – бесконечно малая функция при – бесконечно малая функция при  , то ее предел в точке , то ее предел в точке  равен нулю, т.е. равен нулю, т.е.  . .
Геометрический смысл предела функции в точке:  , если для любой , если для любой  – окрестности точки – окрестности точки  найдется такая найдется такая  – окрестность точки – окрестность точки  , что для всех , что для всех  из этой из этой  – окрестности соответствующие значения функции – окрестности соответствующие значения функции  лежат в лежат в  – окрестности точки – окрестности точки  . Точки графика функции . Точки графика функции  лежат внутри полосы шириной лежат внутри полосы шириной 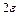 , ограниченной прямыми , ограниченной прямыми  и и  (рис.21). (рис.21).
 рис.21 рис.21
Свойства пределов функций:
Пусть функции 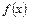 и и  имеют пределы при имеют пределы при  : :  и и  . Тогда: . Тогда:
1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:
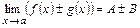 . .
2. Функция может иметь только один предел при  . .
3. Предел числа равен этому же числу:
 число. число.
4. Предел произведения двух функций равен произведению их пределов:
 . .
5. Постоянный множитель можно выносить за знак предела:
 . .
6. Предел степени с натуральным показателем равен той же степени предела:
 , , 
7. Предел частного двух функций равен частному их пределов, если предел делителя не равен нулю:
.
8. Если  – сложная функция, то – сложная функция, то  . .
1.4. Предел функции при  . Бесконечно большие функции . Бесконечно большие функции
Определение. Пусть функция  определена в промежутке определена в промежутке  . Число А называется пределом функции . Число А называется пределом функции 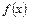 при при  , если для любого сколь угодно малого положительного числа , если для любого сколь угодно малого положительного числа  существует такое положительное число существует такое положительное число  , что при , что при
всех  , удовлетворяющих неравенству , удовлетворяющих неравенству  , выполняется неравенство , выполняется неравенство  , т.е. , т.е.  . .
Это определение можно кратко записать так:
  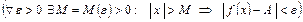 . .
Бесконечно большие функции
Определение. Функция  называется бесконечно большой функцией (б.б.ф.) при называется бесконечно большой функцией (б.б.ф.) при  , если для любого числа , если для любого числа  существует такое число существует такое число  , что для что для всех x из проколотой , что для что для всех x из проколотой  – окрестности точки – окрестности точки  выполняется неравенство выполняется неравенство  . .
Коротко:
 – б.б.ф. при – б.б.ф. при  
  

Например, функция  – б.б.ф. при – б.б.ф. при  . .
Определение. Функция  называется бесконечно большой функцией (б.б.ф.) при называется бесконечно большой функцией (б.б.ф.) при  , если для любого числа , если для любого числа  существует такое число существует такое число  , что для что для всех x, удовлетворяющих неравенству , что для что для всех x, удовлетворяющих неравенству  , выполняется неравенство , выполняется неравенство  , т.е. , т.е.  . .
Коротко:
 – б.б.ф. при – б.б.ф. при  
  

Например, функция  – б.б.ф. при – б.б.ф. при  и б.м.ф. при и б.м.ф. при  , т.е. при , т.е. при   и и  . При . При   и и  . .
Многочлен n-ой степени  – б.б.ф. при – б.б.ф. при  , т.е. , т.е.  . .
Связь между бесконечно малой и бесконечно большой функциями: если функция  – бесконечно малая при – бесконечно малая при  ( (  ), то функция ), то функция  – бесконечно большая при – бесконечно большая при  , и наоборот, если функция , и наоборот, если функция 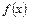 – бесконечно большая при – бесконечно большая при  , то функция , то функция  – бесконечно малая при – бесконечно малая при  : :
 ; ;
 . .
Для того чтобы найти предел элементарной функции, когда аргумент стремится к значению, принадлежащему области определения этой функции, нужно в выражение функции вместо аргумента подставить его предельное значение.
Пример 2. Вычислите пределы:
1)  ; 2) ; 2)  ; 3) ; 3)  . .
Решение.
1) Подставляем вместо  его предельное значение 3, получим его предельное значение 3, получим
 . .
2) Знаменатель дроби  при при  является бесконечно малой величиной, тогда по теореме о связи бесконечно малой и бесконечно большой функциями получим является бесконечно малой величиной, тогда по теореме о связи бесконечно малой и бесконечно большой функциями получим
 . .
3) Знаменатель дроби  при при  является бесконечно большой величиной, тогда по теореме о связи бесконечно малой и бесконечно большой функциями получим является бесконечно большой величиной, тогда по теореме о связи бесконечно малой и бесконечно большой функциями получим
 . .
Ответ. 1) 8; 2) 0; 3)  . .
1.5. Раскрытие неопределённостей вида  . .
Раскрытие неопределенностей вида  , ,  , ,  , , 
Далеко не всякая подстановка предельного значения в функцию вместо независимой переменной может сразу привести к нахождению предела. Случаи, в которых подстановка предельного значения в функцию не дает значения предела, называют неопределенностями; к ним относятся неопределенности видов
 , ,  , ,  , ,  , ,  , ,  , ,  . .
Устранить, т.е. раскрыть, неопределенность удается часто с помощью алгебраических преобразований.
Неопределенность вида 
Рассмотрим пределы вида  с неопределенностью вида с неопределенностью вида  , где , где  и и  – многочлены степени n и m соответственно. – многочлены степени n и m соответственно.
Правило 1. Для раскрытия неопределенности вида  необходимо вынести за скобку в числителе и знаменателе дроби необходимо вынести за скобку в числителе и знаменателе дроби  с наибольшим показателем степени среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется. с наибольшим показателем степени среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется.
Правило 2.
1) Если степень n числителя больше степени m знаменателя дроби 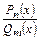 , т.е. , т.е.  , то , то  ; ;
2) если  , то , то  ; ;
3) если  , то , то  , где , где  и и  – старшие коэффициенты многочленов – старшие коэффициенты многочленов  и и  соответственно. соответственно.
Пример 3. Вычислите  . .
Решение.
1-й способ.  . Вынося за скобку и в числителе и в знаменателе . Вынося за скобку и в числителе и в знаменателе  в наибольшей степени, получим в наибольшей степени, получим

 . .
2-й способ. Степени числителя и знаменателя дроби равны, тогда по правилу 2 получим
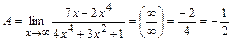 . .
Ответ:  . .
Пример 4. Вычислите  . .
Решение.
1-й способ.  . Вынося за скобку и в числителе и в знаменателе . Вынося за скобку и в числителе и в знаменателе  в наибольшей степени, получим в наибольшей степени, получим
 . .
2-й способ. Степень числителя меньше степени знаменателя (  , ,  ), тогда по правилу 2 получим ), тогда по правилу 2 получим
 . .
Ответ: 0.
Пример 5. Вычислите  . .
Решение.
1-й способ.  . Вынося за скобку и в числителе и в знаменателе . Вынося за скобку и в числителе и в знаменателе  в наибольшей степени, получим в наибольшей степени, получим

 . .
2-й способ. Степень числителя больше степени знаменателя (  , ,  ), тогда по правилу 2 получим ), тогда по правилу 2 получим
 . .
Ответ:  . .
Пример 6. Вычислите  . .
Решение.  . Чтобы выяснить, какова наибольшая степень среди слагаемых дроби, следует сначала вынести . Чтобы выяснить, какова наибольшая степень среди слагаемых дроби, следует сначала вынести  с наибольшим показателем степени в выражениях под знаком радикала: с наибольшим показателем степени в выражениях под знаком радикала:
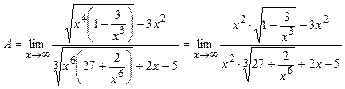 . .
Наибольшая степень вторая; вынося за скобку  , получим , получим

 . .
Ответ:  . .
1.6. Раскрытие неопределённостей вида  . .
Неопределенность вида 
Случай 1. Рассмотрим пределы вида  с неопределенностью вида с неопределенностью вида  , где , где  и и  – многочлены степени n и m соответственно. – многочлены степени n и m соответственно.
Правило 1. Для раскрытия неопределенности вида  необходимо разложить и числитель и знаменатель дроби на множители. После сокращения дроби на множитель необходимо разложить и числитель и знаменатель дроби на множители. После сокращения дроби на множитель  неопределенность устраняется. Правило можно применять неоднократно. неопределенность устраняется. Правило можно применять неоднократно.
Замечание. Если число  является корнем многочлена является корнем многочлена  , то многочлен можно разложить на множители по формуле , то многочлен можно разложить на множители по формуле  , где , где  – многочлен степени n-1, полученный делением «уголком» многочлена – многочлен степени n-1, полученный делением «уголком» многочлена  на на  . Также многочлен можно разложить на множители методом группировки слагаемых. Если квадратный трехчлен . Также многочлен можно разложить на множители методом группировки слагаемых. Если квадратный трехчлен  имеет корни имеет корни  и и  , то разложение этого трехчлена на множители примет вид , то разложение этого трехчлена на множители примет вид  . .
Пример 7. Вычислите  . .
Решение. Имеем неопределенность вида  . Знаменатель имеет корни . Знаменатель имеет корни  и и  . Разложив числитель и знаменатель дроби на множители, получим . Разложив числитель и знаменатель дроби на множители, получим

 . .
Ответ:  . .
Пример 8. Вычислите  . .
Решение. Имеем неопределенность вида  . Числитель имеет корни . Числитель имеет корни  и и  . Используя метод группировки слагаемых, получим разложение знаменателя на множители: . Используя метод группировки слагаемых, получим разложение знаменателя на множители:
 . .
Тогда

 . .
Ответ:  . .
Случай 2. Рассмотрим пределы вида  с неопределенностью вида с неопределенностью вида  , где функции , где функции 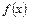 и и  (или одна из них) содержат иррациональность. (или одна из них) содержат иррациональность.
Правило 2. Для раскрытия неопределенности вида  необходимо избавиться от иррациональности, умножив и числитель и знаменатель дроби на сопряженный множитель. После сокращения дроби на множитель необходимо избавиться от иррациональности, умножив и числитель и знаменатель дроби на сопряженный множитель. После сокращения дроби на множитель  неопределенность устраняется. неопределенность устраняется.
Замечание. Для иррациональности  сопряженный множитель имеет вид сопряженный множитель имеет вид  , при этом , при этом  . Для иррациональности . Для иррациональности  сопряженным является множитель сопряженным является множитель  , при этом , при этом  . .
Пример 9. Вычислите  . .
Решение. Имеем неопределенность вида  . Для того чтобы избавиться от иррациональности, умножим и числитель и знаменатель дроби на сопряженный множитель . Для того чтобы избавиться от иррациональности, умножим и числитель и знаменатель дроби на сопряженный множитель  . Тогда . Тогда
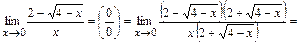
 . .
Ответ:  . .
Пример 10. Вычислите  . .
Решение. Имеем неопределенность вида  . Для того чтобы избавиться от иррациональности, умножим и числитель и знаменатель дроби на сопряженные множители . Для того чтобы избавиться от иррациональности, умножим и числитель и знаменатель дроби на сопряженные множители  и и  . Тогда . Тогда


 . .
Ответ:  . .
Пример 11. Вычислите  . .
Решение. Имеем неопределенность вида  . Для того чтобы избавиться от иррациональности, умножим и числитель и знаменатель дроби на сопряженный множитель . Для того чтобы избавиться от иррациональности, умножим и числитель и знаменатель дроби на сопряженный множитель  . Тогда . Тогда

 . .
Ответ:  . .
1.7. Первый замечательный предел
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 R;
R; (рис.1)
(рис.1) R;
R; R;
R; (рис.2)
(рис.2) R;
R; ;
; (рис.3)
(рис.3)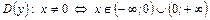 ;
; ;
; (рис.4)
(рис.4) ;
; рис.1
рис.1  рис.2
рис.2 рис.3
рис.3  рис.4
рис.4 (рис.5);
(рис.5); ;
; ;
; (рис.6);
(рис.6);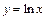 ;
; ;
; R;
R; рис.5
рис.5  рис.6
рис.6 (рис.7)
(рис.7) ;
; (рис.8)
(рис.8) (рис.9)
(рис.9) ,
,  Z;
Z; R;
R; (рис.10)
(рис.10) ,
, 



 (рис.11)
(рис.11) ;
; ;
; (рис.12)
(рис.12)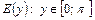 ;
; (рис.13)
(рис.13) ;
; (рис.14)
(рис.14) .
. рис.11
рис.11  рис.12
рис.12

 (рис.15);
(рис.15); (рис.16);
(рис.16); (рис.17);
(рис.17); (рис.18).
(рис.18). рис.15
рис.15  рис.16
рис.16

 ; 2)
; 2)  .
.




 :
:  .
.

 .
. рис.19
рис.19 получается из графика функции
получается из графика функции  сдвигом вдоль оси Oy на
сдвигом вдоль оси Oy на  единиц (вверх, если
единиц (вверх, если  , и вниз, если
, и вниз, если  ).
). получается из графика функции
получается из графика функции  единиц (вправо, если
единиц (вправо, если  , и влево, если
, и влево, если  ).
). получается из графика функции
получается из графика функции  раз), если
раз), если  (
(  ).
). получается из графика функции
получается из графика функции  раз), если
раз), если  (
(  ).
). получается из графика функции
получается из графика функции  получается из графика функции
получается из графика функции  получается из графика функции
получается из графика функции  получается из графика функции
получается из графика функции  .
. – отрезок (сегмент, замкнутый промежуток);
– отрезок (сегмент, замкнутый промежуток); – интервал (открытый промежуток);
– интервал (открытый промежуток); – полуоткрытые интервалы;
– полуоткрытые интервалы; ;
;  ;
; ;
;  ;
; R.
R. – окрестностью
– окрестностью  точки
точки  называется интервал
называется интервал  , где
, где  , то выполняется неравенство
, то выполняется неравенство 

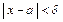 (рис.20а).
(рис.20а). , то неравенство
, то неравенство  определяет проколотую
определяет проколотую  точки
точки 

 называется бесконечно малой функцией (б.м.ф.) при
называется бесконечно малой функцией (б.м.ф.) при  , если для любого сколь угодно малого положительного числа
, если для любого сколь угодно малого положительного числа  существует положительное число
существует положительное число  такое, что для всех x из проколотой
такое, что для всех x из проколотой  .
. .
.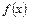 в точке
в точке  является бесконечно малой функцией при
является бесконечно малой функцией при  , где
, где  – б.м.ф. при
– б.м.ф. при  .
. , т.е.
, т.е.  .
. , где
, где  .
. найдется такая
найдется такая 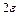 , ограниченной прямыми
, ограниченной прямыми  и
и  (рис.21).
(рис.21). рис.21
рис.21 имеют пределы при
имеют пределы при  . Тогда:
. Тогда: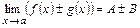 .
. число.
число. .
. .
. ,
, 
 – сложная функция, то
– сложная функция, то  .
. . Бесконечно большие функции
. Бесконечно большие функции . Число А называется пределом функции
. Число А называется пределом функции  , если для любого сколь угодно малого положительного числа
, если для любого сколь угодно малого положительного числа  , что при
, что при , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  .
.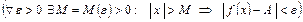 .
. существует такое число
существует такое число  , что для что для всех x из проколотой
, что для что для всех x из проколотой  .
.

 – б.б.ф. при
– б.б.ф. при  .
. , что для что для всех x, удовлетворяющих неравенству
, что для что для всех x, удовлетворяющих неравенству  .
.

 – б.б.ф. при
– б.б.ф. при  и б.м.ф. при
и б.м.ф. при  , т.е. при
, т.е. при 
 и
и  . При
. При 
 и
и  .
. – б.б.ф. при
– б.б.ф. при  .
. ), то функция
), то функция  – бесконечно большая при
– бесконечно большая при  – бесконечно малая при
– бесконечно малая при  ;
; .
. ; 2)
; 2)  ; 3)
; 3)  .
. .
. при
при  является бесконечно малой величиной, тогда по теореме о связи бесконечно малой и бесконечно большой функциями получим
является бесконечно малой величиной, тогда по теореме о связи бесконечно малой и бесконечно большой функциями получим .
. при
при  .
. .
. .
. ,
,  ,
,  ,
, 
 ,
,  ,
,  .
. с неопределенностью вида
с неопределенностью вида  и
и  – многочлены степени n и m соответственно.
– многочлены степени n и m соответственно.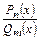 , т.е.
, т.е.  , то
, то  ;
; , то
, то  ;
; , то
, то  , где
, где  и
и  – старшие коэффициенты многочленов
– старшие коэффициенты многочленов  и
и  соответственно.
соответственно. .
. . Вынося за скобку и в числителе и в знаменателе
. Вынося за скобку и в числителе и в знаменателе 
 .
.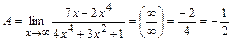 .
. .
. .
. . Вынося за скобку и в числителе и в знаменателе
. Вынося за скобку и в числителе и в знаменателе  .
. ,
,  ), тогда по правилу 2 получим
), тогда по правилу 2 получим .
. .
. . Вынося за скобку и в числителе и в знаменателе
. Вынося за скобку и в числителе и в знаменателе 
 .
. ,
,  ), тогда по правилу 2 получим
), тогда по правилу 2 получим .
. .
. . Чтобы выяснить, какова наибольшая степень среди слагаемых дроби, следует сначала вынести
. Чтобы выяснить, какова наибольшая степень среди слагаемых дроби, следует сначала вынести 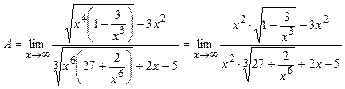 .
. , получим
, получим
 .
. .
. .
. с неопределенностью вида
с неопределенностью вида  неопределенность устраняется. Правило можно применять неоднократно.
неопределенность устраняется. Правило можно применять неоднократно. , где
, где  – многочлен степени n-1, полученный делением «уголком» многочлена
– многочлен степени n-1, полученный делением «уголком» многочлена  . Также многочлен можно разложить на множители методом группировки слагаемых. Если квадратный трехчлен
. Также многочлен можно разложить на множители методом группировки слагаемых. Если квадратный трехчлен  имеет корни
имеет корни  и
и  , то разложение этого трехчлена на множители примет вид
, то разложение этого трехчлена на множители примет вид  .
. .
. и
и  . Разложив числитель и знаменатель дроби на множители, получим
. Разложив числитель и знаменатель дроби на множители, получим
 .
. .
. .
. и
и  .
.
 .
. с неопределенностью вида
с неопределенностью вида  сопряженный множитель имеет вид
сопряженный множитель имеет вид  , при этом
, при этом  . Для иррациональности
. Для иррациональности  сопряженным является множитель
сопряженным является множитель  , при этом
, при этом  .
. .
. . Тогда
. Тогда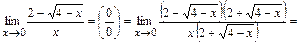
 .
. .
. .
. и
и  . Тогда
. Тогда

 .
. .
. .
. . Тогда
. Тогда
 .
. .
.