
|
|
Способ 3 (матричный метод — с помощью обратной матрицы).Экзаменационная программа. [1] –учебник (Письменный Д.Т., Конспект лекций по высшей математике: полный курс, М.: Айрис-пресс, 2006) [2] –сборник задач (Сборник задач по высшей математике. 1 курс и 2 курс; К.Н.Лунгу, Д.Т.Письменный, С.Н.Федин, Ю.А.Шевченко, М.: Айрис-пресс, 2007)
1. Первообразная. Определение. Теорема о разности двух первообразных (доказательство, ее геометрический смысл) ( [1], Глава VII, §29(29.1), теорема 29.1). 2. Неопределенный интеграл. Определение. Основные свойства (с доказательством) ( [1], Глава VII, §29(29.1, 29.2) ). 3. Интегрирование по частям в неопределенном интеграле (вывод формулы, примеры ее применения) ( [1], Глава VII, §30(30.3), примеры 30.6, 30.7 и 30.9; см. также [2], том 1, задачи 8.2.20, 8.2.30 ). 4. Интегрирование рациональных дробей разложением на простейшие слагаемые: простейшие дроби 1-го и 2-ого и 3-ого типа. Метод неопределенных коэффициентов (на конкретных примерах) ( [1], Глава VII, §31(31.1–текст после теоремы 31.7), (31.3), примеры 31.4,31.5 и 29.2 из §29; [2], том 1, задача 8.3.12.а)). 5. Определенный интеграл как предел интегральных сумм. Геометрический смысл определенного интеграла. Условия существования определенного интеграла (без доказательства), ( [1] Глава VII, §35, §36. См. также [2], том 1, пример 9.1.26 ). 6. Линейность определенного интеграла (с док). 7. Аддитивность определенного интеграла (с док). 8. Определенный интеграл от неравенства (с док). 9. Теорема об оценке определенного интеграла (с док). 10.Теорема о среднем для определенного интеграла(с док) 11.Формула Ньютона - Лейбница (с доказательством) ( [1], Глава VII, §37,теорема 37.1; лекции; §39(39.1) ) . 12.Дифференциальные уравнения 1-го порядка. Основные понятия; примеры. Постановка задачи Коши для уравнения 1-го порядка. ( [1], Глава X, §48(48.1); §49(49.1), пример 48.4; см. также теоремы 48.1 и 49.1 и [2], том 1, задачу 2.1.22 ). 13.Дифференциальные уравнения 2-го порядка. Основные понятия; примеры. Постановка задачи Коши для уравнения 2-го порядка. ( [1], Глава X, §48(48.1); §49(49.1), пример 48.4; см. также теоремы 48.1 и 49.1 и [2], том 1, задачу 2.1.22 ). 14. 15. Линейные дифференциальные уравнения 2-го порядка. Линейная зависимость и независимость решений. Структура общего решения линейного однородного дифференциального уравнения 2-го порядка (без доказательства) ( [1], Глава X, §49(49.4), теоремы 49.2,49.3,49.4,49.5 ). 16. Линейные неоднородные дифференциальные уравнения 2-го порядка. Структура общего решения линейного неоднородного дифференциального уравнения 2-го порядка (без доказательства) ( [1], Глава X, §51 (51.1); теорема 51.1; формула (51.4) ). 17. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Вывод формулы для общего решения в случае действительных различных корней характеристического уравнения (положительный дискриминант) ( [1], Глава X, §50 (50.1–случай 1, формула (50.3); пример50.1 ). 18. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Вывод формулы для общего решения в случае действительных одинаковых корней характеристического уравнения (нулевой дискриминант) ( [1], Глава X, §50 (50.1–случай 2, формула (50.4) ). 19.Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Вывод формулы для общего решения в случае комплексно-сопряженных корней характеристического уравнения (отрицательный дискриминант)
Задачи
[1] –учебник (Письменный Д.Т., Конспект лекций по высшей математике: полный курс, М.: Айрис-пресс, 2006) [2] –сборник задач (Сборник задач по высшей математике. 1 курс и 2 курс; К.Н.Лунгу, Д.Т.Письменный, С.Н.Федин, Ю.А.Шевченко, М.: Айрис-пресс, 2007)
II. Вычислить интегралы: а) Решение: а) Согласно методу подведения под знак дифференциала
б) Здесь используется метод интегрирования по частям
в) Имеем интеграл от рациональной дроби.
г) Воспользуемся формулой Ньютона-Лейбница:
Решить типичные задачи: а) а) а) а) а) а) а) a) Примеры решения аналогичных задач есть в [1]: примеры 29.1, 29.2,30.1,30.6, 30.7, 30.9,31.4, 31.5 и в [2], том 1: задачи 8.1.1, 8.1.5,8.1.8,8.1.15, 8.1.22, 8.2.1, 8.2.10, 8.3.12 а), 9.1.12, 9.1.46, 9.1.52, 9.1.59, 9.1.61. См. также задачи 8.2.15, 8.2.20, 8.2.27, 8.2.30,8.3.1. __________________________________________________________________________________
III. Решить дифференциальные уравнения и задачу Коши: 1. Решение: Нужно разделить переменные и проинтегрировать:
Окончательно получим Заметим, что ответ можно преобразовать:
2. Решение: Мы имеем дело с задачей Коши для линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами. Сначала найдем общее решение уравнения. Составим характеристическое уравнение Решением задачи Коши является функция Окончательно, 3. Решение: Данное дифференциальное уравнение является линейным неоднородным уравнением второго порядка с постоянными коэффициентами и правой частью специального вида. Общее решение линейного неоднородного уравнения 2-го порядка состоит из суммы общего решения соответствующего линейного однородного уравнения и частного решения неоднородного уравнения, т.е. общее решение неоднородного уравнения дается формулой:
Чтобы найти общее решение линейного однородного уравнения, составим характеристическое уравнение Частное решение неоднородного уравнения ищем методом неопределенных коэффициентов. Так как Окончательно имеем Решить типичные задачи: 1. 1. 1. 1. 1. 1. 1. 1. Примеры решения аналогичных задач есть в [1]: примеры 49.5, 50.1, 50.2, см. также 51.4,51.2,51.3. Аналогичные задачи с решениями есть в [2], том 2: задачи 2.7.18, 2.7.25, 2.7.30 , 2.7.37, 2.7.43. __________________________________________________________________________________ IV. 1. Даны координаты вершин пирамиды Найти: а) длину ребра б) угол между векторами в) площадь грани г) объём пирамиды Решение: а) Найдем координаты вектора
б) Найдем координаты вектора Из пункта а)
в) Найдем координаты вектора
Площадь грани равна половине длины вектора
г) Объём пирамиды
Здесь использовались свойства определителей. Можно было провести другое вычисление:
Окончательно имеем Решить типичные задачи: Даны координаты вершин пирамиды 1) 2) 3) 4) Найти: а) длину ребра б) угол между векторами в) объём пирамиды Даны координаты вершин пирамиды 1) 2) 3) 4) Найти: а) длину ребра б) угол между векторами в) площадь грани Аналогичные задачи с решениями есть в [2], том 1: задачи 3.1.13, 3.2.8 а), 3.3.5, см. также 3.4.4. __________________________________________________________________________________ V. Решить систему линейных уравнений и сделать проверку
Решение: Способ 1 (метод Гаусса). Выпишем расширенную матрицу этой системы линейных уравнений и преобразуем ее следующим образом:
Таким образом, мы имеем:
Проверка: Подставим полученное решение в исходную систему, тогда имеем
Способ 2 (метод Крамера). Вычислим четыре определителя этой системы:
Далее находим
Способ 3 (матричный метод — с помощью обратной матрицы). Представим систему линейных уравнений
тогда Найдем 1) 3) 5)
Решить типичные задачи:
Решить систему линейных уравнений и сделать проверку 1) 4) 7)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , б)
, б)  , в)
, в)  , г)
, г)  .
. ;
;
 ;
; , т.к. согласно теории интегрирования правильных рациональных дробей,
, т.к. согласно теории интегрирования правильных рациональных дробей, . Здесь A и B мы нашли следующим образом:
. Здесь A и B мы нашли следующим образом: .
.
 .
. , б)
, б)  , в)
, в) 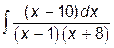 , г)
, г) 
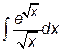 , б)
, б)  , в)
, в)  , г)
, г) 
 , б)
, б)  , в)
, в)  , г)
, г) 
 , б)
, б)  , в)
, в)  , г)
, г) 
 , б)
, б)  , в)
, в)  , г)
, г) 
 , б)
, б)  , в)
, в)  , г)
, г) 
 , б)
, б)  , в)
, в)  , г)
, г)  а)
а)  , б)
, б)  , в)
, в)  , г)
, г) 
 a)
a) 


 .
.
 ;
; . Так как корни характеристического уравнения
. Так как корни характеристического уравнения  , то общее решение однородного уравнения имеет вид
, то общее решение однородного уравнения имеет вид  .
. , где
, где  – действительные числа, которые нужно найти из начальных условий. Для этого возьмем производную
– действительные числа, которые нужно найти из начальных условий. Для этого возьмем производную  , подставим в
, подставим в  и
и  начальные условия
начальные условия  и решим получившуюся систему
и решим получившуюся систему 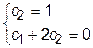 . Тогда
. Тогда  .
. – решение задачи Коши.
– решение задачи Коши.
 .
. и найдем его корни
и найдем его корни  . Получили случай действительных различных корней характеристического уравнения. Следовательно, общее решение однородного уравнения:
. Получили случай действительных различных корней характеристического уравнения. Следовательно, общее решение однородного уравнения:  .
. и
и  , то частное решение имеет вид:
, то частное решение имеет вид:  . Для функции
. Для функции  . Подставим
. Подставим  в исходное неоднородное уравнение и получим равенство для определения неопределенного коэффициента
в исходное неоднородное уравнение и получим равенство для определения неопределенного коэффициента  :
:  , откуда
, откуда  , а
, а  .
. – общее решение линейного неоднородного уравнения.
– общее решение линейного неоднородного уравнения. ; 2.
; 2.  ; 3.
; 3. 
 ; 2.
; 2.  ; 3.
; 3.  .
. ; 2.
; 2.  ; 3.
; 3. 
 ; 2.
; 2. 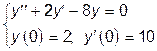 ; 3.
; 3. 
 ; 2.
; 2.  ; 3.
; 3. 
 ; 2.
; 2.  ; 3.
; 3. 
 ; 2.
; 2.  ; 3.
; 3. 
 ; 2.
; 2.  ; 3.
; 3.  .
. ,
,  ,
,  и
и 
 ;
; и
и  ;
; ;
; .
. , тогда длина ребра
, тогда длина ребра  ;
; и его длину
и его длину  .
. и
и  , поэтому
, поэтому
 . Тогда векторное произведение векторов
. Тогда векторное произведение векторов равно
равно .
. :
:
 .
. . Находим смешанное произведение:
. Находим смешанное произведение:
 .
. .
. .
. ,
,  ,
,  и
и  .
. ,
,  ,
, 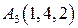 и
и  .
. ,
, 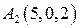 ,
,  и
и  .
. ,
,  ,
,  и
и  .
. ,
,  ,
,  и
и  .
. ,
,  и
и  .
. ,
,  ,
,  и
и  .
. ,
,  ,
,  и
и  .
.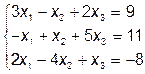

 , то есть
, то есть  .
. — верно!
— верно!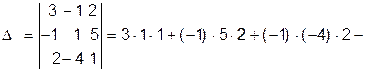






 ,
,  ,
,  .
. или
или  ,
, .
. , для этого вычислим:
, для этого вычислим: , 2)
, 2) 
 4)
4) 

 2)
2)  3)
3) 
 5)
5)  6)
6) 
 8)
8) 