
|
|
ГРАДИЕНТ ФУНКЦИИ. ПРОИЗВОДНАЯ ПО НАПРВЛЕНИЮ.ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ.
Рассмотрим функцию:
Th.1 Пусть : 1. g(x) определена в 2. g(x) дифференцируема в точке 3. Тогда
Доказательство: а) пусть n=1. g(x) дифференцируема в точке
Пусть
Т.к.
=
б) n>1. Это частный случай пункта а), т.к. рассматриваемая функция
Выпишем формулу (1) для всех частных случаев: n=1, k=2:
ПРИМЕР.
n=2, k=2:
Пусть
ПРИМЕР.
Замечание 1. Пусть сложная функция вида
При определенных условиях эта сложная функция является сложной функцией своих аргументов При этом частные производные указанной сложной функции по аргументам
Эти формулы обозначим за В.
Замечание 2. Частный случай, когда функции А зависят от одного аргумента t. Тогда мы имеем сложную функцию одной переменной t:
Производная
df.1 Пусть
Доказательство формулы следует из Th.1 при Th.2 (Инвариантность формы записи первого дифференциала) Пусть y=g(x) – дифференцируема в точке 1. Сложная функция y=g(x(t))=F(t) – дифференцируема в точке 2. ЗАМЕЧАНИЕ. Пусть функция f(x), Он будет функцией 2n переменных фиксированных а) б) в) Докажем б). Из Th о дифференцируемости сложной функции следует, что функция U(x)V(x) дифференцируема, если дифференцируемы U(x) и V(x). Далее имеем: = ПРИМЕР. Найти дифференциал функции Решение. Пусть
ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ. Пусть дана функция Пусть теперь для Аналогично. Частной производной порядка
Частная производная, полученная дифференцированием по различным переменным, называется смешанной. Например: Пусть Частные производные по x и y от функций
Аналогично определяются частные производные более высокого порядка. Для функции
ПРИМЕР.
Имеем: В этом примере смешанные частные производные равны друг другу. Вообще говоря, значения смешанных производных зависит от порядка, в котором производится последовательные дифференцирования. Нетрудно заметить, что число частных производных с увеличением порядка возрастает. Однако, некоторые из них при наличии условий совпадают. Th.1 Пусть Пусть смешанные частные производные m-го порядка непрерывны в точке Тогда смешанные частные производные порядка ”m” не зависят от порядка дифференцирования. (Б/Д). Следует отметить, что это условие достаточное. Перефразируем Th.1 для случая функции двух переменных. n=2 m=1: Пусть df.1 Пусть ПРИМЕР.
ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ. Пусть Рассмотрим дифференциал:
df.1 Вторым дифференциалом (дифференциалом второго порядка) 1. 2. При вычислении дифференциалов от На основании этого определения получается формула (2):
где Формулу (2) можно записать в более компактном виде. Введем следующие понятия. Символ Аналогично определяется оператор Определим степени и производные степеней операторов
При действии его на функцию
Символ При действии этого оператора на функцию
Определим
При действии оператора Формулу (2) запишем в операторном виде:
Дифференциал
df.2 Дифференциалом порядка “m” функции f в точке называется дифференциал от дифференциала порядка “m-1” при тех же предположениях, что и в предыдущем определении. Th.2 Пусть функция
СЛЕДСТВИЕ. (n=2) Пусть
(Б/Д). В частности если функция
Применим формулу
Поэтому
В силу непрерывности смешанных производных Если в некоторой области G функция U имеет непрерывные частные производные третьего порядка, то при фиксированных Из (2) легко найдем
По методу математической индукции легко убедиться, что (при фиксированных
Дадим сокращенную символическую запись дифференциалов высших порядков. Для этого в выражении 1-ого дифференциала условно «вынесем букву U за скобки» Если в выражении Аналогично можно записать символический третий дифференциал:
Вообще при
Правую часть следует понимать так же, как и в равенстве (4). Двучлен, стоящий в скобках, формально возводится по формуле бинома Ньютона в Формулу (5) легко обобщить и на случай функции При выполнении соответствующих условий будем иметь:
ЗАМЕЧАНИЕ. Если ввести формально дифференциальный оператор:
то выражение для дифференциалов можно записать в удобной символической форме:
Под произведением дифференциальных операторов понимается их последовательное применение. Например, если
ЗАМЕЧАНИЕ. Для дифференциалов высших порядков инвариантность формы записи не сохраняется. Th.3 (Формула Тейлора) Пусть функция
Следует иметь ввиду Если n=2
+
Следует иметь ввиду:
ГРАДИЕНТ ФУНКЦИИ. ПРОИЗВОДНАЯ ПО НАПРВЛЕНИЮ. df,1 Пусть
Пусть Тогда
Частные производные, определенные нами ранее, можно назвать производными в направлении координатных осей. Поставим вопрос о производных по любому фиксированному направлению. 1) Рассмотрим функцию f(x,y,z) определенную в 2) Дан вектор 3) z L ● ●
Пусть df.1 Обозначение: Пусть Th.1 Пусть f(x,y,z) дифференцируема в точке Доказательство: Очевидно,
Рассмотрим функцию = Но из (1) следует Можно записать так:
Следует отметить, что Формальные свойства градиента: 1) 2) 3) 4) df.2 Плоскость
Такая плоскость для дифференцируемой в точке (1) (2) Уравнение (2) единственно, т.к. представление (1) для дифференцируемой функции единственно. При этом нормальный вектор плоскости (3) т.е. геометрический смысл дифференциала – приращение аппликаты, касательной к графику функции, при переходе от точки df.3 Нормалью к поверхности в точке
Рассмотрим поверхность, заданную уравнением F(x,y,z,)=0 (5) (где F имеет непрерывные частные производные), то считая z неявной функцией x и y и дифференцируя это равенство по x и по y, получим:
Т.е. за нормальный вектор можно взять:
Уравнение плоскости касательной в точке
Следовательно, что уравнение нормали (т.е. перпендикуляра к касательной плоскости в точке
Формулы (6)и (7)имеют силу лишь для неособых (ординарных) точек поверхности. Точка Можно показать, что в достаточно малой окрестности неособой точки уравнение F(x,y,z)=0 однозначно разрешимо относительно одной из координат, причем это решение имеет непрерывные частные производные.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , функция f(t) определена в
, функция f(t) определена в  , где
, где  .
. (т.е.
(т.е.  ).
).
 :
: (1)
(1)
 ,
,  . Причем
. Причем .
. при
при 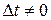 :
: (*)
(*) непрерывна в точке
непрерывна в точке  при
при . Кроме того
. Кроме того 
 переходим к пределу в (*)при
переходим к пределу в (*)при  :
:
 т.е. имеем y=g(x).
т.е. имеем y=g(x). , т.к.
, т.к.  ч. и т. д.
ч. и т. д.

 .
. 




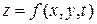 , где
, где 




 .
. где
где А
А .
. и через частные производные функции Апо следующим формулам:
и через частные производные функции Апо следующим формулам:




 этой сложной функции определяется формулой:
этой сложной функции определяется формулой:
 ,
, и удовлетворяет условиям Th.1 в точке
и удовлетворяет условиям Th.1 в точке  . Тогда
. Тогда 
 - полная производная.
- полная производная. . При
. При  .
. - дифференцируема в точке
- дифференцируема в точке  .
. (Б/Д).
(Б/Д).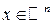 дифференцируема во всех точках некоторого открытого множества
дифференцируема во всех точках некоторого открытого множества  . Тогда в каждой точке
. Тогда в каждой точке  можно вычислить дифференциал:
можно вычислить дифференциал:  .
. причем при
причем при дифференциал есть линейная функция
дифференциал есть линейная функция  . Правила дифференцирования такие же, как и для функции одной переменной.
. Правила дифференцирования такие же, как и для функции одной переменной.

 , если
, если  .
. =
= .
. .
. , тогда:
, тогда:
 . Определенные ранее частные производные
. Определенные ранее частные производные  называют также частными производными первого порядка.
называют также частными производными первого порядка. -ет частная производная по
-ет частная производная по  в точке
в точке  . Тогда
. Тогда  называют частными производными второго порядка.
называют частными производными второго порядка. называется частная производная (по любой переменной
называется частная производная (по любой переменной  .
.
 и т.д.
и т.д. , т.е.
, т.е.  - определена в некоторой области E.
- определена в некоторой области E.  - также являются функциями двух переменных и определены в области E или ее части.
- также являются функциями двух переменных и определены в области E или ее части.

 , f определена в области E, z=f(x,y) –частные производные третьего порядка определяются формулами:
, f определена в области E, z=f(x,y) –частные производные третьего порядка определяются формулами:
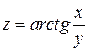 .
.
 ,
,  ,
,  ,
,  .
.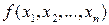 определена вместе со своими частными производными в окрестности
определена вместе со своими частными производными в окрестности  до порядка ”m”.
до порядка ”m”. определены в точке
определены в точке  непрерывны в точке
непрерывны в точке  . Тогда, частные производные
. Тогда, частные производные 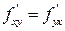 . (Б/Д).
. (Б/Д). .
. .
.

 .
. и
и  (дифференцируема в окрестности точки
(дифференцируема в окрестности точки  )
)  ,
,  .
. - это дифференциал первого порядка. (1)
- это дифференциал первого порядка. (1) функции
функции  в (.)
в (.)  определяется как дифференциал в (.)
определяется как дифференциал в (.)  от дифференциала первого порядка
от дифференциала первого порядка  при следующих условиях:
при следующих условиях: (при вычислении дифференциала от
(при вычислении дифференциала от  как постоянные множители).
как постоянные множители). приращения независимых переменных
приращения независимых переменных  ,
, .
. будем называть оператором частной производной по переменной
будем называть оператором частной производной по переменной  . При действии этого оператора на функцию
. При действии этого оператора на функцию  получается новая функция – частная производная
получается новая функция – частная производная  .
. частной производной по
частной производной по  .
. следующим образом:
следующим образом: оператор второй частной производной по
оператор второй частной производной по  получится
получится  .
. оператор смешанной второй производной по
оператор смешанной второй производной по  оператор смешанной производной
оператор смешанной производной  го порядка
го порядка  раз по
раз по  раз по
раз по  назовем оператором дифференциала.
назовем оператором дифференциала.
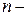 ю степень оператора дифференциала как
ю степень оператора дифференциала как 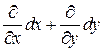 . В частности, при
. В частности, при  , получаем:
, получаем:
 на функцию
на функцию 
 произвольного
произвольного  , при выполнении всех условий, ранее сформулированных.
, при выполнении всех условий, ранее сформулированных. в операторной форме.
в операторной форме. , тогда
, тогда  :
: (Б/Д).
(Б/Д). , тогда
, тогда 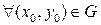 :
: , где
, где 
 имеет непрерывные частные производные до второго порядка включительно, то, воспользовавшись теоремой о равенстве смешанных производных, получаем:
имеет непрерывные частные производные до второго порядка включительно, то, воспользовавшись теоремой о равенстве смешанных производных, получаем:

 (1) к
(1) к  получаем:
получаем:



 они равны и поэтому
они равны и поэтому  (2)
(2) .
.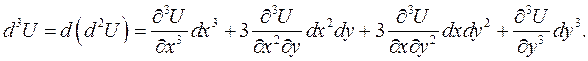 (3)
(3) ого порядка справедлива формула:
ого порядка справедлива формула:

 (формально в скобках в раскрытом виде квадрат двучлена)
(формально в скобках в раскрытом виде квадрат двучлена)  (4). Правую часть этой формулы следует понимать как двучлен, стоящий в скобках, формально следует возвести в квадрат и результат умножить на U, причем U следует поставить рядом с
(4). Правую часть этой формулы следует понимать как двучлен, стоящий в скобках, формально следует возвести в квадрат и результат умножить на U, причем U следует поставить рядом с  .
.
 будем иметь символическое равенство:
будем иметь символическое равенство: (5)
(5) число переменных.
число переменных.
 (1)
(1)
 , то
, то
 (2)
(2) ; При применении дифференциальных операторов вида (1) нужно пользоваться правилом (2). При этом дифференциалы независимых переменных
; При применении дифференциальных операторов вида (1) нужно пользоваться правилом (2). При этом дифференциалы независимых переменных 
 Справедлива формула Тейлора:
Справедлива формула Тейлора:
 , где
, где  .
.
 . (Б/Д).
. (Б/Д). , тогда
, тогда  справедлива формула Тейлора:
справедлива формула Тейлора:
 .
. . Если
. Если  - в форме Пеано.
- в форме Пеано. , где
, где .
. (дифференцируема в точке
(дифференцируема в точке  . Рассмотрим прямоугольную декартовую систему координат с базисом
. Рассмотрим прямоугольную декартовую систему координат с базисом  . Тогда вектор, координаты которого имеют вид:
. Тогда вектор, координаты которого имеют вид: - называется градиентом функции f в токе
- называется градиентом функции f в токе 
 - ортонормированный базис прямоугольной декартовой системы координат.
- ортонормированный базис прямоугольной декартовой системы координат. . Часто используют символическую запись, вводя, векторный оператор Гамильтона (гамильтонян или набла).
. Часто используют символическую запись, вводя, векторный оператор Гамильтона (гамильтонян или набла). , тогда
, тогда  (т.е. произведение числа на вектор
(т.е. произведение числа на вектор  ).
). .
. .
.
 .
.



 y
y , L – прямая,
, L – прямая,  ,
,  -некоторый вектор.
-некоторый вектор. , если он существует
, если он существует  называется производной f(x,y,z) в точке
называется производной f(x,y,z) в точке 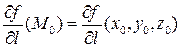 .
. - единичный вектор.
- единичный вектор.  - направляющие вектора, косинусы вектора
- направляющие вектора, косинусы вектора  и
и  .
. , с другой стороны
, с другой стороны  , тогда:
, тогда:
 , f(x,y,z) удовлетворяет теореме о производной сложной функции. Тогда,
, f(x,y,z) удовлетворяет теореме о производной сложной функции. Тогда,  =
= .
. , т.е.
, т.е.  =
=  (2)
(2) (3)
(3) не зависит от выбора системы координат. Можно показать, что наличие производных по любому направлению не является достаточным условием дифференцируемости функции f(x,y,z). Из (3) также следует, независимость
не зависит от выбора системы координат. Можно показать, что наличие производных по любому направлению не является достаточным условием дифференцируемости функции f(x,y,z). Из (3) также следует, независимость  от выбора системы координат (т.к.
от выбора системы координат (т.к.  - угол между
- угол между  достигает максимума при
достигает максимума при  (т.е.
(т.е.  ) т.е. при совпадении направления
) т.е. при совпадении направления  . Таким образом, для дифференцируемой функции
. Таким образом, для дифференцируемой функции  ;
; ;
; ;
; .
. называется касательной к поверхности z=f(x,y) в точке
называется касательной к поверхности z=f(x,y) в точке  ,
, 

 .
. ,
, 
 касательная плоскость имеет вид:
касательная плоскость имеет вид:
 из уравнения (2).
из уравнения (2).
 .
. (4)
(4)

 (6)
(6) (7)
(7) не обращаются в нуль.
не обращаются в нуль.