
|
|
Часть 2. Циклоидальный маятникЛабораторная работа № 19 ИССЛЕДОВАНИЕ КОЛЕБАНИЙ МАТЕМАТИЧЕСКОГО И ЦИКЛОИДАЛЬНОГО МАЯТНИКОВ Цель работы: исследование зависимости периода колебаний математического и циклоидального маятников маятника от амплитуды. Приборы и оборудование: ПК с установленными программами виртуальных маятников. Литература: Полное описание лабораторной работы находится на рабочем столе ПК. Савельев И. В. Курс общей физики. Т. 1. Механика Молекулярная физика. - М.: Наука, 1982. Бать М. И., Джанелидзе Г. Ю., Кельзон А. С.. Теоретическая механика в примерах и задачах. В 3-х т. Т. 2. Динамика. – М.: Наука, 1991. Кудрявцев П. С. Курс истории физики. – М.: Просвещение, 1982. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. В 3-х т. – СпБ.: Лань. 1997. Введение Часть 1. Математический маятник Рассмотрим задачу о нахождении закона колебаний математического маятника, длина нити которого равна L.
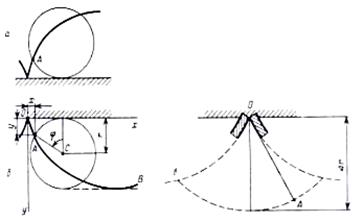
Математическим маятником (см. рис. 19.1) называется материальная точка, подвешенная посредством невесомой нерастяжимой нити к неподвижной оси и движущаяся в вертикальной плоскости. В начальный момент маятнику, нить которого занимала отвесное положение, была сообщена посредством толчка начальная угловая скорость w0. На рисунке маятник изображен в отклоненном положении от вертикали на угол j. Направление положительного отсчета угла поворота j указано на рисунке. Маятник совершает качания около оси Z, перпендикулярной к плоскости рисунка и проходящей через точку привеса O. Траекторией материальной точки является дуга окружности, расположенная в вертикальной плоскости с центром в О и радиусом L. Напишем для маятника уравнение вращательного движения
Изображаем силу тяжести материальной точки Р= Mg и реакцию нити Т. Момент натяжения нити R относительно оси Z равен нулю, а момент силы тяжести Р равен
Учитывая знаки проекций, и что момент инерции маятника равен J = mL2, приведем уравнение (19.3) к виду
Малые колебания Решение нелинейного дифференциального уравнения колебаний маятника (19.3) представляет известные трудности. Поэтому решим задачу приближенно, считая колебания маятника малыми. Разложив sin j в ряд
и пренебрегая членами разложения порядка выше первого, получим sinj » j. Тогда дифференциальное уравнение (19.3) принимает вид:
Обозначив
Решения этого линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами ищем в виде
Корни характеристического уравнения равны Общее решение уравнения представляет собой функцию
Используя функцию Эйлера
Постоянные интегрирования определим из начальных условий: в начальный момент маятнику, нить которого занимала отвесное положение, была сообщена посредством толчка начальная угловая скорость, то есть при t=0 имеем j0=0 и w=w0. Дифференцируя по времени, выражение для j (23.7), находим
Подставив в (19.7) t=0 и j=0, а в (23.8) t=0 и w=0 получим C1=0 и С2=(dj/dt)/w. Теперь уравнение (19.7) можно записать так
здесь
Итак, маятник совершает гармонические колебания с угловой амплитудой a и с частотой Период колебаний маятника равен
Масса материальной точки не входит в выражение периода колебаний Т. Следовательно, материальные точки с различными массами имеют при одинаковой длине нити маятника L один и тот же период колебаний. Замечание. В секундном маятнике Т/2 = 1 с, или Произвольные колебания Поставим задачу определить период колебаний T математического маятника без ограничения sinj»j. Задача вновь приводит к решению дифференциального уравнения
Обозначим
получим
Проинтегрировав, последнее соотношение находим
Учитывая начальные условия: при j=a
или
Воспользуемся тригонометрическим тождеством
получим
Сделаем подстановку
Приходим к выражению:
Теперь уравнение (19.10) принимает вид
или
В силу начального условия: при t=0 j=0, из формулы (19.10) вытекает, что в начальный момент y=0, а из условия: при t=T/4 j=a следует, что y=p/2. Поэтому
где
где
является эллиптическим интегралом первого рода. Разложим в ряд
получаем
Этот ряд сходится равномерно относительно φ, ибо мажорируется при всех значениях φ сходящимся рядом
следовательно, получим почленным интегрированием
После подстановки значения k в формулу (10) приходим к искомому выражению периода колебаний маятника:
то есть колебания маятника при конечной угловой амплитуде a свойством изохронности не обладают — его период зависит от угловой амплитуды колебаний a. Считая a малой величиной и пренебрегая в формуле (19.13) членами разложения, содержащими a во второй и более степенях, получим приближенную формулу (19.9):
При угловой амплитуде колебаний a=20° период колебаний, подсчитанный по формуле (11) или по более точной формуле (19.13), больше периода колебаний маятника, определенного по приближенной формуле (19.9), всего лишь на 0,8%, но при a=60° – соответственно уже на 3,5%. Часть 2. Циклоидальный маятник Циклоидальным называется маятник, который может быть представлен как материальная точка, движущаяся по дуге циклоиды.
Покажем, что колебания циклоидального маятника, в отличие от колебаний математического, обладают свойством изохронности, то есть его период колебаний не зависит от начальных условий движения. Представление о циклоиде связано, например, с траекторией точки А лежащей на ободе колеса, которое катится без скольжения по прямолинейному рельсу (рис.19.2а). На рис. 19.2 б изображено колесо, массой которого по сравнению с массой точки А, укрепленной на его ободе, можно пренебречь. Колесо катится по рельсу, расположенному над ним. Покажем, что движение точки А является колебательным около нижней точки В циклоиды, причем период этих колебаний не зависит от начальных условий движения. Выберем в качестве обобщенной координаты угол j образуемый радиусом АС точки А с вертикалью. Уравнение циклоиды в параметрическом виде имеет вид
где r- радиус колеса. Уравнение Лагранжа для маятника таково:
Единственной активной силой, действующей на маятник, является сила тяжести материальной точки, которую мы обозначим Р. Потенциальная энергия U материальной точки выражается формулой:
В свою очередь, обобщенная сила Q может быть записана так:
Внося в эту формулу выражение (19.16), имеем
Вычислим кинетическую энергию Т материальной точки:
Формула (19.14) позволяет найти проекции скоростей на оси координат
Выражение для энергии примет вид формула (5) принимает вид
Вычислим частную производную кинетической энергии Т по обобщенной скорости
и по времени от полученной производной:
Найдем теперь частную производную выражения (19.18) кинетической энергии Т по обобщенной координате j
Подставив выражения для производных в уравнение Лагранжа (19.15), получим
Вводя тригонометрические функции половинных, углов и сокращая на sin(j)/2, имеем
Нетрудно видеть, что
Следовательно, дифференциальное уравнение (19.22) можно записать так:
Наконец, обозначив cos(j/2) = z, приходим к уравнению
где k2=g/4r. Таким образом, точное дифференциальное уравнение (19.23) колебаний циклоидального маятника аналогично приближенному дифференциальному уравнению (19.6) колебаний математического маятника:
Это значит, что колебания циклоидального маятника обладают свойством полной изохронности, т.е. период его колебаний не зависит от начальных условий движения. Воспользовавшись формулой (19.9), можно записать период колебаний в виде
где Эволюта циклоиды (геометрическое место центров кривизны) также является циклоидой, тождественной исходной. Поэтому для осуществления рассматриваемого маятника следует вырезать шаблон, изображающий два участка дуг циклоиды, примыкающие к ее точке возврата О (рис. в). Нить длиной Измерения Выполнение работы начинается нажатием кнопки "Эксперимент", которая открывает программу-эксперимент, являющуюся самостоятельным приложением и может работать независимо от главного окна. Переход между основной программой и экспериментом осуществляется стандартными средствами переключения приложений используемыми в операционной системе Windows (например, при помощи "Панели задач" или сочетания клавиш Alt+Tab). Задание 1 Построить графики зависимостей периода колебаний математического маятника от длины нити, массы груза и амплитуды. Для уменьшения погрешности измерения периода, число колебаний следует брать достаточно большим, не меньше 50. Измерения проводить не менее чем для 10 случаев возможных изменений параметров. Задание 2 По полученным данным выяснить характер зависимости периода колебаний от параметров маятника (длины нити и массы) и начальных условий (амплитуды). Это можно сделать при помощи численных методов или экспортировав результаты в Microsoft Exсel, воспользоваться уже реализованными методами, то есть добавить линию тренда, аппроксимировав какой либо из предложенных Exсel-ем зависимостей. Задание 3 Проанализировать полученные результаты, проверить их соответствие данным, полученным при помощи теоретических выкладок. Объяснить возможные расхождения. Задание 4 Проделать задания 1, 2 и 3 для случая циклоидального маятника. Положение маятника в этом случае задает параметр t из уравнения циклоиды, и интервал по модулю от 0° до 180°. Задание 5 Сравнить результаты, полученные при исследованиях математического и циклоидального маятников. Ответить на контрольные вопросы. Отчет о поделанной работе принимается как в письменном, так и в электронном виде. Более подробные сведения о работе с экспериментальной программой можно получить из встроенной в нее справочной системы.
Контрольные вопросы 1. Что называют математическим маятником? 2. Что называют циклоидальным маятником? 3. Получите уравнение циклоиды. 4. Дайте определение основным характеристикам колебательного движения: амплитуда, период, частота, фаза. 5. Что такое изохронность? 6. Что называют свободными колебаниями? 7. Получите дифференциальное уравнение колебаний математического маятника. 8. Получите приближенную формулу для периода колебаний математического маятника. 9. Какая система называется несвободной? 10. Что такое механическая связь? 11. Дайте определение идеальной связи? 12. Запишите общее уравнение динамики вращательного движения твердого тела.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 . Итак, модуль суммарного момента сил, приложенных к маятнику, равен
. Итак, модуль суммарного момента сил, приложенных к маятнику, равен .
. ,
,
 .
. , запишем окончательно:
, запишем окончательно: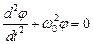 .
. . Подстановка j в уравнение (19.6) приводит к характеристическому уравнению
. Подстановка j в уравнение (19.6) приводит к характеристическому уравнению .
. .
. .
. выражению можно придать вид:
выражению можно придать вид: .
. .
.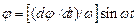 ,
, . Обозначим
. Обозначим  ; тогда окончательно имеем
; тогда окончательно имеем .
. .
. , т. е. длина нити секундного маятника равна приблизительно равна 1 м.
, т. е. длина нити секундного маятника равна приблизительно равна 1 м. .
.
 ,
,
 .
. , имеем
, имеем  и, следовательно,
и, следовательно,
 .
.
 .
. .
.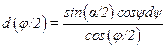 .
.

 ,
,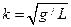 . Итак, период колебаний маятника равен
. Итак, период колебаний маятника равен ,
,
 Полагая
Полагая


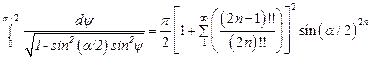

 ,
,
 ,
, .
.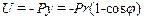 .
. .
. .
. .
. .
. .
.

 .
.
 .
.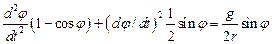 .
.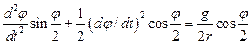 .
.
 .
. ,
,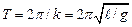 ,
, .
.