Вычисление частотных характеристик

Для вычисления частотных характеристик при помощи программы «Статистика 6.0» необходимо воспользоваться командой «Frequency tables» (с анг. яз., «таблица частот») в модуле «Basic statistics/Tables» («Основная статистика и таблицы»).

Пример задачи: Исследователь должен определить процентное соотношение респондентов, ответивших «да», «нет» и «не знаю» на следующий вопрос: «Считаете ли Вы уместным запретить любую рекламу табачной продукции на территории России?». Также, необходимо узнать, сколько мужчин и женщин из группы респондентов ответили положительно на данный вопрос.

Решение: После проведения подготовительных работ с документом (см. Приложение 4) он будет выглядеть следующим образом:

Необходимо отметить, что в таблице не допускается оставление пустых ячеек в столбце выбранной переменной.

В первом столбце «0» обозначает респондента женского пола, «1» - мужского.

Выберите «Statistics» («Статистика») > «Basic statistics/Tables» («Основные статистики и таблицы») > «Frequency tables» («Таблица частот»):

В открывшемся диалоговом окне «Frequency tables» нажмите на «Variables», выберите строчку «2-ответы», после чего нажмите «ОК».

Далее нажмите на функцию «Options» («Настройки») и оставьте «галочку» только напротив «Percentages» («Проценты»):

Нажмите на «Summary» («Вывод»):

В колонке «Count» («Итог») показано число респондентов, в колонке «Percent» - их процентное соотношение. В нашем примере ответили «Да» («а») 40% респондентов, «Нет» («b») – 28%, «Не знаю» («с») – 32%.

Чтобы ответить, сколько мужчин и женщин из группы респондентов ответили положительно на вопрос исследователя, необходимо в диалоговом окне «Frequency tables» нажать на кнопку «Select cases» («Выбор испытуемых»):

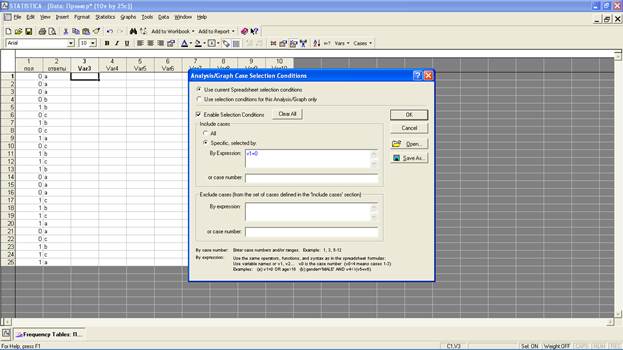
В открывшемся диалоговом окне «Analysis/Graph Case Selection Conditions» («Условия выбора испытуемых») в строчке «By Expression» («Проявление») функции «Include cases» («Выбранные испытуемые») впишите формулу v1=0, которая показывает, что при обработке программа выберет в столбце v1 респондентов только с обозначением «0», то есть женского пола:

Далее нажмите на «OK»:

В нашем примере 58,3% (7 человек) респондентов женского пола положительно ответили на вопрос исследователя.

Если в строчке «By Expression» функции «Include cases» вписать формулу v1=1, то в итоге программа подсчитает число и процентное соотношение ответов у мужчин:

В нашем примере только 23% (3 человека) респондентов мужского пола положительно ответили на вопрос исследователя.

Факторный анализ

Факторный анализ – статистический метод, который используется при обработке больших массивов экспериментальных данных. Задачами факторного анализа являются: сокращение числа переменных (редукция данных) и определение структуры взаимосвязей между переменными, т.е. классификация переменных, поэтому факторный анализ используется как метод сокращения данных или как метод структурной классификации [2].

Важное отличие факторного анализа от описанных выше методов заключается в том, что его нельзя применять для обработки первичных, или, как говорят, «сырых», экспериментальных данных, т.е. полученных непосредственно при обследовании испытуемых. Материалом для факторного анализа служат корреляционные связи, а точнее – коэффициенты корреляции Пирсона, которые вычисляются между переменными (т.е. психологическими признаками), включенными в обследование.

Главное понятие факторного анализа – фактор.Это искусственный статистический показатель, возникающий в результате специальных преобразований таблицы коэффициентов корреляции между изучаемыми психологическими признаками, или матрицы интеркорреляций. Процедура извлечения факторов из матрицы интеркорреляций называется факторизацией матрицы. В результате факторизации из корреляционной матрицы может быть извлечено разное количество факторов вплоть до числа, равного количеству исходных переменных. Однако факторы, выделяемые в результате факторизации, как правило, неравноценны по своему значению [1, 3].

Элементы факторной матрицы называются «факторными нагрузками, или весами»;и они представляют собой коэффициенты корреляции данного фактора со всеми показателями, использованными в исследовании.

Факторная матрица показывает, какие переменные образуют каждый фактор. Это связано, прежде всего, с уровнем значимости факторного веса. По традиции минимальный уровень значимости коэффициентов корреляции в факторном анализе берется равным 0,4 или даже 0,3 (по абсолютной величине), поскольку нет специальных таблиц, по которым можно было бы определить критические значения для уровня значимости в факторной матрице. Следовательно, самый простой способ увидеть, какие переменные «принадлежат» фактору - это значит отметить те из них, которые имеют нагрузки выше, чем 0,4 (или меньше чем - 0,4). В некоторых компьютерных пакетах иногда уровень значимости факторного веса определяется самой программой и устанавливается на более высоком уровне, например 0,7.

Перед факторизацией необходимо провести процедуру вращение факторов, которая изменяет положение факторов по отношению к переменным таким образом, что получаемое решение легко интерпретировать. Цель вращения – преобразовать факторную матрицу таким образом, чтобы получилась простая структура, в которой каждый фактор имеет некоторое количество больших нагрузок и некоторое маленьких, и подобно этому каждая переменная имеет существенные нагрузки только по некоторым факторам.

Как показывает практика, психологи предпочитают использовать метод варимакс [2]. При использовании данного метода минимизируется количество переменных, имеющих высокие нагрузки на данный фактор, при этом максимально увеличивается дисперсия фактора. Это способствует упрощению описания фактора за счет группировки вокруг него только тех переменных, которые в большей степени связаны с ним, чем остальные.

Разработано несколько приемов для выбора «правильного» числа факторов из корреляционной матрицы. Определение числа выделяемых факторов, вероятно, наиболее важное решение, которое необходимо принять при проведении факторного анализа. Неверное решение может привести к бессмысленным результатам при обработке самого четкого набора данных. Нет ничего страшного в том, чтобы попытаться выполнить несколько вариантов анализа, базирующегося на разном числе факторов, и использовать нескольких различных приемов, определяющих выбор факторов.

Первые руководящие принципы — это теория, здравый смысл, а также прошлый опыт. При этом психолог должен установить:

· не способствует ли увеличение числа факторов уменьшению доли нагрузок в диапазоне от -0,4 до +0,4? Если это так, то это увеличение, скорее всего, не имеет смысла;

· не появляются ли какие-либо большие корреляции между факторами при осуществлении вращений.

· не разделились ли какие-либо хорошо известные факторы на две или большее количество частей.

Факторный анализ может быть уместен, если выполняются следующие условия.

1. Нельзя факторизовать качественные данные, полученные по шкале наименований, например, такие, как цвет волос (черный / каштановый / рыжий) и т.п.

2. Все переменные должны быть независимыми, а их распределение должно приближаться к нормальному.

3. Связи между переменными должны быть приблизительно линейны или, по крайней мере, не иметь явно криволинейного характера.

4. В исходной корреляционной матрице должно быть несколько корреляций по модулю выше 0,3. В противном случае достаточно трудно извлечь из матрицы какие-либо факторы.

5. Выборка испытуемых должна быть достаточно большой. Рекомендации экспертов варьируют. Наиболее жесткая точка зрения рекомендует не применять факторный анализ, если число испытуемых меньше 100, поскольку стандартные ошибки корреляции в этом случае окажутся слишком велики. Однако если факторы хорошо определены (например, с нагрузками 0,7, а не 0,3), экспериментатору нужна меньшая выборка, чтобы выделить их. Кроме того, если известно, что полученные данные отличаются высокой надежностью (например, используются валидные тесты), то можно анализировать данные и по меньшему числу испытуемых.

Пример задачи: необходимо выделить два фактора из шести имеющихся переменных: рост, вес, размер ноги курсанта, его отметки за вступительный экзамен по биологии и истории, а также средний балл за сессию.

Решение: После проведения подготовительных работ с документом (см. Приложение 5) он будет выглядеть следующим образом:

Выберите «Statistics» («Статистика») > «Multivariate Exploratory Techniques» («Многомерные разведочные технологии») > «Factor Analysis» («Факторный анализ»):

В открывшемся диалоговом окне «Factor Analysis» нажмите кнопку «Variables» и выберите колонки с требуемыми переменными, в нашем примере это шесть позиций:

После чего нажмите «ОК» и еще раз «ОК»:

По умолчанию в строчке «Maximum no. of factors» («Максимальное количество факторов» установлено два выделяемых фактора. Нажимаете «ОК»:

В строчке «Factor rotation» («Вращение фактора») установите «Varimax raw» («Варимакс сырых данных»). В строчке «Highlight factor loading greater than» («Факторная нагрузка больше, чем») установите минимально допустимое значение – 0,4:

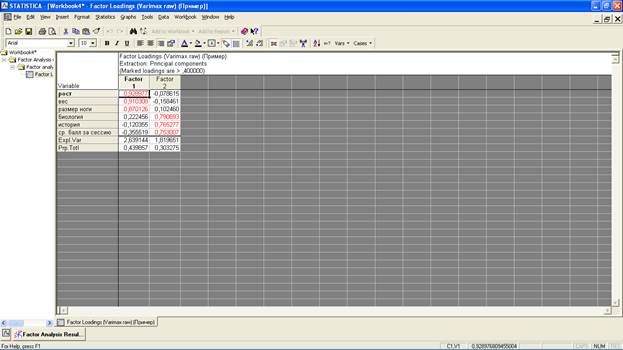
Нажмите на «Summary»:

В нашем примере мы выявили два очевидных фактора, которые условно можно назвать «Конституция (телосложение)» и «Успеваемость». В фактор «Конституция» вошли такие переменные, как «рост», «вес» и «размер ноги». В фактор «Успеваемость» - «биология», «история» и «средний балл за сессию». Стоит отметить, что у всех переменных факторная нагрузка оказалось выше 0,7, что свидетельствует о их весомой статистической принадлежности соответствующему фактору.

Регрессионный анализ

Регрессионный анализ позволяет предсказать, чему в среднем будет равно значение одного признака при заданном значении другого признака.

Достаточно часто связь между двумя психологическими признаками имеет линейный характер:

у = a + bx, где

· y и x - анализируемые признаки;

· а - свободный член уравнения; при b = 0 получаем y = а, т.е. а - это точка, в которой линия регрессии пересекается с осью
OY (эту точку называют также «j-пересечением», или
«Intercept»);

· b - коэффициент регрессии, отражающий угол наклона
линии регрессии. Чем больше b отличается от 0, тем сильнее
связь между анализируемыми признаками.

Даже если связь между психологическими признаками носит нелинейный характер (например, экспоненциальный), практически всегда можно выделить участки, хорошо аппроксимируемые линейной регрессией.

Приведенное выше уравнение можно использовать для описания связи между двумя признаками лишь при выполнении следующих обязательных условий:

· зависимость между признаками носит линейный характер;

· оба признака распределены нормально.

Пример задачи: Исследователь должен определить коэффициенты линейного регрессионного уравнения, описывающего связь между показателями систолического давления и нервно-психической устойчивостью (НПУ) испытуемых.

Решение: Расчет коэффициентов регрессионных уравнений можно выполнить в нескольких модулях программы Statistica 6.0. Мы воспользуемся модулем Multiple Regression Analysis
(Анализ множественной регрессии).

В появившемся окне нажмите на кнопку Variables и укажите, какая из анализируемых переменных является зависимой (Dependent variable), а какая - независимой (Independent variable) (в нашем примере систолическое давление зависит от НПУ).

Нажмите на кнопку «ОК».

В итоге появится окно, которое уже на данном этапе анализа содержит некоторые важные его результаты:

а) Dependent: имя зависимой переменной;

б) No. of cases: число наблюдений;

в) Intercept: значение свободного члена регрессионного уравнения;

г) Std. error: стандартная ошибка свободного члена регрессионного уравнения;

д) Multiple R: коэффициент множественной корреляции;

е) R: коэффициент детерминации. Это очень важный показатель в регрессионном анализе. Он изменяется от 0 до 1 и отражает «качество» рассчитанной регрессии, показывая долю (%) общего разброса выборочных точек, которая «объясняется» построенной регрессией (например, при R² = 0,85, следует вывод о том, что 85% дисперсии зависимой переменной y объясняется вариацией независимой переменной х);

ж) Adjusted R²: скорректированный на число степеней свободы коэффициент детерминации (Adjusted R-square = 1 - (1 - R-square)x[n/(n - p)], где n - число наблюдений, р - число независимых переменных плюс 1);

з) Standard error of estimate: параметр, отражающий степень разброса выборочных значений относительно линии регрессии;

и) F, dfиp: F-критерий, число степеней свободы, принятое при его расчете, и вероятность ошибки для нулевой гипотезы F-теста. F-тест в регрессионном анализе применяется для оценки статистической значимости модели. При p<0,05 можно заключить, что рассчитанная регрессия удовлетворительно описывает связь между исследуемыми признаками;

к) t(df) и p: критерий Стьюдента t используется для проверки нулевой гипотезы о равенстве 0 свободного члена регрессионного уравнения. Р - вероятность ошибки для этой нулевой гипотезы;

л) beta: стандартизованный коэффициент регрессии - это коэффициент регрессии, который мы получили бы в случае предварительной стандартизации обеих переменных (т.е. при таком преобразовании, когда их средние значения стали бы равны 0, а стандартные отклонения - 1). Расчет beta позволяет оценить, в какой степени значения зависимой переменной определяются значениями независимой переменной. Beta может оказаться особенно полезным показателем при включении в анализ нескольких независимых переменных, выражающихся в разных единицах измерения - в таком случае коэффициент отражал бы удельный вклад каждой из этих переменных в вариацию зависимой переменной. При наличии одной независимой переменной коэффициент beta идентичен Multiple R.

Нажмите кнопку «Summary: Regression results»(Результаты регрессионного анализа). Появится таблица с результатами анализа, в которой:

а) Beta: стандартизованный коэффициент регрессии;

б) Std. err. of beta: стандартная ошибка стандартизованного коэффициента регрессии;

в) В: один из самых важных столбцов в этой таблице, поскольку именно он содержит искомые значения свободного члена регрессионного уравнения (в строке Intercept) и коэффициента регрессии (нижняя строка таблицы);

г) Std. err. of B: стандартные ошибки коэффициентов уравнения;

д) t(df): значения t-критерия Стьюдента, который используется для проверки гипотезы о равенстве обоих коэффициентов уравнения 0;

е) p-level: вероятность ошибки для нулевой гипотезы о равенстве коэффициентов уравнения нулю.

Из итоговой таблица видно, что оба коэффициента регрессии статистически значимо отличаются от 0 (p < 0,05) и что в целом построенная регрессионная модель отлично описывает связь между систолическим давлением и нервно-психической устойчивостью. Само же рассчитанное уравнение мы можем записать следующим образом:

Н= 2,682 x А + 33,289, где Н - давление, А – нервно-психическая устойчивость человека.

Важной частью регрессионного анализа является анализ остатков (остатки представляют собой разности между наблюдаемыми значениями зависимой переменной и теми ее значениями, которые предсказываются регрессионной моделью). Он запускается путем нажатия кнопки «Perform residual analysis» (Выполнить анализ остатков) на закладке «Residuals /Assumptions /Predictions» (Остатки / Условия / Предсказания).

Первое, что нужно проверить в отношении остатков - это нормальностьих распределения. Для этого на закладке «Quick»подмодуля анализа остатков нажмите кнопку «Normal plot of residuals», чтобы построить график нормальных вероятностей. Если точки на этом графике достаточно тесно укладываются вдоль теоретически ожидаемой прямой, то можно заключить, что остатки распределяются нормально. Иначе линейная регрессионная модель для анализируемых переменных будет неприменима.

Второе условие в отношении остатков состоит в том, что их дисперсия должна оставаться неизменной во всем диапазоне значений анализируемых переменных. Для проверки этого условия на закладке «Scatterplots» (Диаграммы рассеяния) нажмите кнопку «Predicted vs. Residuals», чтобы построить график зависимости значений остатков от предсказываемых моделью значений зависимой переменной. Если проверяемое условие выполняется, то точки на этом графике будут располагаться хаотично, не проявляя никакой закономерности. Если же в расположении точек имеется тенденция (разброс увеличивается слева направо, точки тесно укладываются вдоль прямой, и т.п.), линейный регрессионный анализ также неприменим.

В рассмотренном примере оба условия в отношении остатков выполняются, что еще раз подтверждает адекватность рассчитанной регрессионной модели для описания связи между артериальным давлением и нервно-психической устойчивостью.

ЛИТЕРАТУРА

1) Дружинин В.Н. Экспериментальная психология. - СПб.: Питер, 2011.

2) Ермолаев О.Ю. Математическая статистика для психологов: Учебник. - М.: МПСИ, Флинта, 2011.

3) Корнилова Т.В. Экспериментальная психология: Теория и методы. - М.: Юрайт-Издат, 2012.

4) Куликов Л.В. Психологическое исследование: методические рекомендации по проведению. – СПб.: Речь, 2001. - с.90-92.

5) Практикум по общей, экспериментальной и прикладной психологии /Под ред. А.А.Крылова, С.А.Маничева. - СПб.: Питер, 2007.

6) Сидоренко Е.В. Методы математической обработки в психологии. – СПб.: ООО «Речь», 2000. – 350 с.

7) Худяков А. И. Экспериментальная психология в схемах и комментариях. – СПб.: Питер, 2008.

Приложение 1

Таблица 1

Значения критерия t_st для отбраковки выпадающих вариант

при разных уровнях значимости (p).

Таблица 2

Значение функции f(o_i)

(ординаты нормальной кривой)

Примечание. Значения вероятности p даны числами после запятой.

Таблица 3

Критические значения критерия c² для уровней статистической значимости р£0,05 и р£0,01 при разном числе степеней свободы V.

Различия между двумя распределениями могут считаться достоверными, если c²_эмп достигает или превышает c²_0,05, и тем более достоверными, если c²_эмп достигает или превышает c²_0,01 (по Большеву Л.Н., Смирнову Н.В., 1983).

Таблица 4

Значения критерия t Стьюдента при различных уровнях значимости (р)

Приложение 2

Таблица 1

Критические значения выборочного коэффициента корреляции рангов R_s Спирмена

Таблица 2

Критические значения коэффициента корреляции r_xy Пирсона

Не нашли, что искали? Воспользуйтесь поиском по сайту: