
|
|
Логические задачи в алгебре Жегалкина.
Рассмотрим снова первую задачу предыдущей главы. Напомним её: Задача 1. Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая удивительную находку, каждый высказал по два предложения: Алеша. Это сосуд греческий и изготовлен в 5 веке. Боря. Это сосуд финикийский и изготовлен в 3 веке. Гриша. Это сосуд не греческий и изготовлен в 4 веке.
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предложений.Где и в каком веке изготовлен сосуд?
Ранее было показано, что математическая модель данной задачи представляется следующей системой уравнений Булевой алгебры:
Также найдено решение этой системы: х1=0, х2=1, х3=0, х4=0, х5=1 (2) Система уравнений (1) отличается от уравнений линейной алгебры присутствием в ней неизвестных в инверсной форме. Чтобы избежать этого рассмотрим логическую операцию: сложение по модулю 2, которую иногда называют псевдоплюс и обозначают так: « Таблица 1:
Операция «сложение по модулю 2» примечательна тем, что она эквивалентна двум операциям двоичной арифметики - сложению и вычитанию двоичных чисел в одном разряде. Таблица 1 подтверждает справедливость следующего равенства
Вычислительным путем можно доказать, что
Эти вычисления представлены в таблицах 2 и 3. Таблица 2: Таблица 3:
Теперь с помощью формул (3) – (5) аналитическое выражение для логической функции
Здесь учтено дополнительно, что
При составлении новых алгебраических уравнений на базе такого представления логических функций следует иметь в виду то, что терм
Третье соотношение в системе (6) требует некоторых пояснений. Оно, как и другие, получено из равенства Система алгебраических уравнений (6) линейна и ее определитель имеет вид:
Так же как операция сложения по модулю два
где Если определитель
где
Определитель
Для этого: 1. Включите компьютер; 2. После того, как на экране монитора появится рабочий стол операционной системы Windows, откройте окно Microsoft Excel; 3. Заполните ячейки A1¸D4 таблицы элементами определителя D11; 4. активизируйте ячейку Е4, в которую запишите формулу =ОСТАТ(СУММ(B1*C2*D3;D1*B2*C3;C1*D2*B3;B1*D2*C3;C1*B2*D3;D1*C2*B3);2) – эта формула производит сложение по модулю 2 в приложении Microsoft Excel (см. рис. 14.1); 5. нажмите на клавишу Enter. Результат в ячейке будет равен 1. Аналогично вычисляем D15, разложением его по последней строке(
Рис. 14.2 Таким образом, оказывается что
в которых определитель 6. Занесем элементы матрицы А1 – в ячейки Н1¸L5; элементы матрицы А2 – в ячейки Н7¸L12; А3 – в ячейки Н14¸L18; А4 – в ячейки Н20¸L24; элементы матрицы А5 – в ячейки Н26¸L30; 7. Проведем элементарные преобразования над столбцами или строками матриц А2 А3 и А5 (А1 и А4 оставим без изменений, т.к. в них присутствуют строки, в которых все, кроме одного элемента, содержат нули (эти строки на рис. 3 выделены цветом). В результате в областях ячеек N7¸R12, N14¸R18, N26¸R30 получаем преобразованные матрицы А2 А3 и А5 соответственно, рис. 14.3.
8. В ячейке O5 запишем формулу нахождения х1:
в ячейке T13 – формулу для х2:
в ячейке T19 – формулу для х3:
в ячейке O24 – формулу для х4:
в ячейке T31 – формулу для х5:
Вычисление определителей в (8) по формуле (7) приводит к результатам: В действительности расчеты, приведшие к формулам (8), выполнены в, так называемой, алгебре Жегалкина. По определению алгебра Жегалкина – это множество Возникает естественный вопрос о том, что если формулы Крамера с определенными оговорками применимы для решения системы (6), то применимы ли другие методы обычной алгебры в данном случае. Для ответа на этот вопрос попытаемся использовать метод Гаусса для решения уравнений (6). Метод Гаусса решения систем линейных уравнений обычной алгебры состоит в том, что при помощи элементарных преобразований над строками расширенной матрицы системы её приводят к трапециевидной или треугольной матрице. Затем по трапециевидной матрице восстанавливают новый вид исходной системы уравнений, который позволяет легко найти решение. В обычной алгебре под элементарными преобразованиями матрицы подразумевают следующие операции: - умножение какой-либо строки матрицы на число, отличное от нуля; - прибавление к элементам одной строки матрицы соответствующих элементов другой, умноженных на одно и то же число; - перемена местами двух строк. Аналогичные операции выполняются и над столбцами. Так как алгебра Жегалкина определена на множестве чисел - прибавление к элементам одной строки матрицы соответствующих элементов другой; - перемена местами двух строк. Эти же элементарные преобразования справедливы и для столбцов. Система алгебраических уравнений (6) характеризуется двумя матрицами:
Здесь Над строками расширенной матрицы выполним следующие элементарные преобразования: 1) пятую и четвертую строки поменяем местами; 2) элементы первой строки прибавим к соответствующим элементам третьей и четвертой строк; 3) элементы второй строки прибавим к соответствующим элементам четвертой строки; 4) элементы четвертой строки прибавим к элементам пятой строки; 5) элементы третьей строки прибавим к элементам пятой строки; 6) третью и четвертую строки поменяем местами. Процесс упрощения матрицы Теперь к матрице, полученной после второго преобразования, применяем последовательно третье и четвертое преобразование: Наконец, применяем оставшиеся два преобразования(рис. 14.5):
Из проиллюстрированных этапов преобразования расширенной матрицы видно, что после последнего преобразования матрица
Теперь система (9) легко решается так называемым приемом снизу вверх. В результате чего будем иметь: Это решение совпадает с решением, полученным ранее по формулам Крамера, т.е. метод Гаусса применим и для систем линейных уравнений в алгебре Жегалкина. Для решения системы (6) с помощью обратной матрицы напомним некоторые понятия линейной алгебры. Определение. Пусть дана матрица
Вычеркнем в ней Определение. Пусть Если алгебраическое дополнение элемента
Очевидно, что в алгебре Жегалкина эту формулу следует переписать так:
причем при вычислении определителя Определение. Пусть дана квадратная матрица
в строках которой расположены алгебраические дополнения элементов соответствующих столбцов матрицы Определение. Квадратная матрица Теорема. Всякая невырожденная матрица В алгебре Жегалкина, если
В линейной алгебре стандартная форма записи n линейных уравнений с n неизвестными такова:
или в матричной форме
Здесь Решение уравнения (12) с помощью обратной матрицы записывается в виде
В алгебре Жегалкина коэффициенты Теперь решим систему (6) уравнений алгебры Жегалкина с помощью обратной матрицы. Для этого в соответствии с уравнением (12) перепишем её в матричном виде
Чтобы воспользоваться формулой (13) при нахождении решения уравнения (14), необходимо вычислить обратную матрицу. В данном случае, согласно соотношению (11) обратная матрица 9. 10. 11. Активизируйте ячейку L38 и запишите в неё формулу: =ОСТАТ(СУММ(J35*K36;K35*J36);2), после чего нажмите на клавишу Enter. Результат вычисления показан на рис. 6. После вычисления обратной матрицы уравнение (13) для системы (14) принимает следующий вид
Для получения
Рис. 14.7 После выполнения аналогичных вычислений для оставшихся неизвестных получаем: Таким образом, известные методы линейной алгебры с определенными оговорками применимы и для решения уравнений алгебры Жегалкина. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1)
(1)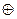 ». Правило для выполнения этой операции представлено в таблице 1.
». Правило для выполнения этой операции представлено в таблице 1.
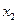

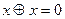 (3)
(3) , (4)
, (4)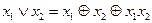 . (5)
. (5)

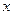

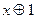
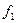 можно преобразовать так:
можно преобразовать так:
 и
и  . Выполнив аналогичные преобразования и над другими функциями, будем иметь
. Выполнив аналогичные преобразования и над другими функциями, будем иметь
 в
в  будет равным нулю, так как одно из входящих в него высказываний ложно. С учетом сказанного получаем следующую систему уравнений
будет равным нулю, так как одно из входящих в него высказываний ложно. С учетом сказанного получаем следующую систему уравнений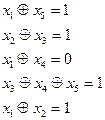 (6)
(6) . Но в этом равенстве, в отличие от других из (6), слева и справа стоит единица, которая по законам обычной алгебры сокращается. Так как к логическим равенствам Буль постулировал справедливость математической аксиомы о том, что равные количества, приложенные к равным, производят равные суммы, то указанное сокращение справедливо и в данном случае.
. Но в этом равенстве, в отличие от других из (6), слева и справа стоит единица, которая по законам обычной алгебры сокращается. Так как к логическим равенствам Буль постулировал справедливость математической аксиомы о том, что равные количества, приложенные к равным, производят равные суммы, то указанное сокращение справедливо и в данном случае.
 (7)
(7)
 - элемент i-ой строки и
- элемент i-ой строки и  - го столбца,
- го столбца, 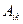 - алгебраическое дополнение
- алгебраическое дополнение  . При вычислении алгебраического дополнения
. При вычислении алгебраического дополнения 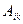 также учитывается, что операция сложения по модулю два эквивалентна операции сложения и вычитания двоичных чисел в одном разряде. Другими словами, здесь в отличие от обычной алгебры не обращается внимание на знак минус при выполнении арифметических операций.
также учитывается, что операция сложения по модулю два эквивалентна операции сложения и вычитания двоичных чисел в одном разряде. Другими словами, здесь в отличие от обычной алгебры не обращается внимание на знак минус при выполнении арифметических операций.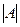 вычислять разложением по элементам его первой строки, то формула (7) принимает вид
вычислять разложением по элементам его первой строки, то формула (7) принимает вид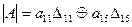 ,
,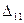 и
и  суть миноры элементов, стоящих в первом и пятом столбцах указанной строки. Так как
суть миноры элементов, стоящих в первом и пятом столбцах указанной строки. Так как 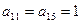 , то определитель
, то определитель 

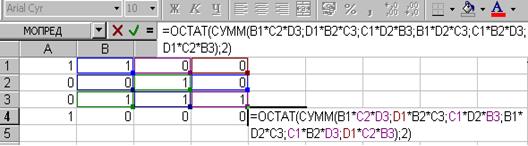 Рис. 14.1
Рис. 14.1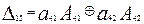 ). Формула вычисления и результат представлены на рис. 14.2.
). Формула вычисления и результат представлены на рис. 14.2.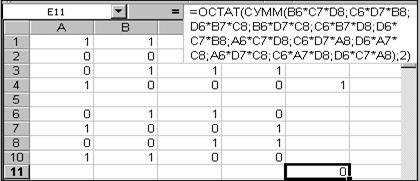
 , т.е. система (6) имеет единственное решение. Общеизвестные формулы Крамера в данном случае имеют вид:
, т.е. система (6) имеет единственное решение. Общеизвестные формулы Крамера в данном случае имеют вид: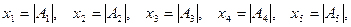 (8)
(8)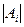 получается из определителя
получается из определителя 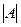 заменой i- того столбца столбцом свободных членов системы (6).
заменой i- того столбца столбцом свободных членов системы (6). Рис. 14.3
Рис. 14.3




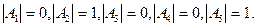 Таким образом, полученное решение (8) совпадает с решением (2), изложенным выше, но при этом расчеты по формуле (8) напоминают расчеты линейной алгебры.
Таким образом, полученное решение (8) совпадает с решением (2), изложенным выше, но при этом расчеты по формуле (8) напоминают расчеты линейной алгебры.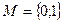 с заданными в нем операциями
с заданными в нем операциями  сложения по модулю два и конъюнкции. Соотношение (6) в данном случае представляет систему линейных алгебраических уравнений алгебры Жегалкина, и эта система представляет математическую модель рассматриваемой логической задачи.
сложения по модулю два и конъюнкции. Соотношение (6) в данном случае представляет систему линейных алгебраических уравнений алгебры Жегалкина, и эта система представляет математическую модель рассматриваемой логической задачи.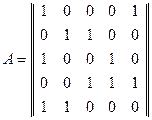
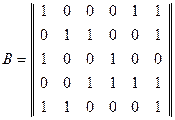
 - матрица коэффициентов системы, а
- матрица коэффициентов системы, а  - расширенная матрица системы, включающая столбец свободных членов системы (6).
- расширенная матрица системы, включающая столбец свободных членов системы (6).


 (9)
(9)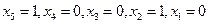 .
.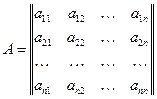
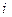 -ю строку и
-ю строку и  .
.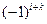 , называется алгебраическим дополнением этого элемента.
, называется алгебраическим дополнением этого элемента.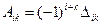
 , (10)
, (10)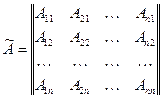 ,
, , то
, то  . Если
. Если 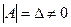 , то обратная матрица для
, то обратная матрица для 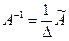 .
.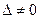 , то
, то  . Следовательно, обратная матрица определяется по формуле
. Следовательно, обратная матрица определяется по формуле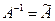 (11)
(11)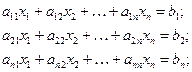
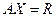 ; (12)
; (12)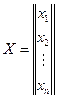 ;
; 
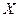 -столбец из неизвестных,
-столбец из неизвестных,  -столбец из свободных членов.
-столбец из свободных членов. (13)
(13)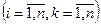 и свободные члены
и свободные члены 
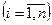 равны либо 0, либо 1; а знак сложения заменяется на знак сложения по модулю два. Формула (13) сохраняется с соблюдением операции умножения по правилам двоичной арифметики.
равны либо 0, либо 1; а знак сложения заменяется на знак сложения по модулю два. Формула (13) сохраняется с соблюдением операции умножения по правилам двоичной арифметики.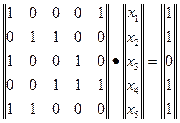 (14)
(14) состоит из следующих этапов:
состоит из следующих этапов: Занесем элементы дополнения А11 в ячейки Н34¸К37. Так как четвертая строка содержит все нули кроме первого элемента (на рис. 14.6 выделена цветом), то вычисление будем производить с элементами определителя, расположенного в ячейках I34¸K36.
Занесем элементы дополнения А11 в ячейки Н34¸К37. Так как четвертая строка содержит все нули кроме первого элемента (на рис. 14.6 выделена цветом), то вычисление будем производить с элементами определителя, расположенного в ячейках I34¸K36. В полученном определителе третьего порядка мы видим, что первая строка тоже содержит нули (кроме элемента I34=1), следовательно, вычисление дополнения А11 сводится к вычислению определителя второго порядка, расположенного в ячейках J35¸K36.
В полученном определителе третьего порядка мы видим, что первая строка тоже содержит нули (кроме элемента I34=1), следовательно, вычисление дополнения А11 сводится к вычислению определителя второго порядка, расположенного в ячейках J35¸K36.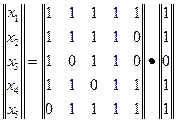 (15)
(15)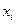 по (15) необходимо использовать известное в обычной алгебре правило умножения матрицы на столбец. Например,
по (15) необходимо использовать известное в обычной алгебре правило умножения матрицы на столбец. Например,  (см. рис. 14.7)
(см. рис. 14.7)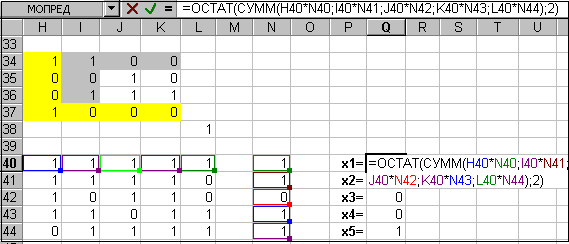
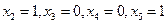 . Эти значения неизвестных означают, что сосуд финикийский и изготовлен в 5-ом веке.
. Эти значения неизвестных означают, что сосуд финикийский и изготовлен в 5-ом веке.