
|
|
Координаты центров тяжести однородных тел.12 Для однородного тела вес Подставив эти значения Р и
Как видно, центр тяжести однородного тела зависит только от его геометрической формы, а от величины Путем аналогичных рассуждений легко найти, что если тело представляет собой однородную плоскую и тонкую пластину, то для нее
где S - площадь всей пластины, a Точку, координаты которой определяются формулами называют центром тяжести площади S. Точно так же получаются формулы для координат центра тяжести линии:
где L — длина всей линии, l — длины ее частей. Таким образом, центр тяжести однородного тела определяется, как центр тяжести соответствующего объема, площади или линии.
Способы определения координат центра тяжести. Исходя из полученных выше общих формул, можно указать конкретные способы определения координат центров тяжести тел.
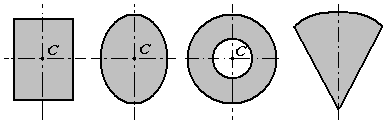
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии. 2. Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести и площадь известны.
3.Дополнение.Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.
Центры тяжести некоторых однородных тел. 1) Центр тяжести дуги окружности. Рассмотрим дугу АВ радиуса R с центральным углом
Рис.37 Найдем координату
где L - длина дуги АВ, равная
где угол 2) Центр тяжести площади треугольника. Разобьем площадь треугольника ABD (рис. 38) прямыми, параллельными AD, на узкие полоски; центры тяжести этих полосок будут лежать на медиане BE треугольника.
Рис.38
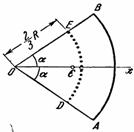
Следовательно, и центр тяжести всего треугольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке пересечения его медиан. При этом, как известно, 3) Центр тяжести площади кругового сектора. Рассмотрим круговой сектор ОАВ радиуса R с центральным углом
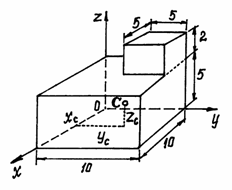
Рис.39 Пример 1. Определим центр тяжести однородного тела, изображённого на рис. 40.
Рис.40
Тело однородное, состоящее из двух частей, имеющих симметричную форму. Координаты центров тяжести их:
Объёмы их: Поэтому координаты центра тяжести тела
Пример 2. Найдем центр тяжести пластины, согнутой под прямым углом. Размеры – на чертеже (рис.41).
Рис.41
Координаты центров тяжести:
Площади: Поэтому:
Пример 3. У квадратного листа
Рис.42
В этой задаче удобнее разделить тело на две части: большой квадрат и квадратное отверстие. Только площадь отверстия надо считать отрицательной. Тогда координаты центра тяжести листа с отверстием:
координата Пример 4. Проволочная скобка (рис.43) состоит из трёх участков одинаковой длины l.
Рис.43
Координаты центров тяжести участков:

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
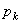 любой его части пропорционален объему
любой его части пропорционален объему 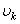 этой части:
этой части: 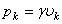 , а вес Р всего тела пропорционален объему V этого тела
, а вес Р всего тела пропорционален объему V этого тела 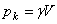 , где
, где 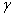 - вес единицы объема.
- вес единицы объема.

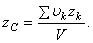
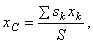

 - площади ее частей.
- площади ее частей.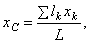



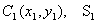
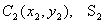
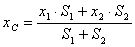
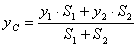
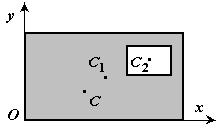
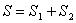 .
.

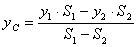
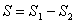 .
.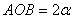 . В силу симметрии центр тяжести этой дуги лежит на оси Ox (рис. 37).
. В силу симметрии центр тяжести этой дуги лежит на оси Ox (рис. 37).
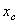 по формуле
по формуле  . Для этого выделим на дуге АВ элемент ММ’ длиною
. Для этого выделим на дуге АВ элемент ММ’ длиною 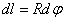 , положение которого определяется углом
, положение которого определяется углом 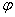 . Координата х элемента ММ’ будет
. Координата х элемента ММ’ будет  . Подставляя эти значения х и
. Подставляя эти значения х и 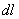 и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:
и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:
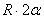 . Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном
. Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном
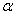 измеряется в радианах.
измеряется в радианах.

 (рис. 39). Разобьем мысленно площадь сектора ОАВ радиусами, проведенными из центра О, на п секторов. В пределе, при неограниченном увеличении числа
(рис. 39). Разобьем мысленно площадь сектора ОАВ радиусами, проведенными из центра О, на п секторов. В пределе, при неограниченном увеличении числа 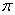 , эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DE радиуса
, эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DE радиуса 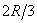 . Следовательно, центр тяжести сектора ОAB будет совпадать с центром тяжести дуги DE. Окончательно получим, что центр тяжести площади кругового сектора лежит на его центральной оси симметрии на расстоянии от начального центра О, равном
. Следовательно, центр тяжести сектора ОAB будет совпадать с центром тяжести дуги DE. Окончательно получим, что центр тяжести площади кругового сектора лежит на его центральной оси симметрии на расстоянии от начального центра О, равном 
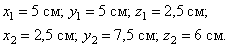
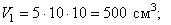
 .
.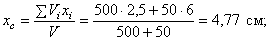
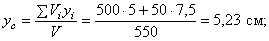
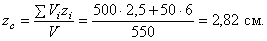

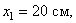
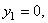


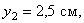
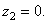
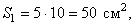

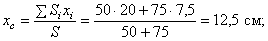
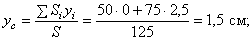
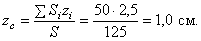
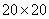 см вырезано квадратное отверстие
см вырезано квадратное отверстие 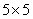 см (рис.42). Найдем центр тяжести листа.
см (рис.42). Найдем центр тяжести листа.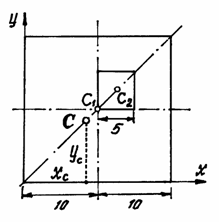
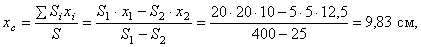
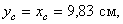 так как тело имеет ось симметрии (диагональ).
так как тело имеет ось симметрии (диагональ).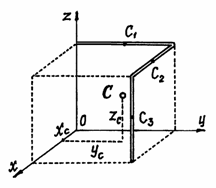
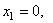
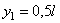 ,
, 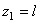 ;
; 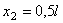 ,
, 
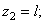
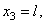
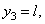
 Поэтому координаты центра тяжести всей скобки:
Поэтому координаты центра тяжести всей скобки: