
|
|
Метод Зейделя (итерационный метод)12 Цель; Дано; Условие на сходимость; Условие на точность- как в пред. Из уравнений выразить Итерационные формулы:
Начальные приближения:
М. Зейделя схож. с м. пр. интер. Ручной счет. Метод Зейделя Численно решить систему линейных уравнений
с точностью 0,1 Условие сходимости: переписать из примера итерации Итерационные формулы:
i=0 интер. 1
i=1 интер 2
Ответ: Решение задачи аппроксимации и интерполяции. Основные методы: -метод неопределенного коэффициента (интерполяция) -метод наименьшего квадрата (аппроксимация) Пусть имеется набор экспериментальных данных. Например, замеры силы тока в разные моменты времени. Введем обозначения: Х- аргумент (например, момент времени) Y- значение функции (например, сила тока) Х и Y являются исходными данными и известны заранее. Для 3 точек :
Задача аппроксимации и интерполяции заключается в нахождении аналитического выражения для функции y(x). (формулы) : Возможны 2 варианта : 1) y(x) проходит через исходные точки, что соответствует задаче интерполяции. Функция y(x) называется интерполирующий функцией. 2) y(x) проходит на наименьшем расстоянии от исходных точек, что соответствует задаче аппроксимации. Функция y(x) называется аппроксимирующий функцией. Функция y(x) находится как полином n-ой степени:
Интерполяция (метод неопределенного коэффициента) Интерполяция функция находится как полином степени n для исходных n+1 точек. Виды интерполяции: 1) n=1 - линейная;
2) n=2 - квадратичная, параболическая
3) n=3 - кубическая;
Метод неопределенных коэффициентов Цель: найти формулу для y(x) Дано: точки Условие на сходимость и на точность: нет Составить систему линейных уравнений: Кол-во уравнений: n+1 Кол-во неизвестных: n+1: Решаем систем, находим
Ручной счет. Метод неопределенного коэффициента Даны точки: Найти интегрирующие функции: а)кусочно-линейную б)параболическую Решение: (в лабе выбрать а) точки (-3; 4); (0; 1):
из (2): из (1):
точки (0; 1); (2; 5):
из (1): из (2):
Проверка:
Ответ:
б) точки (-3; 4); (0; 1); (2; 5)
{... решение методом Гаусса...}
Проверка:
Вершина параболы:
График:
Ответ: Аппроксимация (метод наименьшего квадрата) Аппроксимирующая функция находится как полином степени ниже или равной n для исходных n+1 точек. Виды аппроксимации: 1) n=1 (для
2) n=2 (для
и т.д. Метод наименьших квадратов Цель, дано, условие на сходимость, точность- также как в методе неопределенных коэффициентов Составить систему линейных уравнений: DA=F, где:
Решаем систему, находим Ручной счет. Метод наименьших квадратов Даны точки: Найти аппроксимирующие функции а) линейную б) параболическую Решение а)
Решаем систему, получаем
Значения y(x) в исх. точках:
Отклонения y(x) от исх. точек:
График:
Ответ: Б)
Значения y(x) в исходных точках:
Отклонения y(x) от исходных точек:
График:
Ответ: Лекция 4. Численное интегрирование. Основные методы: · Метод левых · Метод правых · Метод центральных · Метод трапеций · Метод Симпсона Пусть требуется вычислить определенный
Определенный интеграл Iравен площади фигуры между графиком f(x) и осью Х:
Для всех методов строится таблица:
Метод левых Цель: найти определенный интеграл Дано: Усл. сход, точн. – нет.
Опирается левым блоком. Метод правых
Опирается правым блоком. Метод центральных Опирается центром. Метод трапеций. Метод Симпсона. nдолжно быть четным! По нечетным точкам: I= 1, 3, … n – 1 По четным точкам: I = 2, 4, … n – 2
Ручной счет. Вычислить определенный интеграл
Расчет таблицы:
Метод левых
Метод правых
Метод центр.
Метод трапеций
Метод Симпсона По нечётным точкам: i = 1, 3 S По чётным точкам: i = 2 S
Решение ОДУ 2 порядка Дифференциальное уравнение – это уравнение, содержащее неизвестную функцию, производные неизвестной функции.
Решить ДУ – это значит найти неизвестную функцию y(x).
ДУ:
Порядком ДУ называется порядок наивысшей производной, входящей в уравнение.
Примеры:
Мы будем рассматривать ОДУ 2-го порядка: F(y Задача Коши – это задача о решении ОДУ с заданными начальными условиями. Решение ОДУ:
формула y(x)=cos(x)+3
таблица значений x, y:
Основные методы:
Постановка задачи.
Численно решить дифференциальное уравнениеF(y
Порядок решения:
Замена: y Выразить y Задача сведётся к виду:
Начальные условия:
Метод Эйлера простой.
Итерационные формулы:

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

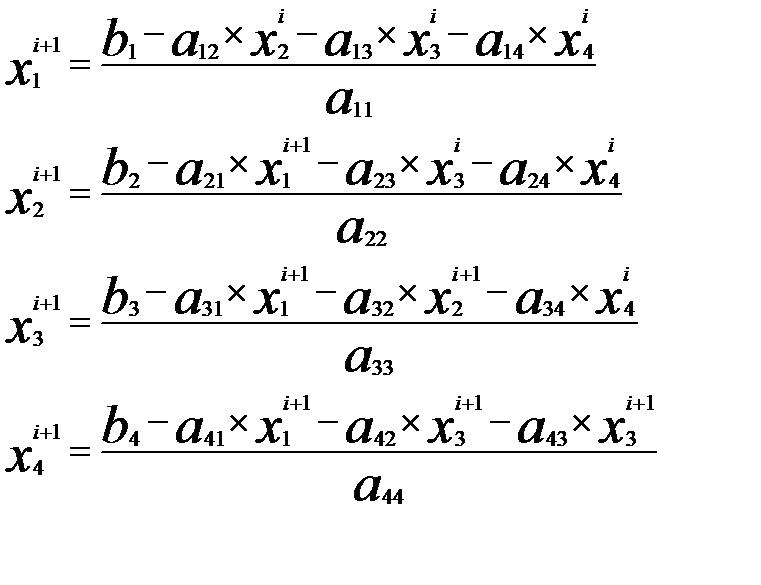

 на след. шаге вычисляется по старым
на след. шаге вычисляется по старым  и по новым
и по новым 






 - решение системы с точностью 0,1
- решение системы с точностью 0,1

 ,где
,где ,
,  ,
,  ,…,
,…,  -неизвестные коэффициенты, которые мы будем искать.
-неизвестные коэффициенты, которые мы будем искать. ; (для 2 точек)
; (для 2 точек)
 (для 3 точек)
(для 3 точек)
 (для 4 точек)
(для 4 точек)

 ,
,  ,
,  .
. для
для 

 ; подставляем их в y(x).
; подставляем их в y(x). ;
; 
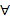 точки)
точки)




















 верно
верно верно
верно
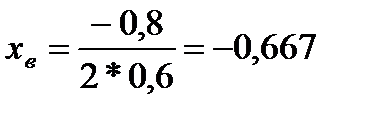


 точек)
точек)
 точек)
точек)



 ,..., подставляем в y(x)
,..., подставляем в y(x) ;
; 
 - искомая функция
- искомая функция
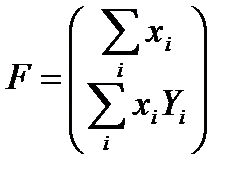



















 -Верно
-Верно
 – искомая функция.
– искомая функция.




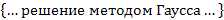













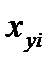















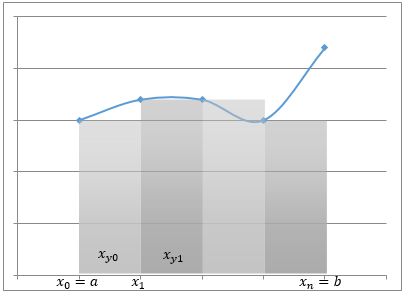





 с числом разбиений n= 4
с числом разбиений n= 4 














 = 0.25+2.25 = 2.5
= 0.25+2.25 = 2.5 = 1
= 1
 (обыкновенноедифференциальное уравнение1-го порядка)
(обыкновенноедифференциальное уравнение1-го порядка) (обыкновенноедифференциальное уравнение2-го порядка)
(обыкновенноедифференциальное уравнение2-го порядка) (обыкновенноедифференциальное уравнение2-го порядка)
(обыкновенноедифференциальное уравнение2-го порядка) (дифференциальное уравнение в частных произв. 2-го порядка)
(дифференциальное уравнение в частных произв. 2-го порядка) ,y
,y  ,y, x)=0
,y, x)=0
 на промежутке [a; b] с числом разброса п.
на промежутке [a; b] с числом разброса п. = z
= z из исх. уравнения.: y
из исх. уравнения.: y  =
= 
 (наша замена y
(наша замена y  … (выражение для у
… (выражение для у  )
)

 при i = 0, 1,…,n
при i = 0, 1,…,n