
|
|
Методические указания по решению задачи на тему «Построение закона распределения дискретной случайной величины»
Перед решением задачи убедитесь, что Вы знаете о: - дискретных случайных величинах; - формах задания закона распределения дискретной случайной величины; - математическом ожидании, дисперсии и среднем квадратичном отклонении случайной величины; - функции распределения случайной величины и вероятности попадания значений случайной величины в заданный интервал; - биномиальном законе распределения; - законе распределения Пуассона.
Рекомендуемая литература: 1 – 4.
Пример 4.4. Стрелок производит четыре выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. За каждое попадание стрелку насчитывается 5 очков. а) Построить ряд распределения числа полученных очков (случайная величина Х) по биномиальному закону. Проверить условие нормировки. б) Построить многоугольник распределения. в) Определить математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Х. Сделать выводы. г) Записать функцию распределения случайной величины Х, построить график функции. д) Найти вероятности того, что стрелок получит: - менее 10 очков; - от 5 до 15 очков; - более 10 очков.
Решение. а) Дискретная случайная величина Х – число полученных очков. Определим ее возможные значения: х1 = 0, если стрелок ни разу не попал в мишень; х2 = 5, если стрелок попал в мишень 1 раз; х3 = 10, если стрелок попал в мишень 2 раза; х4 = 15, если стрелок попал в мишень 3 раза; х5 = 20, если стрелок попал в мишень 4 раза. Чтобы построить ряд распределения, нужно определить вероятности, соответствующие каждому возможному значению случайной величины:
Для определения вероятностей используем формулу биномиального закона распределения (формулу Бернулли):
где n – количество независимых испытаний (4 выстрела, n = 4); р – вероятность события (попадания) в каждом из испытаний (р = 0,4); k – количество произошедших событий (попаданий); Сnk – число сочетаний из n элементов по k – неупорядоченные наборы по k элементов, взятых из n. Число сочетаний определяется по формуле:
Вероятность появления значения х1 соответствует вероятности того, что стрелок ни разу не попал в мишень (событие ни разу не произошло), вероятность появления значения х2 соответствует вероятности того, что стрелок попал в мишень 1 раз (событие произошло 1 раз) и т.д.:
Рассчитаем вероятности: k=0 Р4(0) = С40 * р0 * (1 – р)4-0
Р4(0) = 1 * 0,40 * 0,64 = 1 * 0,1296 = 0,1296
k = 1 Р4(1) = С41 * р1 * (1 – р)4-1
Р4(1) = 4 * 0,41 * 0,63 = 4 * 0,4 * 0,216 = 0,3456
k = 2 Р4(2) = С42 * р2 * (1 – р)4-2
Р4(2) = 6 * 0,42 * 0,62 = 6 * 0,16 * 0,36 = 0,3456
k = 3 Р4(3) = С43 * р3 * (1 – р)4-3
Р4(3) = 4 * 0,43 * 0,61 = 4 * 0,064 * 0,6 = 0,1536
k = 4 Р4(4) = С44 * р4 * (1 – р)4-4
Р4(4) = 1 * 0,44 * 0,60 = 0,0256 * 1 = 0,0256
Построим ряд распределения:
Проверим условие нормировки: 0,1296 + 0,3456 + 0,3456 + 0,1536 + 0,0256 = 1.
б) Многоугольник распределения – диаграмма, которая позволяет наглядно представить закон распределения случайной величины Х:
в) Математическое ожидание дискретной случайной величины определяется по формуле:
где xi – возможные значения случайной величины Х; pi – соответствующие этим значениям вероятности. Рассчитаем математическое ожидание случайной величины Х: М(Х) = 0 * 0,1296 + 5 * 0,3456 + 10 * 0,3456 + 15 * 0,1536 + 20 * 0,0256 = 8 Вывод: среднее число очков, которое может получить стрелок, равно 8.
Дисперсию дискретной случайной величины определим по формуле:
D(X) = 02 * 0,1296 + 52 * 0,3456 + 102 * 0,3456 + 152 * 0,1536 + 202 * 0,0256 – 82 = 24 Среднее квадратичное отклонение представляет собой корень из дисперсии:
Вывод: число полученных очков может отличаться от математического ожидания (равного 8) в среднем на 4,9.
г) Определим функцию распределения случайной величины Х. Аналитическая запись функции распределения складывается из отдельных записей для каждого диапазона, на которые разбивается числовая ось возможными значениями случайной величины Х. Число диапазонов равно n+1, где n – число возможных значений случайной величины. n=5, значит, число диапазонов равно 6. Для дискретной случайной величины т.е. чтобы найти значение функции распределения для значения аргумента х, нужно сложить все вероятности, соответствующие значениям случайной величины, меньшим, чем х.
Построим график функции F(x):
д) Чтобы определить вероятность попадания значений случайной величины в заданный интервал, следует использовать формулу: P(a ≤ X < b) = F(b) − F(a), где а – нижняя граница заданного интервала; b – верхняя граница заданного интервала; F(b) − функция распределения случайной величины при Х = b; F(a) – функция распределения случайной величины при Х = a.
Определим вероятность того, что стрелок получит менее 10 очков: a = 0, b = 10 P(0 ≤ X < 10) = F(10) − F(0) Значения функции распределения при Х=10 и Х=0 определим из аналитической записи функции F(x) в п. г): значение Х=0 входит в первый интервал, значит, F(0) = 0, значение Х=10 входит в третий интервал, значит, F(10) = 0,4752. P(0 ≤ X < 10) = 0,4752 – 0 = 0,4752. Таким образом, в 47,52% случаев стрелок получит менее 10 очков.
Определим вероятность того, что стрелок получит от 5 до 15 очков. Преобразуем заданный интервал таким образом, чтобы он соответствовал формуле для определения вероятности: Р(5 ≤ Х ≤ 15) = Р(5 ≤ Х < 20) a = 5, b = 20 P(5 ≤ X < 20) = F(20) − F(5) = 0,9744 – 0,1296 = 0,8448. Таким образом, в 84,48% случаев стрелок получит от 5 до 15 очков.
Определим вероятность того, что стрелок получит более 10 очков. Преобразуем заданный интервал таким образом, чтобы он соответствовал формуле для определения вероятности: Р(10 < Х < ¥) = Р(15 ≤ Х < ¥) a = 15, b = ¥ P(15 ≤ X < ¥) = F(¥) − F(15) = 1 – 0,8208 = 0,1792. Таким образом, в 17,92% случаев стрелок получит более 10 очков.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,






 ,
,

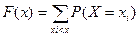 ,
,
