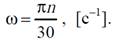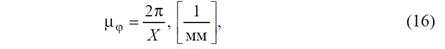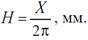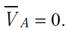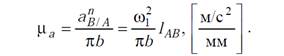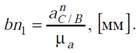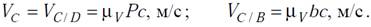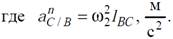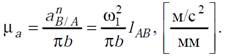КИНЕМАТИЧЕСКИЙ АНАЛИЗ РЫЧАЖНЫХ МЕХАНИЗМОВ

Методические указания к выполнению практической работы

1. ОБЩИЕ СВЕДЕНИЯ

Любой механизм предназначен для преобразования движения входных звеньев в требуемые движения выходных звеньев. Эти движения описываются посредствам кинематических характеристик, которые включают координаты точек и звеньев, их траектории, скорости и ускорения. Целью кинематического анализа является определение кинематических характеристик механизма.

Число независимых друг от друга движений, которые совершаются механизмом равно числу его степеней свободы W и числу обобщённых координат, которые приписываются входным звеньям. Например, звено 1, вращающееся вокруг неподвижной оси, т.е. образующее со стойкой 0 вращательную кинематическую пару (рис. 1, а), имеет одну степень свободы, и его положение определяется одним параметром – угловой координатой φ.

Рис. 1

Звено перемещающееся поступательно относительно стойки (рис. 1, б) также имеет одну степень свободы и его положение определяется одним параметром – координатой S.

Функцией положения механизма называется зависимость углового или линейного перемещения выходного звена от времени или обобщённой координаты механизма.

Кинематическими передаточными функциями механизма называются производные от функции положения по обобщённой координате. Первая производная называется первой передаточной функцией или аналогом скорости:

Вторая производная называется второй передаточной функцией или аналогом ускорения:

Кинематическими характеристиками механизма называются производные от функции положения по времени. Первая производная называется скоростью:

вторая производная называется – ускорением:

Связь кинематических характеристик и передаточных функций механизма определяется следующими соотношениями:

Первая передаточная функция равна отношению скоростей выходного и входного звеньев, т.е. является передаточным отношением от выходного звена к входному. Согласно уравнению (11):

где n – номер выходного звена механизма.

На практике скорость вращения входного звена нередко задаётся в виде частоты вращения n, исчисляемой количеством оборотов в минуту [об./мин.]. Связь между частотой вращения и угловой скоростью выражается зависимостью:

2. МЕТОД КИНЕМАТИЧЕСКИХ ДИАГРАММ

Наглядное представление о законе движения интересующего нас звена или точки дают кинематические диаграммы, т.е. графические изображения кинематических передаточных функций. Эти диаграммы могут быть построены методом графического дифференцирования функции положения механизма (S(φ) или ψ(φ)). При этом функция положения определяется после построения в масштабе ряда положений механизма, соответствующих одному кинематическому циклу, т.е. одному обороту ведущего звена. Планы механизма строятся в масштабе.

где l_AB– длина кривошипа, м;

АВ – длина отрезка, изображающего кривошип на плане механизма, мм.

На рисунке 2 показаны 12 планов положений кривошипно-ползунного механизма, которые соответствуют 12 (равноудалённым на угол 30°) положениям кривошипа АВ. При этом угол поворота кривошипа φ отсчитывается от его начального положения АВ_Н. Из планов механизма можно получить функцию положения S(φ) ползуна, отсчитывая координату точки С от начального положения С_Н.

Рис. 2

Для построения диаграммы S(φ) проводим оси координат S и φ (рис. 3, а). На оси φ откладываем 12 равновеликих отрезков, соответствующих положениям кривошипа. Через точки 1, 2, 3, и т. д. проводим ординаты и откладываем на них отрезки 1–1’, 2–2’, 3–3’, т. д., равные координатам точки С, отсчитываемым от крайнего левого положения С_Н. Соединяя точки 0, 1’, 2’, 3’, …, 12’ плавной кривой, получим диаграмму S(φ).

Масштаб перемещений точки С – μ_S [м/мм], равен масштабу планов механизма μ_l , если отрезки, изображающие перемещение ползуна были перенесены на диаграмму без изменения размеров. В противном случае необходимо пересчитать μ_S. Масштаб углов φ по оси абсцисс диаграммы S(φ) равен

где Х, мм – отрезок по оси φ, изображающий полный оборот кривошипа (2π).

Для построения диаграммы V_q(φ) графически продифференцируем диаграмму S(φ) по методу хорд. На участках изменения угла φ кривую S(φ) можно с достаточной степенью точности заменить рядом хорд 0–1’, 1’–2’, 2’–3’ и т.д. (рис. 3,а). Следовательно, движение с непрерывно меняющейся скоростью заменяется движением с различными, но постоянными для каждого участка скоростями. Скорость на каждом участке считается равной средней скорости истинного движения.

Координатные оси графика V_q(φ) выбираются так, чтобы ось ординат этого графика находилась на одной прямой с осью ординат графика S(φ) (рис. 3, б). Ось абсцисс графика V_q(φ) разбивается на участки, равные соответствующим участкам диаграммы S(φ). На оси абсцисс выбирается полюс P , отстоящий на полюсном расстоянии H от начала координат. Из полюса P проводятся лучи Р–1’’, Р–2’’, Р–3’’ и т.д., параллельные соответствующим хордам 0–1’, 1’–2’, 2’–3’ и т.д. Эти лучи отсекают на оси V_q отрезки пропорциональные средним скоростям на соответствующих участках. Откладывая эти отрезки в виде ординат посередине соответствующих промежутков и соединив их плавной кривой, получим график аналога скорости. Построенная таким образом диаграмма с достаточной точностью выражает закон изменения скорости исследуемой точки С.

Таким же приёмом дифференцируя график V_q(φ) строится диаграмма аналога ускорения исследуемой точки а_q(φ) (рис. 3, в).

Масштабный коэффициенты по оси ординат полученных диаграмм определяются по формулам:

При графическом дифференцировании полюсное расстояние Н рекомендуется принимать равным или кратным величине

Если указанное равенство соблюдается при построении интегральных кривых, то μ_S = μ_Vq = μ_aq.

Для проверки правильности построений диаграмм следует руководствоваться следующими закономерностями:

– точке перегиба графика перемещения должны соответствовать максимальная и минимальная ординаты графика скоростей;

– максимальной и минимальной ординатам графика перемещения должны соответствовать ординаты, равные нулю на графике скоростей;

– точка перегиба графика скоростей соответствует максимуму или минимуму графика ускорений;

– максимальной и минимальной ординатам графика скорости должны соответствовать ординаты, равные нулю на графике ускорений.

Это видно из сопоставления кинематических диаграмм (рис. 3). Указанные положения следует учитывать при графическом дифференцировании.

Рис. 3

Если выходное звено механизма совершает вращательное движение, то при кинематическом исследовании проводят построение диаграмм ψ(φ); ω_q(φ); ε_q(φ), для которых масштабы определяют по следующим зависимостям:

где ψ_max – угол размаха коромысла в радианах;

Y, мм – ордината диаграммы ψ(φ), соответствующая углу размаха ψ_max.

Используя зависимости (10 – 13) по кинематическим диаграммам можно определить скорость и ускорение исследуемой точки в любом положении механизма.

Анализ движения точек механизма методом кинематических диаграмм оправдан в случае, когда нужно быстро получить приблизительную картину изменения скоростей и ускорений, при невысоких требованиях к точности определения их величин. Для расчётов с большей точностью используют графоаналитический метод планов или аналитические методы кинематического анализа.

2. МЕТОД ПЛАНОВ СКОРОСТЕЙ И УСКОРЕНИЙ

Метод планов скоростей и ускорений даёт возможность определить линейные скорости, ускорения всех точек механизма и угловые скорости и ускорения всех звеньев механизма в данном его положении. При этом с достаточной точностью определяются не только численные значения векторов, но и их направление.

Планами скоростей и ускорений механизма называют векторные изображения этих кинематических характеристик, соответствующие заданному положению механизма.

Звенья механизма совершают сложные движения, поэтому при кинематическом анализе их кинематические характеристики исследуются одновременно в неподвижной и подвижной системах отсчёта. Движение точки звена относительно неподвижной системы отсчёта называется абсолютным. Движение точки звена относительно подвижной системы отсчёта называется относительным. Движение подвижной системы отсчёта относительно неподвижной называется переносным. Таким образом абсолютное движение точки звена можно представить, как сумму переносного и относительного движений. При этом движение характерных точек механизма рассматривается относительно точек, движение которых известно. Двигаясь последовательно от входного звена механизма к выходному, в соответствии с его структурой, можно определить кинематические характеристики всех звеньев и отдельных точек механизма.

Кинематический анализ методом планов покажем на примере простейших рычажных механизмов.

Кривошипно-ползунный механизм.

Из 12 положений механизма (рис. 2) для кинематического анализа выберем например положение 2, которое показано на рис. 4.

Исходными данными для анализа являются ω₁, l_AB, l_BC, е. Составим векторные уравнения для построения плана скоростей.

Точка А неподвижна, поэтому для неё можно записать:

Точка В вращается относительно точки А, следовательно:

где V̅ _A – вектор переносной скорости;

V̅ _B/A– вектор относительной скорости.

Модуль вектора V̅ _B/Aопределяется по формуле

V_B/A= w₁ l_AB .

Рис. 4

Вектор V̅_B/Aперпендикулярен звену АВ и направлен в сторону его вращения. Направление векторов указывается при записи векторного уравнения под соответствующим вектором.

Скорость точки С можно определить рассмотрев её движение относительно точки В и относительно точки D, расположенной на направляющей ХХ, совпадающей с точкой С. Точки В и С принадлежат одному звену и удалены друг от друга на расстояние l_BC. При движении звена 2 относительное движение этих точек будет вращательным, причём вектор относительной скорости V̅_С/Внаправлен перпендикулярно линии ВС. То есть можно записать:

Точки С и D принадлежат двум звеньям, соединённым поступательной кинематической парой, и в данный момент совпадают. Таким образом движение точки С относительно D поступательное, причём вектор относительной скорости V̅_С/Dнаправлен параллельно направляющей:

Используя векторные уравнения, построим план скоростей. Выберем точку на плоскости и обозначим её за полюс Р. В полюс будем помещать все точки, скорости которых равны нулю (точки А и D). Точки на плане скоростей будем обозначать строчными буквами. В соответствии с уравнением (19) отложим из точки Р вектор P̅b̅ перпендикулярный отрезку АВ на плане механизма и направленный в сторону вращения кривошипа. Определим масштабный коэффициент плана скоростей:

Длину отрезка Pb выбирают произвольно (обычно около 40 мм). Если отрезок Pb выбран равным отрезку АВ схемы механизма, то коэффициент μ_V называют масштабом кривошипа. Желательно, чтобы численное значение μ_V было удобным для расчётов (например 0,1; 0,01, и др.).

Определим положение точки с на плане скоростей. На основании уравнения (20) через точку b проведём линию, перпендикулярную отрезку ВС плана механизма. На основании уравнения (21) через полюс Р (в котором находится точка d) проведём линию параллельную ХХ. Так как вектора V̅_С/Ви V̅_С/Dдолжны лежать на этих линиях и приходить в одну точку с, то точка пересечения этих прямых будет являться точкой с плана скоростей. Направления векторов (стрелки) наносятся в соответствии с векторными уравнениями. Вектор P̅с̅ отображает абсолютную скорость точки С, а вектор b̅с̅ – относительную скорость V̅_С/В. Величины этих скоростей определяются по формулам:

Мгновенную угловую скорость шатуна 2 определим как

Мысленно перенесём вектор V̅_С/Вв точку С плана механизма и определим направление w₂ согласно движению точки С относительно точки В, т.е. по часовой стрелке.

Часто требуется определить кинематические характеристики какой либо точки звена (например, точка S₂ – центр масс шатуна). Для этого пользуются теоремой подобия: «Отрезки прямых линий, соединяющие точки на схеме механизма, и отрезки прямых линий, соединяющие концы векторов относительных скоростей этих точек на плане скоростей образуют подобные и сходственно расположенные фигуры». То есть, если точка S₂ делит звено ВС пополам, то она будет находиться на середине вектора b̅c̅ плана скоростей. Аналогичный подход применим и при построении плана ускорений. Соединив точку S₂ и точку Р, получим вектор абсолютной скорости точки S₂. Величина этой скорости:

Запишем векторные уравнения для построения плана ускорений.

Точка А неподвижна, поэтому для неё можно записать:

Рассматривая движение точки В относительно точки А получим:

где a̅ ⁿ_B/A и a̅ ^t_B/A– нормальная и тангенциальная составляющие ускорения вращательного движения точки В относительно А.

Вектор a̅ ⁿ_B/A направлен от точки В к центру вращения – точке А (т.е. параллельно звену АВ). Вектор a̅ ^t_B/A направлен перпендикулярно звену АВ, в сторону его углового ускорения ε₁ . Модули векторов равны:

При равномерном вращении кривошипа w₁ = const , т.е. ε₁ = 0, следовательно a̅ ^t_B/A = 0.

Для вращательного движения точки С относительно точки В можно записать:

Вектор направлен от точки С к центру вращения – точке В (т.е. параллельно звену ВС) и равен по модулю:

Вектор a̅ ^t_С/В направлен перпендикулярно звену ВС. Модуль его неизвестен, так как неизвестно угловое ускорение шатуна ε₂ .

При рассмотрении поступательного движения точки С относительно неподвижной точки D, принадлежащей направляющей ползуна, можно записать:

Для построения плана ускорений выберем точку на плоскости за полюс и обозначим её буквой π. Отложим из полюса отрезок произвольной длины (обычно около 40 мм) параллельно звену АВ в направлении от В к А, изображающий вектор a̅ ⁿ_B/A. Так как a̅ ^t_B/A = 0, то на конце этого отрезка будет находиться точка b плана ускорений. Определим масштабный коэффициент:

Если отрезок πb выбран равным отрезку АВ схемы механизма, то коэффициент μ_a называют масштабом кривошипа.

Для построения вектора a̅ ⁿ_С/Вопределим его длину:

Построим вектор b̅n̅₁ из точки b плана ускорений в направлении от точки С к точке В схемы механизма. Из конца вектора b̅n̅₁ проведём прямую, перпендикулярную ВС – направление вектора a̅ ^t_С/В .

Ускорение точки D равно нулю, поэтому точку d помещаем в полюс. Из полюса проводим прямую, параллельно ХХ. Пересечение прямых, перпендикулярной ВС и параллельной ХХ происходит в точке с плана ускорений. Соединив точку b и точку с получим вектор относительного ускорения точки С относительно точки В. Для построения точки S₂ воспользуемся теоремой подобия. Находим середину вектора b̅с̅ , обозначаем эту точку S₂ и соединяем её с точкой π. Вектор π̅S̅₂ является вектором абсолютного ускорения точки S₂.

Используя план ускорений, определяем:

Отрезок n₁c на плане ускорений соответствует вектору a̅ ^t_С/В, тогда

Для определения направления углового ускорения шатуна ε₂ , мысленно переместим вектор a̅ ^t_С/В в точку С схемы механизма. Ускорение ε₂ направлено в сторону a̅ ^t_С/В.

Плоскопараллельное движение звена механизма в каждый момент времени может быть представлено как вращение вокруг некоторой точки, которую называют мгновенным центром вращения или мгновенным центром скоростей (МЦС). Как известно из теоретической механики МЦС располагается на пересечении перпендикуляров к направлениям скоростей точек звена. Для определения МЦС шатуна 2 в его абсолютном движении, на плане механизма построим Δ BP_V2C подобный Δ bPc плана скоростей. Таким образом, если мы представим, что точка P_V2 принадлежит шатуну (рис. 4), то её скорость будет равна нулю.

Аналогично может быть найдена условная точка, принадлежащая звену, абсолютное ускорение которой в данный момент времени равно нулю. Эта точка называется мгновенным центром ускорений (МЦУ) звена. Для этого построим на плане механизма Δ BP_а2C подобный Δ bπc плана скоростей.

Шарнирный четырёхзвенник.

На рисунке 5 показан план механизма. Исходными данными для анализа являются ω₁, l_AB, l_BC, l_CD. Составим векторные уравнения для построения плана скоростей:

Скорость точки С можно определить рассмотрев её вращательное движение относительно точек В и D:

В соответствии с векторными уравнениями строим план скоростей механизма в масштабе μ_V (рис. 5). Отложим из точки Р вектор P̅b̅, перпендикулярный отрезку АВ на плане механизма и направленный в сторону вращения кривошипа. Через точку b проведём линию, перпендикулярную отрезку ВС плана механизма. Через полюс Р проведем линию, перпендикулярную отрезку СD плана механизма. Так как вектора V̅_С/Ви V̅_С/Dдолжны лежать на этих линиях и приходить в одну точку с, то точка пересечения этих прямых будет являться точкой с плана скоростей. Вектор P̅с̅ отображает абсолютную скорость точки С, а вектор b̅с̅ – относительную скорость V̅_С/В. Величины этих скоростей определяются по формулам:

Рис. 5

Определим мгновенные угловые скорости шатуна 2 и коромысла 3:

Направления w₂ и w₃ соответствуют направлениям векторов V̅_С/Bи V̅_C/D.

Соединив середину отрезка bc плана скоростей с полюсом получим вектор абсолютной скорости центра масс шатуна P̅S̅₂. Величина этой скорости:

Составим векторные уравнения для построения плана ускорений:

Для вращательного движения точки С относительно точки В можно записать:

При рассмотрении вращательного движения точки С относительно точки D, можно записать:

Для построения плана из полюса отложим отрезок πb параллельно звену АВ в направлении от В к А, изображающий вектор a̅ ⁿ_B/A. Определим масштабный коэффициент:

Для построения вектора a̅ ⁿ_С/Вопределим его длину:

Построим вектор b̅n̅₁ из точки b плана ускорений в направлении от точки С к точке В схемы механизма. Из конца вектора b̅n̅₁ проведём прямую, перпендикулярную ВС – направление вектора a̅ ^t_С/В.

Определим длину отрезка πn₂ , изображающего вектор a̅ ⁿ_С/D:

Строим вектор π̅n̅₂ в направлении от точки С к точке D схемы механизма. Из конца вектора π̅n̅₂ проведём прямую, перпендикулярную СD – направление вектора a̅^t_С/D. Пересечение прямых, соответствующих направлениям векторов a̅ ^t_С/B и a̅ ^t_С/D укажет положение точки с на плане ускорений.

Соединив точку b и точку с получим вектор относительного ускорения точки С относительно точки В. Для построения точки S₂ воспользуемся теоремой подобия. Находим середину вектора b̅с̅ , обозначаем эту точку S₂ и соединяем её с точкой π. Вектор πS₂ является вектором абсолютного ускорения точки S₂.

Используя план ускорений, определяем:

Направления ε₂ и ε₃ соответствуют направлениям векторов a̅ ^t_С/B и a̅ ^t_С/D.

Для определения положений МЦС и МЦУ шатуна 2 на плане механизма строим Δ BP_V2C ~ Δ bPc и Δ BP_а2C D ~ Δ bπc .

Не нашли, что искали? Воспользуйтесь поиском по сайту: