|
|
МЕТОД ПРОПОРЦИОНАЛЬНЫХ ВЕЛИЧИНЛекция № 2 О ЗАЗЕМЛЕНИИ ОДНОЙ ТОЧКИ СХЕМЫ
В любой электрической схеме одну любую точку схему можно заземлить, т.е. принять её потенциал равным нулю. При этом токораспределение в схеме не изменится, так как не образуется никаких новых ветвей, по которым могли бы протекать токи. Иначе будет, если заземлить две или большее число точек схемы, имеющих различные потенциалы. В этом случае образуются дополнительные ветви, сама схема становится отличной от исходной, и токораспределение в ней изменится. Возьмем для примера следующую схему: E1 = 36В; Е3 = 30В; Iк = 5А; R1 = 8 Ом; R2 = 4 Ом; R3 = 2 Ом; R4 = 2 Ом.
Рис. 1-16. Электрическая схема Заземлим любую точку схемы, например точку «а». На схеме это обозначается знаком «земля» - Расчет этой схемы методом контурных токов дал следующие значения токов в схеме: I1 = 5,6 А; I2 = 2,2 А; I3 = 7,8 А; I4 = 2,8А. ПОТЕНЦИАЛЬНАЯ ДИАГРАММА Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нём откладывают сопротивления вдоль контура, начиная с точки, потенциал которой принят за ноль, а по оси ординат – потенциалы точек. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме. Перед построением потенциальной диаграммы необходимо рассчитать потенциалы всех точек замкнутого контура, начиная с точки, потенциал которой принят за ноль. Итак, для нашей схемы имеем: φа = 0; φе = φа - I1R1 = -5,6*8 = - 44,4В; φb = φе + Е1 = -44,8 + 36 = -8,8В; φс = φb + Е3 = -8,8 + 30 = 21,2В; φd = φс - I4R4 = 21,2 – 2,8*2 = 15,6В; φа = φd – I3R3 = 15,6 – 7,8*2 = 0В. Отметим следующее правило: начиная расчет потенциалов всех точек замкнутого контура с точки, потенциал которой принят за ноль, обязательно нужно вернуться в эту точку. Это будет дополнительная проверка правильности расчёта токов. В нашем примере расчет производится для замкнутого контура aebcda. Были рассчитаны потенциалы всех точек контура, начиная с точки «а», потенциал которой был принят за ноль. Проведя расчет для всех точек контура, было доказано, что потенциал точки «а» равен нулю. На рис. 1-17 изображена потенциальная диаграмма.
Рис. 1-17. Потенциальная диаграмма
БАЛАНС МОЩНОСТЕЙ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ ПОСТОЯННОГО ТОКА При протекании токов по резисторам, в них выделяется тепло. На основании закона сохранения энергии количество тепла, выделяющееся в единицу времени в резисторах схемы, должно равняться энергии, доставляемой за то же время источниками питания. Иначе говоря, мощность источников энергии должна равняться мощности приемников электрической энергии: Ри = Рпр . Мощность источника ЭДС равна произведению ЭДС Е на ток I, протекающий через источник. Если направление ЭДС Е и тока I совпадают, то в уравнении энергетического баланса это слагаемое войдет с положительным знаком, если не совпадают – то с отрицательным знаком. Мощность источника тока равна произведению источника тока Iк на напряжение на резисторе, параллельно к которому подключен источник тока Iк. В нашем примере мощность источника тока Iк*Udc. Отметим, что напряжение Udc берётся в направлении тока от источника тока, протекающего через данный резистор. В данной схеме ток от источника тока Iк течет через резистор R4 в направлении от узла «d» к узлу «c». Поэтому использовалось направление Udc : Udc = -I4R4. (1-34) Мощность источников электрической энергии для рассматриваемой схемы равна: Pи = E1I1 + E3I3 + IkUdc = 36*5,6 + 30*7,8 + 5(-2,8*2) = 407, 6 Вт. (1-35) При подсчёте мощностей приёмников используется закон Джоуля-Ленца: Рпр = I21R1 + I22R2 + I23R3 + I24R4 = 5,62*8 + 2,22*4 + 7,82*2 + 2,82*2 = = 407,6 Вт. (1-36) Из расчетов видно, что уравнение энергетического баланса соблюдается. Если уравнение баланса соблюдается, значит токи в схеме рассчитаны верно. Это самый надежный способ проверки правильности расчёта токов в схеме. МЕТОД ПРОПОРЦИОНАЛЬНЫХ ВЕЛИЧИН В чистом виде метод применим для расчёта цепей, состоящих только из последовательных и параллельных соединений резисторов и наличии в схеме одного источника. Согласно методу пропорциональных величин, в самой удаленной от источников ЭДС ветви схемы произвольно задаёмся некоторым током, например 1А. Далее продвигаемся от конца схемы к началу и находим токи в ветвях и напряжения на различных участках схемы. В результате расчета получаем значение напряжения в начале схемы и значения токов в ветвях, если бы в самом удаленной ветви протекал ток 1А. Так как найденное значение напряжения в начале схемы в общем случае не будет равняться ЭДС источника, то следует во всех ветвях изменить токи, умножив их на коэффициент, равный отношению ЭДС источника к найденному значению напряжения в начале схемы. Рассмотрим пример (рис. 1-18):
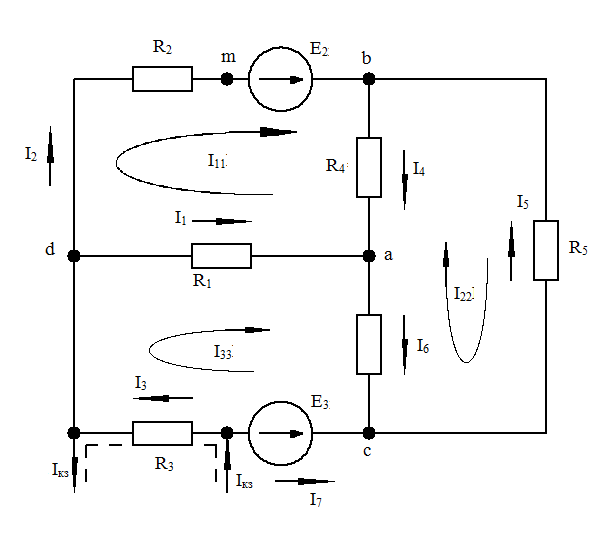
E = 100 В; R1 = 3 Ом; R2 = 13 Ом; R3 = 3 Ом; R4 = 2 Ом; R5 = 4 Ом.
Рис. 1-18. Электрическая схема
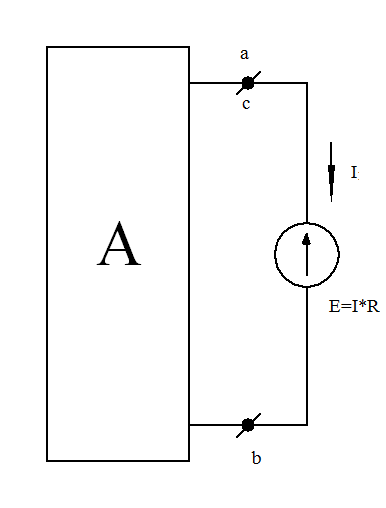
Зададимся током 1А в резисторе R5: I5 = 1А. Напряжение Ucd = R5*I5 = 1*4 = 4 В; Ток I4 = I3 = I4 + I5 = 2+1 = 3А; Напряжение Ubd = Ucd + R3I3 = 4+3*3 = 13В; Ток I2 = I1 = I2 + I3 = 1+3 = 4А. Напряжение Uad = Ubd + R1I1 = 13+4*3 = 25В. Так как ЭДС Е = 100В, то все токи надо умножить на коэффициент К: К = Таким образом, токи в исходной схеме буду равны: I1 = 16 А; I2 = 4 А; I3 = 12 А; I4 = 8 А; I5 = 4 А. ТЕОРЕМА КОМПЕНСАЦИИ В любой электрической цепи без изменения в ней токораспределения резистор может быть заменён ЭДС, численно равной падению напряжения в заменённом резисторе и направленной встречно току в этом резисторе. Для доказательства теоремы компенсации выделим из схемы одну ветвь с резистором сопротивления R, по которой течет ток I, а всю остальную часть схемы условно обозначим прямоугольником (рис. 1-19, а):
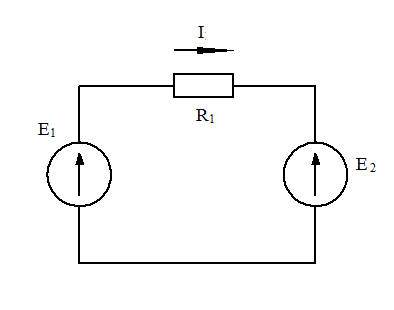
а) б) в) Рис. 1-19. К доказательству теоремы компенсации Если в выделенную ветвь включить две равных и противоположно направленных ЭДС Е, численно равных падению напряжения в сопротивлении R резистора от тока I (рис. 1-19,б) E=I*R, (1-37) то ток I в цепи от этого не изменится. Убедимся в том, что разность потенциалов между точками «а» и «с» в схеме при этом будет равна нулю. Действительно, φс = φа – IR + Е = φа – IR + IR = φа . (1-38) Но если φс = φа , то точки «а» и «с» можно объединить в одну точку или, другими словами, закоротить участок «ас» и получить схему рис.1-19 в). В ней вместо резистора сопротивлением R включена ЭДС Е. Убедимся в тождественности схем рис. 1-19, а и 1-19, в
Рис. 1-20. Тождественность схемы В схеме рис. 1-20, а ток I = Таким образом, замена сопротивления рис. 1-20,б, как это и следует из теоремы компенсации, не вызвала изменения тока в схеме. МЕТОД КОНТУРНЫХ ТОКОВ Как показал Максвелл ещё в 1873 году, число уравнений для расчёта токов и напряжений в цепи может быть уменьшено, если составлять их только по одному из законов Кирхгофа, то есть только для контуров или только для узлов. Ток в любой ветви электрической цепи всегда можно представить составленным из нескольких токов, каждый из которых замыкается по своему контуру, оставаясь вдоль него неизменным. Такие составляющие действительных токов называют контурными токами. Ток в любой ветви, принадлежащий только одному контуру, совпадает с контурным током. Ток в ветви, принадлежащей двум или нескольким контурам, равен алгебраической сумме соответствующих контурных токов. Контурные токи, проходя через узел, остаются непрерывными, следовательно, первый закон Кирхгофа выполняется автоматически. Поэтому уравнения с контурными токами составляются только по второму закону Кирхгофа. Число таких независимых уравнений равно числу независимых контуров. Рассмотрим метод контурных токов на схеме рис. 1-21.
Рис. 1-21. Схема электрической цепи В схеме рис. 1-21 число ветвей В равно семи, число узлов У равно пяти. Число уравнений, которые нужно составить по второму закону Кирхгофа К2 = В – (У – 1) = 7 – (5 – 1) = 3. Число независимых контуров Кнк в данной схеме так же равно трём: Кнк = 3. Это и будет число уравнений, которые нужно составить для расчёта токов по методу контурных токов: Кмкт = К2 = Кнк = 3. Выберем произвольно независимые контуры, например, контуры admba, acnda, abca. Так же произвольно выберем направления контурных токов, например по часовой стрелке на схеме рис. 1-21. Система контурных уравнений в наиболее общем случае, то есть когда в схеме имеются источники ЭДС и источники тока, имеет следующий вид: I11R11 + I22R12 + I33R13 + IКЗR1K = E11; I11R21 + I22R22 + I33R23 + IКЗR2K = E22; (1-40) I11R31 + I22R32 + I33R33 + IКЗR3K = E33. Здесь Rkk – суммарное сопротивление к-ого контура; R11 = R1 + R2 + R4 – суммарное сопротивление первого контура; R22 = R4 + R5 + R6 – суммарное сопротивление второго контура ; R33= R1 + R3 + R6 – суммарное сопротивление третьего контура; Rkn = Rnk - взаимное сопротивление между к-ым и n-ым контурами. Знак взаимного сопротивления берётся положительным, если контурные токи на этой ветви совпадают, и отрицательным – если не совпадают. Запишем все взаимные сопротивления: R12 = R21 = - R4; R13 = R31 = - R1; R23 = R32 = - R6. R1k, R2k, R3k – это сопротивление первого, второго или третьего контуров соответственно, по которым замыкается ток от источника тока. Перед написанием этих сопротивлений необходимо выбрать путь, по которому замыкается ток от источника тока Iкз. С целью некоторой экономии времени расчета выберем кратчайший путь через резистор R3 третьего контура. Этот путь на схеме рис. 1-21 обозначим штриховой линией. По сколько в первом и втором контурах нет резисторов, по которым замыкается ток от источника тока Iкз, то R1k = R2k = 0. И только в третьем контуре есть резистор R3, по которому замыкается ток от источника тока Iкз. Это сопротивление берётся положительным, если контурный ток и ток от источника тока на этом резисторе совпадают, и отрицательным – если не совпадает. В нашем случае: R3k = R3, (1-41) Екк – суммарная ЭДС к-ого контура. Если ЭДС совпадет с направлением контурного тока, то она берётся положительной, и если не совпадает – отрицательной: Е11 = Е2; Е22 = 0; Е33 = -Е3. (1-42) Далее нужно подставить численные значения сопротивлений резисторов, величины ЭДС и источника тока и решить системы уравнений для трёх неизвестных контуров токов I11, I22, I33. Для решения проще всего воспользоваться методом Крамера. Определим далее токи в ветвях через контурные токи. Если контурный ток совпадает с направлением тока ветви, то он берётся положительным, если не совпадает – отрицательным. I1 = I33 – I11; (1-43) I2 = I11; (1-44) I3 = I33 + Iкз; (1-45) I4 = I11 – I22; (1-46) I5 = - I22; (1-47) I6 = I33 – I22; (1-48) I7 = - I33. (1-49) Из написанных токов выбивается из общего правила только ток I3, при расчёте которого кроме контурного тока нужно учесть ещё и ток от источника тока Iкз, который в выражении тока I3 входит со знаком «плюс», если совпадает с обозначенным направлением тока I3, и со знаком «минус» - если не совпадают.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 .
.

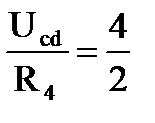 = 2А;
= 2А;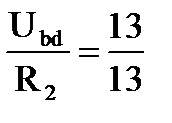 = 1А;
= 1А;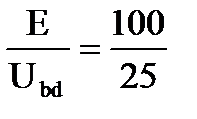 = 4.
= 4.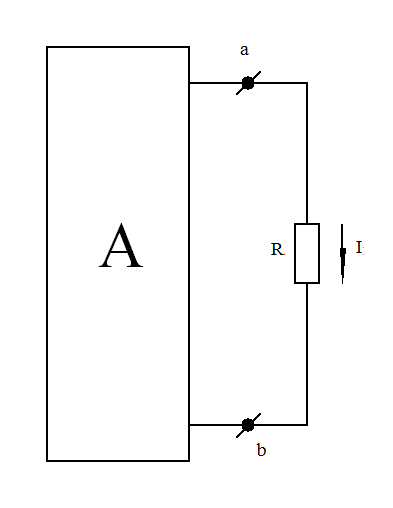


 а) б)
а) б)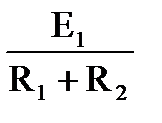 . Для схемы рис. 1-20,б ток равен I =
. Для схемы рис. 1-20,б ток равен I = 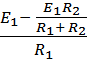 =
= 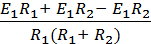 =
= 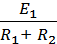 . (1-39)
. (1-39)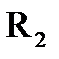 на ЭДС Е2 = IR2 в схеме
на ЭДС Е2 = IR2 в схеме