|
|
Коэффициент корреляции (параметрический).12 Основы корреляционного анализа.
Наиболее простой вид связи между переменными величинами -- это функциональная зависимость:y=f(x). Каждому значению x соответствует одно значение y. В медицине и биологии чаще встречается более сложный вид зависимости, когда каждому x соответствует множество значений y -- это корреляционная зависимость.
То есть имеем целое «облако» из точек в системе координат. Каждому значению xi соответствуем множество значений y, среднее арифметическое этих значений y̅i называется условным средним. Таким образом, среди множества точек с изменением xможно выделить точки, соответствующие условным средним y: y̅₁, y̅₂, y̅₃,….y̅n. Если соединить эти точки кривой линией, то получим линию регрессии, а соответствующая ей функция y=y̅(x) -- функция регрессии. Точно также, при изменении значений y, каждому yiсоответствует множество значений x, их средние арифметические x̅i -- условные средние, соединив их кривой , получаем вторую линию регрессии, ей соответствует функция регрессии: x=x̅(y). x̅,y̅ -- общие средние. Это средние арифметические, вычисленные по всем значениям x и y. Следовательно, в отличии от функциональной зависимости, корреляционная зависимость характеризуется двумя линиями регрессии: В настоящее время изучение различных корреляций является важным разделом многих биологических дисциплин, поэтому возникает потребность в количественном измерении корреляции. Для этого служит ряд методов, наиболее распространённым из которых является вычисление коэффициента корреляции -- это количественная характеристика связи (зависимости) между исследуемыми величинами. Дисперсия суммы случайных величин. Корреляционный момент. Xи Y-- случайные величины. (1) Z=X+Y -- их сумма. (2) M[Z]=M[X]+M[Y] Найдём D[Z]=D[X+Y] , для этого вычтем из уравнения (1) уравнение (2): (3) Z-M[Z]=X+Y-M[X]-M[Y]=(X-M[X])-(Y-M[Y]) Для сокращения записи обозначают: Z-M[Z]=ΔZ X-M[X]=ΔX Эти величины называют моментами. Y-M[Y]=ΔY Момент -- это отклонение каждого значения случайной величины от её математического ожидания. Возведём уравнение (3) в квадрат: (Z-M[Z])2=((X-M[X])+(Y-M[Y]))2 ΔZ2=(ΔX+ΔY)2 , тогда ΔZ2=ΔX2+ΔY2+2·ΔX·ΔY -- это сумма квадратов отклонений. Математическое ожидание от суммы квадратов отклонений это дисперсия: D[Z]=D[X+Y]=M[ΔZ2]=M[ΔX2]+M[ΔY2]+2·M[ΔX·ΔY]=D[X]+D[Y]+2·M[ΔX·ΔY] Принято обозначение: M[ΔX·ΔY]=K[X,Y] -- корреляционный момент. Основное свойства корреляционного момента: если величины Xи Y независимы, то их корреляционный момент K[X,Y]=0. Обратное утверждение неверно. Из последнего утверждения следует: Теорема сложения дисперсий. Если величины Xи Y независимы, то: D[X+Y]= D[X]+D[Y] Этой теоремой пользуются в теории погрешностей, при обработке результатов косвенных измерений. Так как входящие в расчётные формулы величины в большинстве случаев независимы, то подсчитывая среднюю квадратическую погрешность, суммируют квадраты всех их погрешностей.
Коэффициент корреляции (параметрический). Корреляционный момент K[X,Y] – размерная величина, то есть зависит от выбора единицы измерения. Это затрудняет сравнение корреляционных моментов различных случайных величин, поэтому удобнее использовать безразмерную величину -- коэффициент корреляции:
Но мы имеем дело с выборкой, n конечно, выборочные оценки M[X] и M[Y] -- это x̅ и y̅ -- общие средние (средние арифметические всех значений X и Y, которые мы имеем из выборки). Поэтому для вычисления коэффициента корреляции для выборки, используют формулу:
Свойства коэффициента корреляции: 1). -1≤R[X,Y]≤+1 если R[X,Y]˃0 то корреляция называется положительной, если R[X,Y]<0 то корреляция называется отрицательной. 2). если R[X,Y]≈1, зависимость между X и Y близка к линейной. 3). y=ax+b x=cx+d Так как мы имеем дело с выборочной совокупностью, то имеем не множество значений X и Y, а несколько пар выборочных значений: (xi,yi), i=1
Так как коэффициент корреляции R[X,Y] вычисляется по выборке, то есть является статистической оценкой ρ[X,Y]-- коэффициента корреляции генеральной совокупности, то R[X,Y] вычислен с ошибкой. Встаёт вопрос: достоверно ли значение выборочного коэффициента корреляции? 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
уравнение регрессии.
-- это коэффициент корреляции для генеральной совокупности.
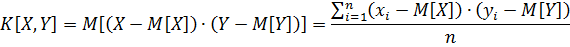
-- средние квадратические отклонения при n→∞
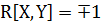, то X и Yсвязаны линейной зависимостью: