
|
|
Отделение корней способом половинного деления12 Тема 1. Численные методы алгебры Лекция 3. Численные методы решения нелинейных и трансцендентных уравнений Цель: изучить систематизированную основу теоретических знаний по численным методам решения нелинейных и трансцендентных уравнений. Учебные вопросы: 3.1. Постановка задачи. Основные определения из алгебры нелинейных и трансцендентных уравнений. 3.2. Способы отделения корней. 3.3. Методы уточнения корней. Литература к лекции 3: [1], c.50…69; [2]2, c.30…42; [3], c.42…46.
Постановка задачи. Основные определения из алгебры нелинейных и трансцендентных уравнений. Уравнение, не сводящееся к алгебраическому уравнению с помощью алгебраических преобразований, называется трансцендентным уравнением. Простейшими трансцендентными уравнениями являются показательные, логарифмические и тригонометрические уравнения. Под алгебраическими преобразованиями уравнения F=0 понимают следующие преобразования: 1) прибавление к обеим частям уравнения одного и того же алгебраического выражения; 2) умножение обеих частей уравнения на одно и то же алгебраическое выражение; 3) возведение обеих частей уравнения в рациональную степень. Алгебраическим уравнением называется уравнение вида Рn=0, где Рn – многочлен n-ой степени от одной или нескольких переменных. Трансцендентная функция– функция, не являющаяся алгебраической функцией. Трансцендентное уравнение – уравнение, содержащее неизвестное в аргументе некоторой трансцендентной функции, например: Алгебраическая функция – : 1. Функция от одного переменного 2.Функция от n переменных Рассмотрим нелинейное уравнение одной независимой переменной x, f(x)=0, x где f(x) – любая нелинейная или трансцендентная функция, например, Нахождение корней уравнения (1) производится в два этапа: 1. Отделение корней – это нахождение таких интервалов по аргументу x, внутри каждого из которых существует только один корень уравнения (1). 2. Уточнение корней заключается в применении некоторого итерационного метода, в результате которого корень уравнения (1) может быть получен с любой наперед заданной точностью ε.
Способы отделения корней На практике наиболее часто корни уравнения (1) отделяются двумя способами: 1. Графический способ. 2. Способ половинного деления.
Графический способ отделения корней
В графическом способе строится график функции f(x) (Рис.1) и приближенно определяются ее нули или корни уравнения (1) Рис. 1. Графический метод отделения корней.
В соответствии с Рис.1 рассмотрим три ситуации: 1). 2). 3).
Отделение корней способом половинного деления
В данном способе область определения функции f(x), x В данной лекции рассматриваются только однократные (простые) вещественные корни нелинейного уравнения (1). Если уравнение (1) является алгебраическим уравнением целой степени (т.е. f(x) – многочлен n-ой степени)
То при отделении корней уравнения (2) полезно использовать теоремы общей алгебры: - основная теорема алгебры; - теорема Декарта; - теорема Гюа. Содержание этих теорем заключается в следующем: 1.Основная теорема алгебры. Число корней уравнения (2) (действительных, кратных, комплексных) в точности равно n – степени уравнения (2), причем если коэффициенты a0,a1,…,an все действительные, то возможные комплексные корни попарно сопряжены. 2. Теорема Декарта. Число положительных действительных корней уравнения (2) равно числу перемен знаков последовательности коэффициентов a0,a1,…,an (не считая нулевых коэффициентов) или меньше этого числа на четное число. Следствие. Число действительных отрицательных корней уравнения (2) равно числу постоянства знаков в последовательности коэффициентов a0,a1,…,an , не считая нулевых, или меньше этого числа на четное число. 3. Теорема Гюа. Если все корни уравнения (2) действительны, то в последовательности коэффициентов a0,a1,…,an квадраты не крайних коэффициентов больше произведения соседних, т.е.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. , удовлетворяющая алгебраическому уравнению
, удовлетворяющая алгебраическому уравнению  , где F – полином от двух переменных.
, где F – полином от двух переменных.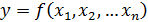 , удовлетворяющая алгебраическому уравнению
, удовлетворяющая алгебраическому уравнению  , где F – неприводимый полином от n+1 переменных.
, где F – неприводимый полином от n+1 переменных. [a,b], (1)
[a,b], (1) .
. , i=1,2,3,…
, i=1,2,3,… если
если  i =1,2, и
i =1,2, и  - знак постоянный, то на интервалах
- знак постоянный, то на интервалах  и
и  находится один корень.
находится один корень. , если
, если 
 , а
, а  , то на интервале
, то на интервале  находится двукратный корень.
находится двукратный корень. , если
, если 
 , а
, а  , то на интервале
, то на интервале  находится трехкратный корень.
находится трехкратный корень. [a,b] делят на 2,4,8,16,32,… интервала и для каждого из них анализируют знаки функции на концах интервала: если знаки противоположные, то внутри интервала находится не менее одного корня, если при этом
[a,b] делят на 2,4,8,16,32,… интервала и для каждого из них анализируют знаки функции на концах интервала: если знаки противоположные, то внутри интервала находится не менее одного корня, если при этом 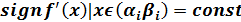 , то внутри интервала
, то внутри интервала  находится точно один корень.
находится точно один корень. , (3)
, (3) , k=1,2,…,n-1. (2а)
, k=1,2,…,n-1. (2а)