
|
|
Корректность постановки задачиИсточники и исчисление погрешностей Источники погрешностей
Существует четыре источника погрешностей в результате, полученном численным методом: 1. Математическая и физическая модель задачи. 2. Исходные данные. 3. Приближенность (погрешность) метода. 4. Округление результата. Первые два источника погрешностей приводят к так называемой неустранимой погрешности. Эта погрешность может присутствовать, даже если решение сформулированной задачи найдено точно. Погрешность метода возникает из-за того, что 1) точный оператор и исходные данные, в частности начальные и краевые условия, заменяются по определенным правилам приближенными. Так, производные заменяются их разностными аналогами, интегралы – суммами, функции – специальными многочленами; 2) при решении многих задач строятся бесконечные итерационные процессы, которые естественным образом прекращаются после конечного числа операций. Как правило,погрешность метода может быть оценена и поддается контролю. При изучении численных методов такая оценка будет сделана. Погрешность метода следует выбирать так, чтобы она была на порядок меньше неустранимой погрешности. Погрешность округления возникает в связи с тем, что вычисления производятся с конечным числом значащих цифр. Округления производятся по следующему правилу: если в старшем из отбрасываемых разрядов стоит цифра меньше 5, то содержимоесохраняемых разрядовне изменяется. В противном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа. Очевидно, что погрешность, возникающая при округлении, не превышает единицы младшего оставляемого (сохраняемого) разряда. Поскольку на современных ЭВМ число записывается, как правило, минимум с 10…12 десятичными знаками после запятой, то погрешность единичного округления
Исчисление погрешностей.
Основными количественными характеристиками погрешностей являются: 1. Абсолютная погрешность– величина
где а – точное значение некоторой величины; а* - известное приближенное значение этой же величины. 2. Относительная погрешность– величина
3. Предельной абсолютной погрешностью называется любое число
4. Предельной относительной погрешностью называется любое число
Точность- это число, характеризующее степень близости между известным приближенным значением числа а* и неизвестным точным значением аэтого же числа. Чем больше степень близости, тем выше (больше) точность. В качестве количественной оценки точности используют обратную величину от предельной погрешности, т.е. Т где Т – показатель точности;
Нормы векторов и матриц
Для исследования сходимости и точности численных итерационных методов решения задач линейной и нелинейной и нелинейной алгебры, в том числе итерационных методов решения СЛАУ и СНАУ, необходимо ввести понятие нормы векторов матриц. Нормой вектора х = В n - мерной вещественном пространстве векторов x а) б) в) Нормой матрицы Аn+n(обозначается а) б) в) г) Нормы матриц и векторов, на которые матрицы действуют должны быть согласованы. Норма матрицы А называется согласованной с нормой вектора х, на который действует матрица А; если выполняется неравенство
которое называется связью, осуществляющей согласование матрицы А с вектором х. Наиболее употребительными являются следующие нормы векторов:
Согласованными с ними с помощью связи нормами матриц будут соответственно:
Где
1.4. Основная и дополнительная литература по дисциплине. Основная: 1. Формалев В.Ф., Ревизников Д.Л. Численные методы.-М.: Физматлит 2004-400с. 2. Пирумов У.Г. (редактор). Численные методы. Учебник и практикум. Бакалавр. Академический курс.-М.: Юрайт, 2014-422с. 3. Численные методы. Сборник задач. Под редакцией У.Г.Пирумова.-М.: Дрофа, 2007-144с. Дополнительная: 4. Вержбицкий В.М. Численные методы. Три книги: 1) Линейная алгебра и нелинейные уравнения. 2) Математический анализ и ЛДУ. 3) Дифференциальные уравнения в частных производных. 5. Демидович Б.П., Марон И.А. Основы вычислительной математики.-М.: наука, 1966, - 664с.
Учебная литература к лекции 1:
Приложение к лекции 1 Корректность постановки задачи
При численном решении основных задач необходимо знать какие-либо входные (исходные) данные – начальные , краевые, (граничные) значения искомой функции, коэффициенты и правые части уравнений и т.д. Очевидно, что кроме этого для исследователя важно знать, существует ли решение поставленной задачи, единственно ли оно и как оно зависит от входных данных. Численная задача поставлена корректно, если при заданных исходных данных единственное решение, которое неправильно зависит отисходных данных, т.е. малому их изменению соответствует малоеизменение решения. В этом случае говорят, что задача устойчива. Задача поставлена некорректно,если ее решениенеустойчиво,относительно исходных данных, т.е. их малому изменениюмогут соответствовать большие изменения решения. Известно, что корректнойзадачей являетсязадачачисленного интегрирования, а некорректной задача численного дифференцирования. Классическим примером некорректной задачи является задача Коши для уравнения Лапласа. Эта некорректность исходной задачи проявляется при ее численном решении.
Актуальность дисциплины «Численные методы» В настоящее время появилась значительное число различных погрешностей программных продуктов (Math Cad, Math lab и дрю), с помощью которых, задавая только входные данные и не вникая в сущность алгоритмов, можно решить значительное число задач, на обучение решению которых и направлена дисциплина «Численные методы». Безусловно, умение пользоваться этими программными продуктами существенно сокращает время и ресурсы по решению важных задач. Вместе с этим бездумное использование упомянутых выше программ без тщательного анализа метода, с помощью которого решается задача, таит в себе следующие опасности. 1. Все методы имеют ограничения по входным параметрам (например, размер матриц при решении СЛАУ), и попытка решить задачу с входными параметрами за пределами этих ограничений приводит к неудаче. 2. Сами численные методы имеют существенные ограничения по применению. 3. Незнание метода, с помощью которого решалась конкретная задача в программном продукте, приводит к ситуации, когда трудно проанализировать качество решения (точность, сходимость, устойчивость и др. характеристики численных методов). Стандартные программные продукты значительно ограничены количеством решаемых задач, среди которых в основном линейные задачи. Вне сферы их применения остается большинство задач, связанных с уравнениями математической физики и др. Поэтому при численном решении задач вычислитель должен четко представлять каждый из следующих этапов: 1) построение адекватной математической модели, 2) выбор метода численного решения, 3) разработку алгоритма решения задачи, 4) составление программы вычислений, 5) отладка программы, 6) корректировку и исправление всех этапов, начиная с математической модели, на основе анализа тестовых результатов. Таким образом, путь от постановки задачи до получения результатов решения не краток. В связи с этим важно отметить следующее. Если неопытный вычислитель после реализации первых 4-х этапов считает, что задача решена, то опытный вычислитель знает, что неопытный вычислитель находится лишь в начале сложного пути с неожиданными результатами.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 = 10-10… 10-12 обычно пренебрежима мала по сравнению с неустранимой погрешностью и погрешностью метода. При решении больших задач производятся миллиарды операций и можно предположить, что ошибки могут заметно накапливаться, однако, поскольку они носят случайный характер, может происходить их взаимная компенсация. Зачастую строятся специальные алгоритмы, в частности итерационные, которые малочувствительны к ошибкам округления.
= 10-10… 10-12 обычно пренебрежима мала по сравнению с неустранимой погрешностью и погрешностью метода. При решении больших задач производятся миллиарды операций и можно предположить, что ошибки могут заметно накапливаться, однако, поскольку они носят случайный характер, может происходить их взаимная компенсация. Зачастую строятся специальные алгоритмы, в частности итерационные, которые малочувствительны к ошибкам округления. (а*)
(а*) (а*), удовлетворяющее условию
(а*), удовлетворяющее условию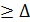 (а*).
(а*). (а*), удовлетворяющее условию
(а*), удовлетворяющее условию (а*)
(а*)  (а*).
(а*). (а*)–предельная относительная погрешность.
(а*)–предельная относительная погрешность. (обозначают
(обозначают  )
) Rn называют неотрицательное число, вычисляемое с помощью компонент вектора и обладающее следующими свойствами
Rn называют неотрицательное число, вычисляемое с помощью компонент вектора и обладающее следующими свойствами 0 (
0 (  );
); =
= 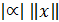 для любых чисел
для любых чисел  (действительных или комплексных);
(действительных или комплексных);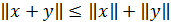 .
.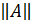 c вещественными элементами в n-мерном пространстве матриц А
c вещественными элементами в n-мерном пространстве матриц А  0 (
0 (  0 тогда и только тогда, когда А – нулевая матрица, т.е. А=
0 тогда и только тогда, когда А – нулевая матрица, т.е. А=  );
); для любых действительных и комплексных чисел
для любых действительных и комплексных чисел  +
+  ;
; для всех
для всех  матриц А и
матриц А и  рассматриваемого пространства.
рассматриваемого пространства. ∙
∙  , I =
, I =  , …
, …




 - модули собственных чисел симметрической вещественной матрицы
- модули собственных чисел симметрической вещественной матрицы  для которой все
для которой все  являются действительными числами;
являются действительными числами; - максимальное по модулю собственное значение матрицы
- максимальное по модулю собственное значение матрицы  , с.3…15;
, с.3…15;  ,с.3…6.
,с.3…6.