
|
|
Ускорение жидкой частицы.Запишем выражение для проекции ускорения жидкой частицы на какую-либо координатную ось, например, x. Имеем
Для нахождения этой величины следует учесть, что проекция скорости
Разделим обе части на dt. Имея в виду, что
Аналогичные соотношения можно записать и для двух других компонент. Выражение (4.12) носит название полной либо субстанциональной производной. Установим смысл величин, входящих в нее. Производная Анализ движения жидкой частицы. Движение жидкой частицы является более сложным, чем движение твердого тела, которое, как известно из механики, может быть поступательным и вращательным. Особенностью жидкости и ее частиц, как уже неоднократно отмечалось, является легкая деформируемость. Поэтому помимо поступательного и вращательного, жидкая частица может участвовать и в деформационном движении. Это положение и составляет суть так называемой первой теоремы Гельмгольца, к рассмотрению которой мы и приступаем. Оценивая значение работы Г.Гельмгольца, основоположник отечественной аэродинамики Н.Е.Жуковский писал, что «современная гидродинамика своим развитием обязана главным образом Гельмгольцу». Важнейшим достоинством приводимых ниже выкладок и рассуждений является то, что они раскрывают физический смысл и вносят ясность в ряд казалось бы совершенно абстрактных понятий. Выкладки эти достаточно просты, но требуют внимания. Поэтому нужно запастись определенной долей терпения и помнить, что достигаемое понимание сути явлений безусловно оправдает эти затраты труда.
Рассмотрим жидкую частицу в форме прямоугольного параллелепипеда (рис. 4.5). Длина его ребер dx, dy, dz. Деформация такой жидкой частицы может быть как линейной (ребра удлиняются и укорачиваются), так и угловой (грани скашиваются). Удобней рассмотреть каждый из этих видов раздельно. Начнем с угловых деформаций. Угловые деформации. Из рис. 4.5 следует, что угловая деформация (скашивание) может возникнуть из-за разности скоростей, перпендикулярных ребрам (частично этот вопрос уже обсуждался в разделе 2.2). Для упрощения целесообразно ограничиться лишь одной гранью, показанной на рис. 4.6. Пусть компоненты скорости в точке A равны
Аналогичные выражения можно записать и для других проекций. Рассмотрим приращение
Предположим, что за время dt за счет разности скоростей в точках A и B ребро займет положение AB'. Аналогично рассуждая относительно скорости Точка A: Точка D: За счет разности этих скоростей точка D займет позицию D'. Таким образом
Путь, проходимый точкой B за время dt в положение B', определяет величину скашивания, которую можно найти как
Угловая деформация характеризуется тангенсом угла
(имея в виду, что Вследствие малости угла Аналогично,
Полное скашивание первоначально прямого угла A определяется как сумма
Здесь следует обратить внимание на одно весьма существенное обстоятельство: рассматриваемое перемещение ребер вызвано не только деформацией, но и вращением частицы. Действительно, если бы грань только деформировалась без вращения, то ребра повернулись бы на одинаковый угол навстречу друг другу. Наоборот, если бы происходило только вращение, то ребра поворачивались бы на одинаковый угол в направлении вращения. Следовательно, в общем случае движение элемента можно рассматривать как сумму деформационного и вращательного движений, и таким образом определить Из рис. 4.7 следует, что
либо откуда
Вычитая, получим
Таким образом, деформация характеризуется полусуммой углов, а вращение - полуразностью. Имея в виду (4.14), можем записать:
Скорость угловой деформации, происходящей вокруг оси z
И по аналогии
Выражение
Соотношения (4.214.23) играют исключительно важную роль в механике жидкости. Они устанавливают связь между угловой и поступательной скоростями жидкой частицы. Вопрос о знаках чисто условный. В гидромеханике поворот против часовой стрелки считается положительным, по часовой - отрицательным. В векторной форме выражение для угловой скорости может быть записано как
Заменяя
Сопоставляя выражение в квадратных скобках с формулой (1.8) видим их полную идентичность, поэтому можем записать:
либо
Формула (4.27) раскрывает гидромеханический смысл вихря (ротора) векторного поля. Если Линейные деформации.
Очевидно, что линейные деформации частицы (рис. 4.8) могут возникнуть в результате различия в скоростях, совпадающих с направлением ребер. Как и ранее, компоненты скорости в точке A - Вдоль оси x: Точка A:
Точка D: Разность скоростей, вызывающая удлинение ребра AD:
Относительное удлинение
Скорость относительного удлинения
Аналогично для других осей
Если процесс происходит одновременно вдоль всех осей, то это приводит к объемному расширению либо сжатию частицы. Таким образом, объемная деформация сводится к изменению первоначального объема параллелепипеда
Скоростью относительной объемной деформации назовем отношение изменения объема к его первоначальному объему и скорости деформации, т.е.
Если Полученную выше связь между поступательной и вращательной скоростями жидкой частицы можно получить и более коротким путем, представляющим определенный интерес. Разные подходы к одному и тому же вопросу способствуют углубленному пониманию. Поэтому рассмотрим этот путь.
Пусть жидкая частица вращается вокруг оси z с угловой скоростью
Рассмотрим точку M на жидкой частице (рис. 4.10). Линейная скорость этой частицы
Откуда находим
Таким образом
Аналогично для двух других компонент
Либо в векторной форме
что полностью совпадает с (4.26). Движение, при котором 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
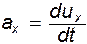
 (как и две другие проекции) является функцией координат x, y, z, которые, в свою очередь, в общем случае зависят от времени t. Представим величину
(как и две другие проекции) является функцией координат x, y, z, которые, в свою очередь, в общем случае зависят от времени t. Представим величину  в виде полного дифференциала
в виде полного дифференциала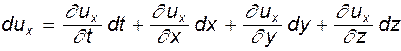
 ,
, 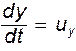 и
и  , получим
, получим (4.12)
(4.12)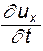 - проекция локального ускорения, которое характеризует изменение скорости во времени в данной точке пространства. Локальное ускорение обусловлено нестационарностью процесса. Из чего следует, что если движение стационарное (установившееся), то локальное ускорение отсутствует, т.е.
- проекция локального ускорения, которое характеризует изменение скорости во времени в данной точке пространства. Локальное ускорение обусловлено нестационарностью процесса. Из чего следует, что если движение стационарное (установившееся), то локальное ускорение отсутствует, т.е.  . Три остальных члена (4.12) - проекции конвективного ускорения, которое возникает при переходе частицы от одной точки пространства к другой, оно обусловлено неравномерностью скоростного поля, т.е. неравномерным распределением скоростей.
. Три остальных члена (4.12) - проекции конвективного ускорения, которое возникает при переходе частицы от одной точки пространства к другой, оно обусловлено неравномерностью скоростного поля, т.е. неравномерным распределением скоростей.
 ,
, 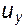 ,
,  . Найдем скорости в точке B, считая, что движение установившееся и, следовательно, все производные по t равны нулю. Приращение компоненты скорости при переходе из одной точки пространства в другую можно представить как u+du. Так для проекции
. Найдем скорости в точке B, считая, что движение установившееся и, следовательно, все производные по t равны нулю. Приращение компоненты скорости при переходе из одной точки пространства в другую можно представить как u+du. Так для проекции  , где
, где
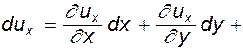
 (4.13)
(4.13) , т.е.
, т.е.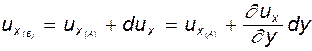

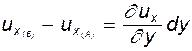
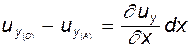
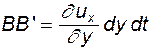
 . При этом
. При этом
 ).
). .
.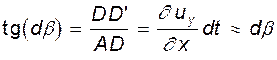
 (4.14)
(4.14)
 . Рассмотрим деформацию прямого угла A, считая, что вращение происходит против часовой стрелки. Чисто деформационное движение будем характеризовать углами
. Рассмотрим деформацию прямого угла A, считая, что вращение происходит против часовой стрелки. Чисто деформационное движение будем характеризовать углами  , а чисто вращательное -
, а чисто вращательное -  .
.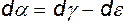
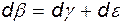
 ,
, (4.15)
(4.15) (4.16)
(4.16) (4.17)
(4.17) (4.18)
(4.18)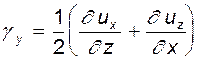 (4.19)
(4.19) (4.20)
(4.20) есть угловая скорость вращения жидкой частицы. Проекции угловых скоростей
есть угловая скорость вращения жидкой частицы. Проекции угловых скоростей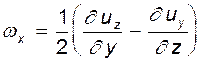 (4.21)
(4.21) (4.22)
(4.22)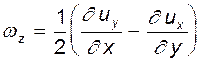 (4.23)
(4.23)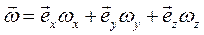 (4.24)
(4.24) ,
, 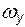 и
и  их выражениями по (4.21-4.23) получаем:
их выражениями по (4.21-4.23) получаем: (4.25)
(4.25) (4.26)
(4.26) (4.27)
(4.27)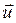 характеризует поле мгновенных скоростей, то векторное поле
характеризует поле мгновенных скоростей, то векторное поле  представляет собой поле удвоенных угловых скоростей частиц жидкости этого поля.
представляет собой поле удвоенных угловых скоростей частиц жидкости этого поля.
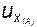
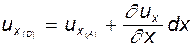
 . Удлинение частицы
. Удлинение частицы  за время dt
за время dt (4.28)
(4.28) (4.29)
(4.29) (4.30)
(4.30) ;
; 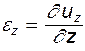
 на величину
на величину  за счет растяжения либо сжатия ребер. При этом
за счет растяжения либо сжатия ребер. При этом  , и с учетом (4.28)
, и с учетом (4.28)  . Аналогично
. Аналогично  и
и  . Таким образом
. Таким образом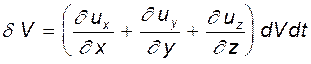
 .
. , то это означает, что
, то это означает, что  , т.е. деформация жидкой частицы происходит без изменения ее объема. В этом и заключается гидромеханический смысл равенства нулю дивергенции.
, т.е. деформация жидкой частицы происходит без изменения ее объема. В этом и заключается гидромеханический смысл равенства нулю дивергенции.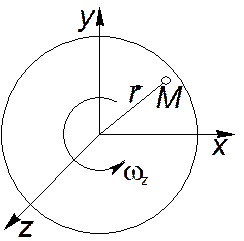
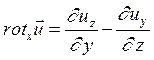
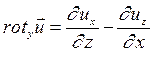


 . Запишем выражения для проекций скоростей на оси координат:
. Запишем выражения для проекций скоростей на оси координат: ;
; ;
;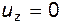
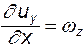 ;
;  .
.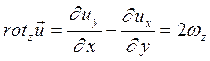
 ;
; 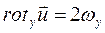
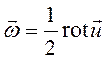
 называют вихревым, при
называют вихревым, при  - безвихревым либо потенциальным. Из чего следует, что если течение вихревое, то движение жидких частиц происходит с вращением.
- безвихревым либо потенциальным. Из чего следует, что если течение вихревое, то движение жидких частиц происходит с вращением.