
|
|
Метод Ньютона, его реализации и модификацииЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДИЧЕСКИЕ УКАЗАНИЯ К лабороторной работе ПО ДИСЦИПЛИНЕ «Численные методы»
Составитель И.А.Селиванова, ст.преподаватель. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ:Методические указания к лабораторной работе по дисциплине «Численные методы» Указания предназначены для студентов всех форм обучения направления 230100 – «Информатика и вычислительная техника».
У ФГАОУ ВПО «УрФУ имени первого СОДЕРЖАНИЕ 1. Постановка задачи.. 4 2. Метод Ньютона, его реализации и модификации.. 4 2.1.Метод Ньютона. 4 2.2.Модифицированный метод Ньютона. 8 2.3.Рекурсивный метод Ньютона. 9 3. Метод простых итераций.. 10 4. ЗАДАНИЕ НА ЛАБОРАТОРНУЮ РАБОТУ.. 12 5. Варианты заданий. 13 Список литературы.. 14
Постановка задачи Дана система
где
где Требуется найти такой вектор Для всех рассматриваемых далее методов требуется находить начальное приближение Метод Ньютона, его реализации и модификации
2.1.Метод Ньютона
Для решения системы (1.1) воспользуемся методом последовательных приближений. Предположим, что найдено
где Подставив выражение (2.1.1) в (1.2), получим:
Предположим, что функция
Под производной
Формула (2.1.3) может быть записана в следующем виде:
Отсюда, предполагая, что матрица
Теперь, подставив выражение (2.1.6) в формулу (2.1.1), окончательно получим:
Таким образом, получили вычислительную формулу (метод Ньютона), где в качестве нулевого приближения Для останова процесса вычислений в быстросходящихся методах таких, как метод Ньютона, методы секущих и т.п., часто вполне успешно применяют простой критерий:
Это можно объяснить двумя причинами. Во-первых, оценки погрешности здесь довольно «дороги». Имеется в виду как их получение (особенно для различных модификаций базовых методов), так и их реальное применение. Во-вторых, в силу своей быстрой сходимости, к моменту достижения требуемой малости нормы поправки эти методы набирают такую скорость, что зачастую «проскакивают» установленный порог точности. Т.е. выход по критерию (2.1.8) дает значение
Методика решения задачи
1. Задать начальное приближение 2. Найти значение выражения 3. Вычислить следующее приближение: 4. Если
Пример 1. Решить систему 1. Для выбора начального приближения найдем координаты точек пересечения кривых, соответствующих первому и второму уравнениям (рис. 1).
Рис. 1 Выбор начального приближения Выберем начальное приближение 20. Так как
то
30. Вычислим
40. Так как 21. Так как
31. Вычислим
41. Так как Таблица 1
Точность К недостаткам метода Ньютона следует отнести: · необходимость задавать достаточно хорошее начальное приближение; · отсутствие глобальной сходимости для многих задач; · необходимость вычисления матрицы Якоби на каждой итерации;
Достоинством метода является квадратичная сходимость из хорошего начального приближения при условии невырожденности матрицы Якоби [1].
2.2.Модифицированный метод Ньютона Если матрицу Якоби
· К преимуществам этого метода можно отнести то, что он требует значительно меньших вычислительных затрат на один итерационный шаг, т.к. матрица Якоби вычисляется только один раз. · Однако недостатком является то, что итераций при этом может потребоваться значительно больше для достижения заданной точности по сравнению с основным методом Ньютона. Критерий остановки: Методика решения задачи 1. Задать начальное приближение 2. Найти значение выражения 3. Вычислить следующее приближение: 4. Если
2.3.Рекурсивный метод Ньютона.
Компромиссный вариант – это вычисление и обращение матриц Якоби не на каждом итерационном шаге, а через несколько шагов (такие методы называют рекурсивными). Например, простое чередование основного (2.1.7) и модифицированного методов Ньютона (2.2.1) приводит к итерационной формуле:
За
Доказано, что такой процесс при определенных условиях порождает кубически сходящуюся последовательность Критерий остановки:
Методика решения задачи
1. Задать начальное приближение 2. Найти значение выражения 3. Найти значение выражения 4. Если Метод простых итераций Пусть система (1.1) имеет вид (или преобразована к виду):
или иначе, в компактной записи,
где:
Для этой задачи о неподвижной точке нелинейного отображения
которое определяет метод простых итераций (МПИ) (или метод последовательных приближений) для задачи (3.1). Если начать процесс построения последовательности Теорема 2. Пусть функция 1. 2. Тогда Однако практическая ценность такой теоремы не так велика из-за неконструктивности ее условий. В случаях, когда имеется хорошее начальное приближение Теорема 3. (о достаточном условии сходимости метода простых итераций) Пусть функции
где Если последовательные приближения Замечание Условие (3.5) выполняются, если для любого
Критерий остановки: Итерационный процесс, реализуемый согласно (3.4) соответствует параллельному итерированию, т.к. для вычисления Система (1.1) может быть преобразована к виду (3.1) различными способами, например, это можно сделать, умножив (1.1) на некоторую неособенную
Методика решения задачи 1. Задать начальное приближение 2. Вычислить
3. Если
ЗАДАНИЕ НА ЛАБОРАТОРНУЮ РАБОТУ
1. Составить и отладить программы вычисления решения системы уравнений своего варианта методами Ньютона и методом простой итерации. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 нелинейных уравнений с
нелинейных уравнений с 
 , - нелинейные функции, определенные и непрерывные в некоторой области
, - нелинейные функции, определенные и непрерывные в некоторой области  . Систему (1.1) можно представить в векторном виде:
. Систему (1.1) можно представить в векторном виде:
 ,
,  .
. , который при подстановке в систему (1.1) превращает каждое уравнение в верное числовое равенство.
, который при подстановке в систему (1.1) превращает каждое уравнение в верное числовое равенство. . В случае
. В случае  это можно сделать графически, определив координаты точки пересечения кривых, описываемых уравнениями
это можно сделать графически, определив координаты точки пересечения кривых, описываемых уравнениями  или
или 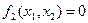 .
.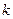 -ое приближение
-ое приближение  одного из изолированных корней
одного из изолированных корней 
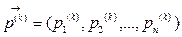 - поправка (погрешность) корня на
- поправка (погрешность) корня на 
 - непрерывно дифференцируема в некоторой выпуклой области, содержащей
- непрерывно дифференцируема в некоторой выпуклой области, содержащей  и
и 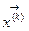 . Тогда левую часть уравнения (2.1.2) разложим в ряд Тейлора по степеням малого вектора
. Тогда левую часть уравнения (2.1.2) разложим в ряд Тейлора по степеням малого вектора 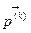 , ограничиваясь линейными членами:
, ограничиваясь линейными членами:
 следует понимать матрицу Якоби системы функций
следует понимать матрицу Якоби системы функций  , относительно переменных
, относительно переменных 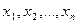 , то есть:
, то есть:

 - неособенная, получим:
- неособенная, получим:

 ,
, 
 значительно (иногда на несколько порядков) меньшее, чем
значительно (иногда на несколько порядков) меньшее, чем  . Отслеживать факт сходимости в процессе итерации для того, чтобы реагировать на возможную расходимость в случаях, когда заранее не обеспечены условия сходимости применяемого метода, можно с помощью текущих проверок на уменьшение от шага к шагу поправок и невязок, т.е. выполнение неравенств:
. Отслеживать факт сходимости в процессе итерации для того, чтобы реагировать на возможную расходимость в случаях, когда заранее не обеспечены условия сходимости применяемого метода, можно с помощью текущих проверок на уменьшение от шага к шагу поправок и невязок, т.е. выполнение неравенств: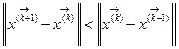 и
и 
 .
. .
. .
. и
и  , процесс закончить и положить
, процесс закончить и положить  . Иначе, положить
. Иначе, положить  и перейти к п.2.
и перейти к п.2. методом Ньютона с точностью
методом Ньютона с точностью  .
.
 . В поставленной задаче
. В поставленной задаче 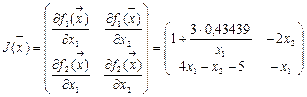
 ,
,
 ,
,
 .
.

 , то положим
, то положим  и перейдем к п.2.
и перейдем к п.2.

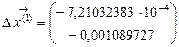

 , то положим
, то положим  и остановим вычисления. Результаты расчетов приведены в табл. 1.
и остановим вычисления. Результаты расчетов приведены в табл. 1.

 вычислить и обратить лишь один раз в методе Ньютона, то придем к модифицированному методу Ньютона
вычислить и обратить лишь один раз в методе Ньютона, то придем к модифицированному методу Ньютона
 ,
,  .
. ,
, 

 .
. .
. .
.


 запишем формально рекуррентное равенство
запишем формально рекуррентное равенство ,
, 
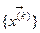 с некоторого вектора
с некоторого вектора  и продолжить по формуле (3.4), то при определенных условиях эта последовательность со скоростью геометрической прогрессии будет приближаться к вектору
и продолжить по формуле (3.4), то при определенных условиях эта последовательность со скоростью геометрической прогрессии будет приближаться к вектору  . А именно, справедлива следующая теорема.
. А именно, справедлива следующая теорема. таковы, что:
таковы, что:
 .
. сходится к
сходится к 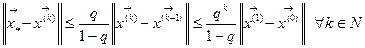 .
. и
и  ,
,  , непрерывны в области
, непрерывны в области  , причем выполнено неравенство:
, причем выполнено неравенство:
 -некоторая постоянная.
-некоторая постоянная. не выходят из области
не выходят из области  и вектор
и вектор  является в области
является в области  справедливы неравенства
справедливы неравенства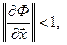
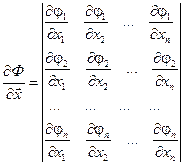
 -го приближения всех неизвестных учитываются вычисленные ранее их
-го приближения всех неизвестных учитываются вычисленные ранее их  матрицу
матрицу  и прибавив к обеим частям уравнения
и прибавив к обеим частям уравнения  вектор неизвестных
вектор неизвестных  . Полученная система
. Полученная система  эквивалентна данной, и имеет вид задачи о неподвижной точке. Проблема теперь состоит лишь в подборе матричного параметра A такого, при котором вектор-функция
эквивалентна данной, и имеет вид задачи о неподвижной точке. Проблема теперь состоит лишь в подборе матричного параметра A такого, при котором вектор-функция  обладала бы нужными свойствами.
обладала бы нужными свойствами. по формуле
по формуле 