|
|
Пример выполнения расчетно-графической работы № 212 Работа представляет собой статический расчет пространственной стержневой конструкции, опирающейся на монолитный фундамент с помощью сферических шарниров. Определяются усилия во всех стержнях конструкции методом вырезания узлов. Кроме того, выясняется общее силовое воздействие на фундамент со стороны стержневой конструкции путем приведения системы сил к заданному центру О на верхней поверхности фундамента.
Расчетная схема узла А
Уравнения равновесия 3.Σ Z = - R1 - R3 sin β = 0. При значениях функций sin α=0,6;cos α = 0,8; sin β = 0,447; cos β = 0,895 из уравнений найдем R2 = - 0,6 кН, R3 = - 0,894 кН, R1 = 0,4 кН.
Расчетная схема узла В
Уравнения равновесия 4. Σ X = R2 - R4 sin δ - R6 cos γ sin α = 0; 5.Σ Y = - R6 cos γ cos α = 0; 6.Σ Z = - F2 - R5 - R4 cos δ - R6 sin γ = 0. Значения функций sin γ = 0,37 ; cos γ = 0,93 ; sin δ= 0,6; cos δ = 0,8. Результаты решения уравнений R6 = 0, R4 = 1,0 кН, R5 = - 2,8 кН
Расчетная схема узла С
Уравнения равновесия 7. Σ X = F3 + R9 cos φ = 0, 8. Σ Y = R7 cos β - R3 cos β = 0,
Рассмотрим систему сил, действующих на фундамент со стороны стержней. При этом следует реакции растянутых стержней направлять «от узла», расположенного на фундаменте, а сжатых стержней «к узлу».
Приведем эту систему сил к заданному центру О на поверхности фундамента.Проекции главного вектора V на оси координат
Vx = Σ X = R9 cos φ + R4 sin δ = 3,6 кН; Vy = Σ Y = - R7 cos β = - 0,8 кН; Vz = Σ Z = R1 + R4 cos δ – R5 + R7 sin β + R8 – R9 sin φ = - 2,0 кН Величина главного вектора V = Проекции главного момента Mo Mox = Σ Mx = R1 0,5 b + R4 cos δ 0,5 b – R5 0,5 b + R7 sin β 0,5 b – R8 0,5 b + Moy = Σ My = R1 0,5 a+ R4 cos δ 0,5 + R7 sin β 0,5 a + R8 0,5 a + R9 sin φ 0,5 a + R5 0,5 a =11,4 кНм Moz = Σ Mz = - R4 sin δ 0,5 b + R7 cos β 0,5 a + R9 cos φ 0,5 b = 6,0 кНм Величина главного момента Mo =
Для проверки выполненных расчетов найдем проекции главного вектора и главного момента для системы заданных сил F1 , ,F2 и F3 Vx = Σ X = 3,6 кН; Vy = Σ Y = = - 0,8 кН; Vz = Σ Z = - 2,0 кН Mox = Σ Mx = F1 cos α 2h – F2 0,5b = - 0,8 кНм Moy = Σ My = F3 h + F1 sin α 2h + F2 0,5 a = 11,4 кНм Moz = Σ Mz = F3 0,5b = 3,0 x 2,0 = 6,0 кНм Результаты совпадают, следовательно, расчеты выполнены правильно. Определим, к какому простейшему виду приводится система сил. Так как V ≠ 0 и Mo ≠ 0, то система сил приводится либо к равнодействующей, либо к «динаме» - силовому винту. Найдем скалярное произведение главного момента и главного вектора Mo V cos (Mo^V) = Mx Vx + My Vy + Mz Vz Главный момент и главный вектор не перпендикулярны друг другу, следовательно система сил приводится к динаме. Моментом динамы MD называется проекция главного момента на линию действия главного вектора, поэтому MD можно найти по формуле MD = (Mox Vx + Moy Vy + Moz Vz) / V = -24 / 4,2 = -5,72 кНм Знак минус означает, что вектор MD направлен противоположно вектору V . Расположение центральной оси системы определим, исходя из того, что векторы MD и V расположены на этой оси и их одноименные проекции пропорциональны, т.е. [Mx – (y Vz – z Vy)] / Vx = [My – (z Vx – x Vz)] / Vy = = [Mz – (x Vy – y Vx)] / Vz = MD / V , где x, y и z - координаты точек, расположенных на центральной оси. Для определения координат x1 и y1 точки 1 пересечения центральной оси с плоскостью хОу выберем следующие два равенства [Mx – (y1 Vz – z1 Vy)] / Vx = MD / V, [My – (z1 Vx – x1 Vz )] / Vy = MD / V , где положим z1 = 0. { - 0,8 – [ y1 ( - 2,0 ) – z1 ( - 0,8 ) ] } / 3,6 = ( - 5,72) / 4,2 ; y1 = - 2,05 м { 11,4 – [ z1 3,6 – x1 ( - 2,0 ) ] } / ( - 0,8 ) = ( - 5,72) / 4,2 ; x1 = 5,15 м Аналогично определим координаты z2 и x2 точки 2 пересечения центральной оси с плоскостью xOz при y2 = 0 [Mx – (y2 Vz – z2 Vy)] / Vx = MD / V, [Mz – (x2 Vy – y2 Vx)] / Vy = MD / V , { - 0,8 – [ y2 ( - 2,0 ) – z2 ( - 0,8 ) ] } / 3,6 = ( - 5,72) / 4,2 ; z2 = 5,12 м { 6,0 – [ x2 ( - 0,8 ) – y2 3,6 ) ] } / ( - 2,0 ) = ( - 5,72) / 4,2 ; x2 = - 4,1 м Координаты z3 и y3 точки 3 пересечения центральной оси с плоскостью zОу ( x3 = 0) [My – (z3 Vx – x3 Vz)] / Vy = MD / V , [Mz – (x3 Vy – y3 Vx)] / Vy = MD / V { 11,4 – [ z3 3,6 – x3 ( - 2,0 ) ] } / ( - 0,8 ) = ( - 5,72) / 4,2 ; z3 = 2,86 м { 6,0 – [ x3 ( - 0,8 ) – y3 3,6 ) ] } / ( - 2,0 ) = ( - 5,72) / 4,2 ; y3 = - 0,91 м
Рекомендуемая литература
1. Яблонский А. А. Курс теоретической механики / А. А. Яблонский, В. М. Никифоров. – М.: Высшая школа, 2010. 2. Тарг С. М. Краткий курс теоретической механики / С. М. Тарг. – М.: Физматгиз, 2006. 3. Бутенин Н. В. Курс теоретической механики. / Н. В. Бутенин, Я. Л. Лунц,. – М.: Физматгиз, 1970. 4. Бать М. И., Теоретическая механика в примерах и задачах / М. И. Бать., Г. Ю Джанелидзе., А. С. Кельзон: – М.: Физматгиз, 2013. 5. Добронравов В. В. Курс теоретической механики / В. В Добронравов., Н. Н. Никитин – М.: Высшая школа, 1983.
Оглавление Введение ………… Расчетно-графическая работа №1……. Пример выполнения расчетно-графической работы № 1……. Расчетно-графическая работа № 2……. Пример выполнения расчетно-графической работы № 2…… Рекомендуемая литература……
Учебное издание
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Методические указания к заданиям по выполнению курсовых работ и примеры их выполнения
(СТАТИКА)
Составители: Колосов Владислав Петрович. Подбелло Александр Михайлович.
Редактор В.А. Преснова. Корректор М. А. Молчанова. Компьютерная верстка И.А. Яблоковой
Подписано к печати Формат Бум. Офсетная. Усл. печ. Тираж Заказ Санкт-Петербургский государственный архитектурно – строительный университет
190005, Санкт-Петербург, 2-я Красноармейская ул., д.4. Отпечатано на ризографе.190005, 2-я Красноармейская ул., д.5.
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
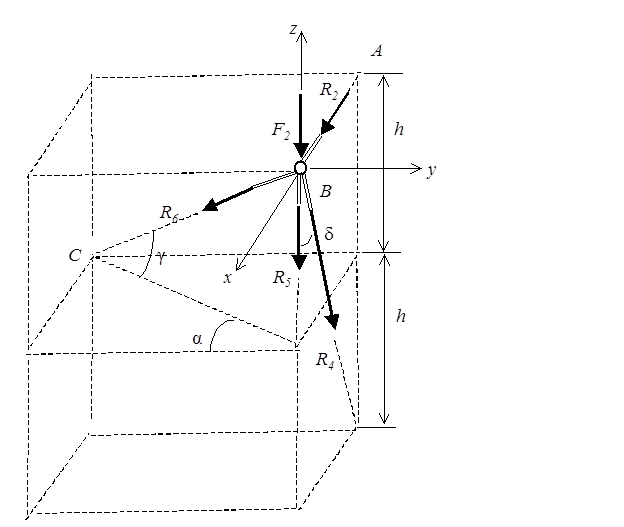
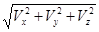= 4,2 кН
= 12,9 кНм