
|
|
Принцип максимума ПонтрягинаО Г Л А В Л Е Н И Е
ВВЕДЕНИЕ 1. ОБЗОР МАТЕМАТИЧЕСКИХ МЕТОДОВ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДВИЖЕНИЕМ ПОЕЗДА 1.1. Постановка задачи 1.2. Принцип максимума Понтрягина 1.3. Вариационное исчисление 2. ТЯГОВЫЕ СВОЙСТВА ЛОКОМОТИВОВ С УЧЕТОМ ЭКСПЛУАТАЦИОННЫХ УСЛОВИЙ 2.1. Расчетные характеристики локомотивов 2.2. Снижение коэффициента сцепления локомотивов в кривых малого радиуса 2.3. Влияние атмосферных условий на силу тяги тепловозов 3. СОПРОТИВЛЕНИЕ ДВИЖЕНИЮ ПОДВИЖНОГО СОСТАВА 3.1. Общие сведения 3.2. Основное сопротивление движению 3.3. Дополнительное удельное сопротивление движению от уклона (подъёма или спуска) 3.4. Дополнительное сопротивление от кривой 3.5. Дополнительное сопротивление от низкой температуры окружающего воздуха (ниже – 25 3.6. Дополнительное сопротивление от ветра 3.7. Сопротивление поезда при трогании с места и в начальный период движения 4. РАСЧЕТ МАССЫ СОСТАВА ГРУЗОВОГО ПОЕЗДА В УСЛОВИЯХ ЭКСПЛУАТАЦИИ 4.1. Общие положения 4.2. Выбор расчетного подъема 4.3. Расчет массы состава при движении поезда по расчетному подъему с равномерной скоростью 4.4. Расчет массы состава с использованием кинетической энергии поезда (метод подбора) 4.5. Проверка массы состава по длине приемоотправочных путей 4.6. Расчет массы состава по погонной массе 4.7. Особенности расчета для поездов повышенной массы и длины 4.8. Определение массы состава по условиям удержания поезда на уклоне вспомогательным тормозом локомотива 4.9. Построение тонно-километровой диаграммы СПИСОК ЛИТЕРАТУРЫ ВВЕДЕНИЕ
Одним из важнейших факторов, влияющих на расход топлива и электрической энергии на тягу поездов, является правильное управление локомотивом при ведении поезда. Совершенствование методов вождения поезда позволяет существенно и в короткие сроки снизить расход энергоресурсов. После обучения машинистов экономичному вождению поездов расход может быть сокращен на 10 %. Для разработки экономичных режимов управления локомотивом необходимо иметь четкое представление о математических методах оптимального управления движением и возможностях их применения для расчета программ управления локомотивом. Задача определения оптимального управления движущимся объектом, как правило, решается вариационными методами, которые разделяются на классические вариационные методы, основы которых были разработаны еще в XVIII веке Эйлером и Лагранжем, и новейшие методы, разработанные в последние годы, - динамическое программирование Р.Беллмана и “принцип максимума” Л.С.Понтрягина [ 1 ]. При оптимизации управления движением локомотива можно стремиться к достижению различных целей (критериев оптимальности), и в зависимости от этих целей, рассматривать различные задачи оптимального управления. Одним из критериев оптимального управления, который часто выступает на первый план, является критерий минимума времени достижения пункта назначения. Управление, оптимальное по этому критерию, называют оптимальным по быстродействию. Такое управление обеспечивает наибольшую провозную способность. По этому критерию производят тяговые расчеты в вычислительных центрах дорог. Другим критерием является минимизация общих расходов на перевозки, когда известно расписание движения поездов. Суммарные расходы складываются из расходов на амортизацию подвижного состава, потерь на отвлечение груза из оборота на время его транспортировки, зарплаты и расходов на топливо или электроэнергию на тягу. Если время движения задано, то оно определяет составляющие всех расходов, кроме расхода энергоресурсов на тягу. Расход топлива зависит не только от времени движения, но и от закона регулирования скорости на участках движения поезда. Минимизируя расходы на топливо при заданном времени хода, мы минимизируем тем самым и суммарные издержки. Следует отметить, что управление, оптимальное по критерию минимума суммарных расходов, критерию быстродействия или другим критериям, должно удовлетворять ограничениям по уровню мощности силовой установки, максимальной скорости движения и т.п. ОБЗОР МАТЕМАТИЧЕСКИХ МЕТОДОВ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДВИЖЕНИЕМ ПОЕЗДА Постановка задачи
Задачу определения оптимального управления движением локомотива при заданном времени хода и минимальном расходе топлива или электроэнергии можно сформулировать следующим образом. Уравнение движения поезда при условии, что масса поезда сосредоточена в центре его тяжести, описывается дифференциальным уравнением
или, если принять v = ds/dt, то уравнение примет вид
где v – скорость; t – время; s – путь; z – коэффициент; fк – удельная сила тяги; wo – основное удельное сопротивление движению поезда; u – позиция контроллера машиниста; i – сопротивление от плана и профиля пути. Требуется найти такое управление, при котором достигается минимум расхода энергоресурсов Е, то есть Е =
где Т – фиксированное время хода; G – расход энергоресурсов в единицу времени. При этом должны соблюдаться следующие ограничения: 1) 0 2) 3) v при наличии связи P =
где P – мощность локомотива; В настоящее время разработано несколько математических методов решения задач оптимального управления движущимся объектом. Рассмотрим основные из них Принцип максимума Понтрягина
Этот метод, разработанный академиком Л.С.Понтрягиным [ 1 ], при снятии ограничений 2-го и 3-го типа (по скорости и ускорению) и с учетом того, что i(s) = 0, позволяет получить аналитическое решение задачи. Рассмотрим эту задачу на примере тепловозной тяги [ 2 ]. Основное сопротивление движению поезда для заданного подвижного состава зависит только от скорости и определяется выражением
С достаточной степенью точности можно считать, что интенсивность расхода топлива линейно зависит от используемой мощности локомотива
Е = где Обозначив s = x, v =
Для удобства записи производные обозначены здесь точками. Для применения принципа максимума Понтрягина, приняв x = x1 и
Необходимо найти такое управление u(t), которое перевело бы систему (1.8) из начального состояния x1(0) = x10 и х2(0) = x20 в конечное x1(Т) = 0 и x2(Т) = 0, обеспечивая при этом минимум функционала (1.3). Функция Гамильтона [ 1 ] для системы (1.8) запишется в виде
Н( где
Подставляя значения Н(
Для оптимальности процесса необходимо, чтобы выполнялось условие максимума:
Н(
Как следует из уравнения (1.11) функция Н достигает максимума при u(t) равной umax, если u = (1.13) 0, если Отсюда следует, что оптимальное по расходу топлива управление является кусочно-постоянной функцией, принимающей значения umax или 0 (рис.1.1).
Рис. 1.1 График оптимального по расходу топлива управления тепловозом при отсутствии уклонов
Для определения скорости и момента отключения тяговых двигателей произведем следующие действия. Запишем уравнения для функции yi, используя уравнение (1.10):
Из выражения (1.14)
Функция При u = 0; [
t =
При u = umax; [0,
t =
t =
В момент
Из выражения (1.18) находится скорость переключения Процесс, оптимальный по расходу топлива при фиксированном времени хода Т, приведен на рис.1.2. В момент t = 0 включается тяга u = umax для осуществления разгона. При достижении времени
Вариационное исчисление
Вариационные методы позволяют определять функции, доставляющие экстремум (максимум или минимум) различным функционалам. Основным объектом изучения в вариационном исчислении является функционал “стандартного” вида J =
то есть определенный интеграл, зависящий от независимой переменной х, искомой функции у(х) и ее производной В настоящее время имеется много информации, посвященной вариационным методам. Студент, интересующийся строгими доказательствами, а также желающий получить более обширные знания в области вариационных методов, может непосредственно обратиться к списку литературы, приведенному в конце пособия [3-5 ]. Центральной теоремой вариационного исчисления является теорема Эйлера, дающая необходимое условие того, что функция у(х) доставляет экстремум функционалу (1.19) с граничными условиями у(а) = уа, у(b) = уb среди всех гладких (имеющих непрерывную первую производную Функционал (1.19) достигает экстремума , если функция у(х) является решением уравнения Эйлера (выведенного в 1744 году): Fy -
где Чтобы раскрыть смысл уравнения Эйлера, произведем дифференцирование по х второго члена уравнения (1.20):
Таким образом, уравнение Эйлера является нелинейным дифференциальным уравнением второго порядка. Смысл уравнения Эйлера заключается в том, что задачу определения функции, доставляющей экстремум функционалу (1.19), оно сводит к хорошо известной задаче интегрирования дифференциального уравнения. Кривые, удовлетворяющие уравнению Эйлера, называются э к с т р е м а л я м и. В связи с этим основная теорема вариационного исчисления имеет следующую формулировку: если экстремум функционала вида (1.19) существует и достигается среди гладких функций, то он может достигаться только на экстремалях. Для функционала, зависящего от второй производной, необходимым условием экстремума является выполнение уравнения Эйлера – Пуассона
представляющего собой дифференциальное уравнение четвертого порядка. Сложность решения задачи, поставленной в подразделе 1.1, заключается в том, что для обеспечения минимума расхода топлива необходимо учитывать характеристики всех элементов сложной силовой установки тепловоза: дизеля, электрического генератора, тяговых двигателей, а также законы сопротивления движению подвижного состава. Если исходить только из характеристик первичного двигателя – дизеля, то оптимальным будет такое управление, при котором поддерживается постоянная мощность дизеля. С помощью вариационного исчисления можно решить эту задачу при следующих допущениях: – к.п.д. передачи тепловоза в процессе движения не меняется; – расход топлива дизелем зависит от мощности линейно по формуле (1.6). Используя формулы (1.1), (1.6) и (1.7), запишем уравнение движения поезда в виде Тогда расход топлива E на прохождение перегона длиной So за время Т будет равен интегралу Е = где s – путь, Для определения оптимального закона управления достаточно найти функцию s(t), доставляющую минимум функционалу J = Уравнение Эйлера - Пуассона для функционала (1.24) имеет вид то есть распадается на два уравнения Таким образом, оптимальным по расходу топлива является режим с постоянной скоростью движения тепловоза. Если уклон не является постоянным (i(s) Следовательно, если для дизеля, взятого изолированно, оптимальным является поддержание постоянной мощности, равной номинальной, то при учете всех факторов оптимальным режимом является режим поддержания постоянной скорости.
Если сопротивление движению подвижного состава i(s) постоянно, либо меняется в незначительных пределах (уклоны не являются крутыми), то общая структура оптимального режима движения по перегону непосредственно следует из обобщенной теоремы Эйлера: в начальный момент времени, после трогания с места, определяющим является ограничение по максимальному ускорению и осуществление режима По мере роста скорости увеличивается и мощность , забираемая от дизеля, и когда эта мощность становится равной максимальной, происходит переход на режим Р = Pmax (участок АВ на рис.1.3). Как только скорость достигнет значения v0, осуществляется переход на частичное использование мощности к движению по экстремали Величина скорости v0 на участке экстремали выбирается такой, чтобы, с учетом неизбежных участков равнялась бы заданному значению v ср = 1/ T, то есть площади so, ограниченной кривой 0ABCDF (рис.1.3). Рассмотрим теперь структуру оптимального управления при наличии крутых подъемов . Если i(s) велико, то неизбежен провал скорости, и для того, чтобы сохранить прежнее значение интеграла (1.26) нужно увеличить скорость на других участках. Пусть новая скорость тепловоза будет равна v1 = v0 + Тогда можно записать
Наименьшее значение интеграла (1.27) будет в том случае, когда функция e (t) станет по возможности симметричной, то есть повышение скорости перед крутым подъемом равно снижению скорости вследствие движения по уклону.
Таким образом, оптимальной оказывается следующая структура движения: перед крутым подъемом переходят на режим Р = Pmax,увеличивая скорость на величину D v (по отношению к v0), равную половине снижения скорости при движении на подъеме (рис.1.4). Техническая реализация оптимального управления тепловозом следующая. Величиной, которая должна быть известна перед началом движения, является скорость v0 на участках экстремали. Эта скорость определяется путем тягового расчета для заданной массы состава из такого условия, чтобы, с учетом участков разгона и торможения, а также падения скорости на крутых подъемах, средняя скорость движения по перегону в целом равнялась заданной.
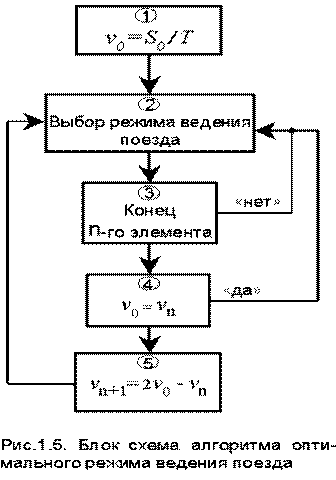
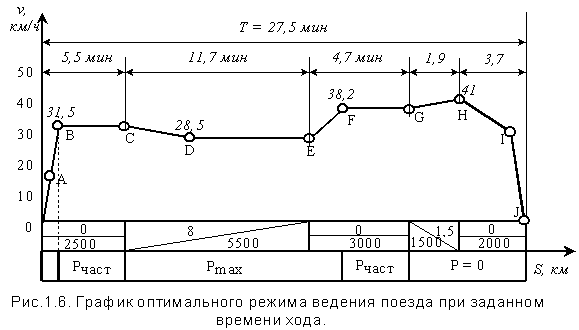
Так как скорость v0 вычисляется для расчетной массы состава, которая может отличаться от действительной, а реальная величина сил сопротивления может отличаться от расчетных, то при рассчитанном заранее значении v0 может оказаться невозможным выполнение заданного время хода. Однако ошибки в расчете v0, вызванные неполнотой и неточностью имеющейся информации о массе состава и силах сопротивления движению, могут быть легко исправлены корректировкой. Алгоритм программы для ЭВМ, реализующий такую корректировку рассматривался автором в работах [ 6-8 ]. Упрощенная блок-схема алгоритма приведена на рис.1.5. Блок 1 вычисляет среднюю скорость v0 на участках экстремали. Блок 2 , в зависимости от скорость v0 и профиля пути i(s), определяет необходимую мощность (позицию контроллера машиниста) для поддержания скорости v0. Блок 3 определяет границу n-го элемента профиля пути или перегона. Блок 4 сравнивает заданную скорость движения с действительной средней скоростью на n-м элементе. Если скорость v0 не равна скорости vn, то блок 5 производит корректировку средней скорости для следующего перегона и т.д. Таким образом, несмотря на то, что на некоторых перегонах средняя скорость может оказаться меньше заданной, график движения по всему участку будет выполнен. Рассмотрим на конкретном примере разработку оптимального режима ведения поезда тепловозом на перегоне длиной s0 =14,5 км и заданном времени хода T = 27,5 мин (рис.1.6). Кривую скорости и время хода строим с помощью тяговых расчетов.
1. Определяем среднюю скорость на перегоне v0= s0 / T = 14,5 / 0,46 = 31,5 км/ч.
2. Разгоняем поезд до средней скорости 31,5 км/ч, используя сначала частичную, а потом максимальную силу тяги (участок 0AB). Затем до конца первого элемента профиля пути следуем с равномерной (средней) скоростью (линия ВС), используя частичную силу тяги. В конце первого элемента пути поезд имеет скорость 31,5 км/ч и время хода до точки С 3. Корректируем среднюю скорость движения поезда для оставшейся части перегона s1 = s0 - vср2 = 12 / 0,37
4. Имея начальную скорость для 2-го элемента (i2 = 8 ‰ ) 31,5 км/ч и конечную 28 км/ч, поезд пройдет этот участок, используя максимальную силу тяги за время 5. Корректируем среднюю скорость движения поезда для оставшейся части перегона s2 = 14,5 - 2,5 - 5,5 = 6,5 км ; t2 = 27,5 - 5,5 - 11,7 = 10,3 мин ( 0,17 ч); vср3= s2 / t2 = 6,5 / 0,17 = 38,2 км/ч.
6. В начале третьего элемента (i3= 0 ‰ , D S3 = 3000 м) реализуется максимальная сила тяги до скорости 38,2 км/ч (отрезок ЕF), а затем до конца элемента сохраняется постоянная скорость. При этом используется частичная сила тяги локомотива. Этот элемент поезд проследует за 7. Находим среднюю скорость для оставшейся части перегона s3 = 14,5 - 2,5 - 5,5 - 3 = 3,5 км; t3 = 27,5 - 5,5 - 11,7 - 4,7 = 5,6 мин (0,093 ч); vср3= s3 / t3 = 3,5 / 0,093 = 37,6 км/ч.
8. Скорость на четвертом элементе (i4 = -1,5 ‰ , 9. Длина оставшейся части перегона Для того чтобы этот участок был пройден со средней скоростью vср5= s5 / t5 = 3,5 / 0,093 = 37,6 км/ч = 33,3 км/ч
поезд должен следовать в режиме холостого хода на отрезке HI, а затем в режиме служебного торможения на отрезке IJ.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 )
) = z [ fк(v,u) - w o(v) - i(s)] (1.1)
= z [ fк(v,u) - w o(v) - i(s)] (1.1) = z [ fк(v,u) - w o(v) - i(s)]
= z [ fк(v,u) - w o(v) - i(s)]  , (1.2)
, (1.2)
 min, (1.3)
min, (1.3) F
F 
 , (1.4)
, (1.4)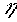 – к.п.д. передачи локомотива.
– к.п.д. передачи локомотива.  . (1.5)
. (1.5)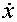 ,
,  , с учетом формул (1.1) - (1.6) и рационального выбора единиц измерения, запишем уравнение движения поезда в безразмерном виде
, с учетом формул (1.1) - (1.6) и рационального выбора единиц измерения, запишем уравнение движения поезда в безразмерном виде - к0 - к1
- к0 - к1  - к2
- к2  (1.8)
(1.8)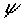 , x, u) =
, x, u) =  . (1.10)
. (1.10) ). (1.11)
). (1.11)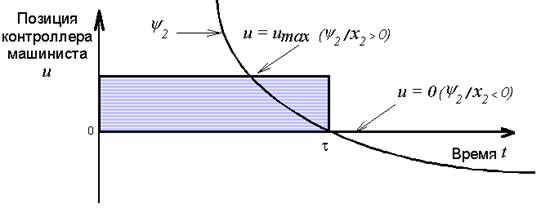
 =
=  = 0;
= 0; 2 =
2 =  )
)  =
=  - к0 - к1 х2- к2
- к0 - к1 х2- к2 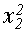 ;
; 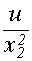 )
)  ] и [
] и [ 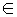 [
[  = - к0 - к1х2 - к2
= - к0 - к1х2 - к2  ; -
; - 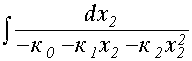 =
=  dt ;
dt ; 1(x2) + С2;x2(T) = 0; С2 = T -
1(x2) + С2;x2(T) = 0; С2 = T -  ;
; ;
;  (1.18)
(1.18)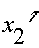 в момент
в момент 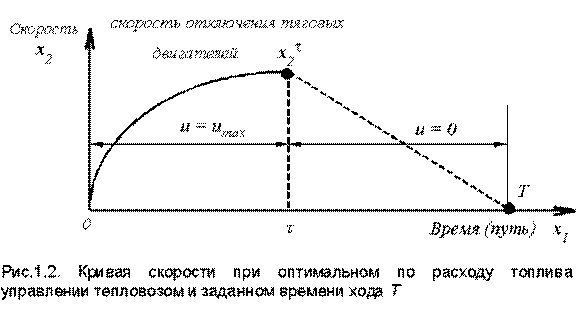
 , (1.19)
, (1.19) .
. , (1.20)
, (1.20) ;
;  .
. . (1.21)
. (1.21)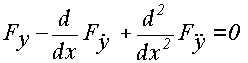 , (1.22)
, (1.22) (
(  + к0 + к1+ к2
+ к0 + к1+ к2  =
= 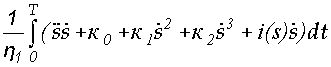 , (1.23)
, (1.23) – ускорение.
– ускорение. . (1.24)
. (1.24) ) = 0, откуда следует, что
) = 0, откуда следует, что  const), то постоянство скорости движения может быть достигнуто с помощью регулирования мощности дизеля.
const), то постоянство скорости движения может быть достигнуто с помощью регулирования мощности дизеля.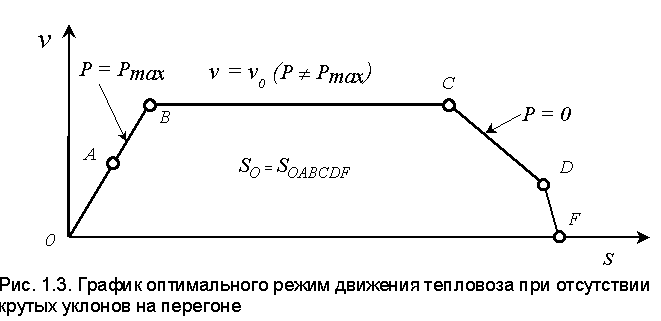
 = v0. Движение по экстремали продолжается почти до конца перегона (участок ВС на рис.1.3), перед концом движения происходит свободный выбег состава (движение по границе допустимой области Р = 0 - участок CD на рис.1.3), и в самом конце - торможение механическим тормозом.
= v0. Движение по экстремали продолжается почти до конца перегона (участок ВС на рис.1.3), перед концом движения происходит свободный выбег состава (движение по границе допустимой области Р = 0 - участок CD на рис.1.3), и в самом конце - торможение механическим тормозом.
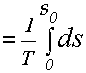 (1.26)
(1.26) .
. . (1.27)
. (1.27)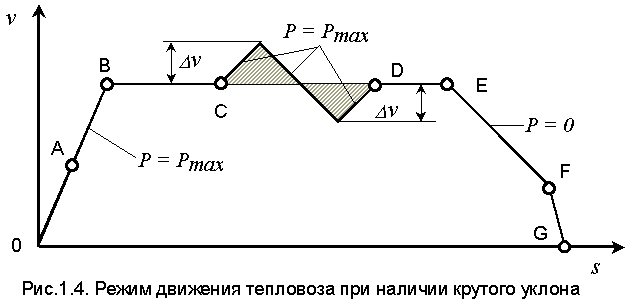
 t1 = 5,5 мин.
t1 = 5,5 мин.  32,4 км/ч.
32,4 км/ч.