Теория по теме «Рациональные уравнения»

не корень (не кратный корень)

корень (кратности 2)

Решение.

1-й способ.
Определим, сколько роз можно купить на 550 рублей. Для этого разделим с остатком 550 (деньги Сергея) на 45 (цена розы).

550 : 45 = 12 (ост. 10). Денег у Сергея хватит на 12 роз и 10 рублей останется. Но букет из 12 роз нам не подходит! Нужно нечётное число роз. Наибольшее подходящее число — это 11.

Ответ: 11

2-й способ.
10 роз стоят 450 рублей, при этом у Сергея останется 100 рублей. На 100 рублей можно купить не более двух роз. Поэтому всего можно купить не больше 12 роз. Число 12 — чётное, не подходит по условию. Значит, наибольшее количество роз в букете — это 11.

Ответ: 11

2. В пачке бумаги 250 листов формата A4. За месяц в школе используется 1200 листов. Какое наименьшее число пачек бумаги нужно купить в школу на 3 месяца?

Решение.
За месяц в школе используется 1200 листов бумаги, поэтому за 3 месяца израсходуют 1200 · 3 = 3600 листов. В каждой пачке 250 листов, поэтому необходимо 3600 : 250 = 14,4 пачек. Ясно, что дробное число пачек никто продавать не станет, поэтому придётся купить 15 пачек бумаги.

Ответ: 15

3. Маша купила месячный проездной билет на троллейбус. Проездной билет стоит 280 рублей, а разовая поездка — 7 рублей. Сколько рублей сэкономила Маша, если за месяц она сделала 48 поездок на троллейбусе?

Решение.
Одна разовая поездка стоит 7 рублей, поэтому 48 разовых поездок стоят 48 · 7 = 336 рублей. Купив проездной за 280 рублей, Маша сэкономила 336 − 280 = 56 рублей.

Ответ: 56

Задачи с решениями

Задача 1

Дневник стоит 60 рублей. Какое наибольшее число дневников можно будет купить на 550 рублей после понижения цены на 20%?

Решение

Определим размер скидки в рублях:
60*0,2=12 рублей
Цена дневника после скидки:
60-12=48 рублей
Определим, сколько дневников можно купить на 550 рублей:
550/48=11 дневников и 22 рубля сдачи.

Ответ:11

Задача 2

Майка стоит 180 рублей. Какое наибольшее число маек можно купить на 600 рублей во время распродажи, когда скидка составляет 20%?

Решение

Определим размер скидки на майку в рублях

180*0,2=36 рублей

Определим цену майки с учетом скидки

180-36=144 рубля

Определим, сколько маек можно купить на 600 рублей в период распродажи

600/144=4 майки и еще останется 24 рубля на мороженое

Ответ:4

Теория по теме «Проценты»

1. Платье стоит 2120 рублей. Скидка в день распродажи равна 35%. Сколько стоит платье со скидкой в день распродажи?
Решение.
1-й способ.
Стоимость платья без скидки составляет 100%, поэтому 1% равен 2120 : 100 = 21,2 рубля. Скидка составляет 35%, то есть 21,2 · 35 = 742 рубля. Цена платья со скидкой равна 2120 − 742 = 1378 рублей.
Ответ: 1378.
2-й способ.
Стоимость платья без скидки составляет 100%, скидка равна 35%. Стоимость платья со скидкой составляет 100% − 35% = 65% от цены без скидки. Найдём 65% от 2120 рублей. Чтобы найти проценты от числа, нужно это число разделить на 100 и умножить на число процентов. 2120 : 100 · 65 = 1378 рублей.
Ответ: 1378.
2.Билет на междугородный автобус для взрослого стоит 260 рублей. Стоимость билета для ребёнка до 10 лет составляет 50% от стоимости билета для взрослого. Группа состоит из 17 детей до 10 лет и 2 взрослых. Сколько рублей стоят билеты на всю группу?
Решение.
Стоимость билета для ребёнка составляет 50% от 260 рублей, то есть 260 : 100 · 50 = 130 рублей. 17 детских билетов по 130 рублей стоят 130 · 17 = 2210 рублей. 2 взрослых билета по 260 рублей стоят 260 · 2 = 520 рублей. Билеты на всю группу стоят 2210 + 520 = 2730 рублей.
Ответ: 2730

Задачи с решениями

Задача 1

Подоходный налог составляет 13% от заработной платы. Заработная плата почтальона составляет 7800 рублей. Сколько рублей получит почтальон после удержания налога?

Решение

Если подоходный налог составляет 13%, то почтальон получит 100-13=87% от своей ставки. Теперь определим сколько денег получит почтальон:

7800*0,87=6786

Ответ:6786

Задача 2

Оптовая цена ножа 160 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких ножей можно купить по розничной цене на 3000 рублей?

Решение

Определим, на сколько розничная цена дороже оптовой:

160*0,2=32 рубля

Найдем розничную цену:

160+32=192 рубля

Определим, сколько ножей можно купить на 3000 рублей:

3000/192=15 ножей и 120 рублей сдачи

Ответ:15

Теория по теме «Графики»

Графики и диаграммы характеризуют изменение некоторой величины (температуры, количества осадков, стоимости акций и т.п.) от времени. В задачах данного раздела нужно, как правило, найти:

наибольшее или наименьшее значение этой величины;
разность между наибольшим и наименьшим значениями;
момент времени, когда величина примет какое-то значение;
ответ на другой, подобный этим, вопрос.

Главное при решении подобной задачи — внимательно прочитать условие и вопрос. При поиске ответа на этот вопрос надо прямо на графике провести недостающие линии, при необходимости дописать пропущенные числа.
Иногда в этих заданиях употребляются разные фразы, обозначающие одно и то же, например: «На рисунке показано изменение дневной температуры воздуха на протяжении первых трех недель мая» или «На рисунке показано изменение температуры воздуха на протяжении первой и второй декад мая».

Декада — это 10 дней.
Полдень — 12:00,
Полночь — 24:00 или 00:00,
Квартал — 3 месяца.

Задачи с решениями

Попробуем по одному и тому же графику решить несколько задач.

1. На графике (см. рис) показано изменение температуры воздуха в некотором населённом пункте на протяжении трёх суток, начиная с 0:00 часов четверга.

На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах Цельсия.

a) Определите по графику наименьшую температуру воздуха в ночь с пятницы на субботу (ночь длится с 19:00 до 5:00). Ответ дайте в градусах Цельсия.
б) Определите по рисунку разность между наибольшим и наименьшим значениями температуры воздуха в четверг.

Решение.

a)Прочитаем ещё раз задание: «Определите по графику наименьшую температуру воздуха в ночь с пятницы на субботу». На графике (см. рис. ниже) отметим нужный промежуток времени (ночь с пятницы на субботу). Видим, что ответ — 14 градусов.

Ответ: 14

б)Прочитаем ещё раз задание: «Определите по рисунку разность между наибольшим и наименьшим значениями температуры воздуха в четверг». На графике (см. рис. ниже) выделяем временной промежуток — четверг. Находим наименьшее значение 9 и наибольшее 20. Находим разность 20 − 9 = 11.

Ответ: 11

Рассмотрим теперь пример задачи с диаграммой. Отличие этих задач заключается только в форме представления данных нарисунке. Решения этих задач абсолютно аналогичны.

2. На диаграмме (см. рис) показана среднемесячная температура воздуха в городе N за каждый месяц 1965 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в период с января по сентябрь 1965 года включительно.

Решение.

Мы знаем, что январь — 1-й месяц года, а сентябрь — 9-й. Тогда по диаграмме видно, что с 1-го по 9-й месяц наименьшая среднемесячная температура была −10 градусов Цельсия.

Ответ: −10

Задачи с решениями

Задача 1

На графике (см. рис.) представлено изменение биржевой стоимости акций энергетической компании за 3 дня июня. По оси абсцисс отложено время в часах, по оси ординат — стоимость одной акции в рублях. Определите по графику наименьшую цену акции за 24 июня.

Решение

Самая низкая цена акций 24го июня была ровно посередине между 3130 и 3150. Значит минимальная цена акции в этот день 3140 рублей.

Ответ:3140

Задача 2

На графике (см. рис.) представлено изменение биржевой стоимости акций угледобывающей компании с утра 23 июня по вечер 25 июня 2010 года. По оси абсцисс отложено время, по оси ординат — стоимость одной акции в рублях. Определите по графику, какого числа цена акции первый раз упала ниже1138 рублей. Рабочий день биржи начинается в 10:30.

Решение

23 июня в первый раз цена опустилась ниже 1138 рублей за акцию.

Ответ:23

Теория по теме «Диаграммы»

наибольшее или наименьшее значение этой величины;
разность между наибольшим и наименьшим значениями;
момент времени, когда величина примет какое-то значение;
ответ на другой, подобный этим, вопрос.

Декада — это 10 дней.
Полдень — 12:00,
Полночь — 24:00 или 00:00,
Квартал — 3 месяца.

Задачи с решениями

Попробуем по одному и тому же графику решить несколько задач.

На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах Цельсия.

Решение.

Ответ: 14

Ответ: 11

Решение.

Ответ: −10

Задачи с решениями

Задача 1

На диаграмме (см. рис.) показана среднемесячная температура воздуха в городе N за каждый месяц 1984 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в период с марта по декабрь 1984 года включительно.

Решение

Март – третий месяц, декабрь – двенадцатый. В этом диапазоне холоднее всего было в 12 месяце (декабре), средняя температура достигла значения -10 градусов

Ответ:-10

Задача 2

Определите по рисунку, какое наибольшее количество миллиметров осадков выпало в период с 5 по 12 сентября.

Решение

Из рисунка определим, сколько осадков выпадало в каждый из дней с 5го по 12 сентября:
5го 2 мм, 6го 0 мм, 7го 2 мм, 8го 0 мм, 9го 3 мм, 10го 0 мм, 11го 0 мм и 12го 4 мм.

Больше всего с 5 по 12 сентября выпало 12 сентября, 4 мм.

Ответ:4

Теория по теме «Векторы»

Отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом, называется вектором.
Вектор характеризуется модулем (длиной отрезка) и направлением. Два вектора, имеющие одинаковые модули и направления, равны.
Вектор с началом в точке A и концом в точке B обозначают ➛AB или строчной (маленькой) буквой, например ➛a (см. рис. 222).

Модуль (длину) вектора обозначают | ➛AB|.
Сумма векторов — это вектор, который можно получить двумя способами (см. рис. 223). Заметим, что для любых точек A, B и C

Разность векторов тоже можно получить двумя способами:

Координаты и векторы в пространстве
1. Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.

4. Любой вектор можно единственным образом разложить по трём некомпланарным векторам.

9. Координаты середины отрезка равны средним арифметическим координат его концов.
10. Свойства скалярного произведения векторов:

Задачи с решениями

Стороны правильного треугольника KNP равны 10 (см. рис. 225). Найдите длину вектора

Решение.

Ответ: 10.
Стороны правильного треугольника KNP равны 10 (см. рис. 226). Найдите квадрат длины вектора

Решение.

Ответ: 10.

Теория по теме «Линейные, квадратные, кубические уравнения»

Линейные уравнения

Линейные уравнения — это уравнения вида ax = b, где неизвестным является x, а буквы a и b обозначают заданные числа.
Если a = 0, то либо уравнение не имеет корней (как, например, уравнение 0x = 7), либо x может быть любым числом (если 0x = 0). При a <> 0 корень уравнения находят по формуле:
x = b : a
Задачи с решениями
Найдите корень уравнения −5x = 3.
Решение.
Разделим обе части уравнения на −5.
x = 3 : (−5); x = −0,6 — корень заданного уравнения.
Ответ: −0,6.

Квадратные уравнения

Квадратные уравнения — это уравнения вида ax² + bx + c = 0, где a 6= 0.
Основная формула для решения квадратного уравнения:

Задачи с решениями
Решите уравнение 3x² + 4x − 207 = 0. Если корней более одного, в ответ запишите меньший корень.
Решение.
3x² + 4x − 207 = 0. Для данного уравнения a = 3, b = 4 и c = −207. Подставим эти значения в формулу для нахождения корней квадратного уравнения:

Ответ: −9.
Квадратный трёхчлен
Квадратный трёхчлен — это многочлен степени 2:

Если x₁, x₂ — корни f(x), то

Если второй коэффициент делится на 2, то есть f(x) = ax² + 2kx + c, то

Если старший коэффициент равен 1, то есть f(x) = x² + px + q, то

Выражение b² − 4ac называется дискриминантом соответствующего многочлена f(x) (уравнения f(x) = 0). Дискриминант принято обозначать большой буквой D. Отметим, что

*Теорема Безу и схема Горнера
Для любого многочлена степени n > 0

и любого числа x₀ ∈ R найдётся такой многочлен степени n − 1

что справедливо равенство

причём коэффициенты q(x) могут быть вычислены по следующему алгоритму:

Результаты вычисления коэффициентов многочлена q(x) удобно помещать в таблицу (схему Горнера).

	a_n	a_n-1	a_n-2	...	a_i+1	a_i	...	a₂	a₁	a₀
x₀	b_n-1	b_n-2	b_n-3	...	b_i	b_i-1	...	b₁	b₀	f(x₀)

Понятно, что если x₀ — корень многочлена f(x), то f(x₀) = 0 и, следовательно,
f(x) = (x−x₀)q(x) (следствие из теоремы Безу).
Таким образом, чтобы выяснить, является ли число x₀ корнем многочлена f(x), нужно заполнить приведённую выше таблицу (схему Горнера). Если f(x₀) окажется равным 0, то x₀ — корень. В противном случае x₀ — не корень f(x)
Приведём ещё одну теорему о многочленах и следствие из неё, касающееся рациональных корней многочлена.
Теорема. Пусть f(x) = a_nx⁰ + a_n-1x^n-1 + . . . + a₁x + a₀ — многочлен с целыми коэффициентами. Если несократимая дробь (рациональное число) p/q является корнем многочлена f(x), то

Следствие. Пусть f(x) = a_nx⁰ + a_n-1x^n-1 + . . . + a₁x + a₀ — многочлен с целыми коэффициентами. Тогда все рациональные корни многочлена f(x)являются целыми и являются делителями свободного члена a₀.
Эти теоремы будут очень полезными при выполнении некоторых заданий, их использование существенно сэкономит время решения.

x⁴ + 3x³ + x² − 3x − 2 = (x − 1)(x + 1)²(x + 2)
Данное уравнение имеет 3 корня: 1; −1; −2, причём −1 — корень кратности 2.

Пример 2. Решите уравнение 6x⁴ + 17x³ + 20x² + 14x+ 3 = 0.
Решение. По теореме все рациональные корни уравнения находятся среди чисел

Видим, что корнями могут быть лишь отрицательные числа. Поэтому проверяем числа

Корнями могут быть лишь отрицательные числа, причём −1 и −1/2 не являются корнями (проверили выше).
Проверяем числа −3; -3/2.

Теория по теме «Рациональные уравнения»

Понятие уравнения

Дробно-рациональные уравнения

Задачи с решениями

Так как дроби c одинаковым знаменателем равны, то их числители тоже должны быть равны:

При x = −2 знаменатель 3x + 4 не равен нулю, значит, это корень исходного уравнения.
Ответ: −2.

Решение.
Превратим это уравнение в пропорцию — равенство двух дробей:

В пропорции произведение крайних членов равно произведению средних (если говорить образным языком, «умножаем крест-накрест»):

Ответ: −3.

Теория по теме «Иррациональные уравнения»

Понятие уравнения

Иррациональные уравнения

При решении иррациональных уравнений нам приходится возводить обе части уравнения в квадрат. Нужно помнить, что квадратный корень не может быть отрицательным. Если в уравнении квадратный корень равен выражению, которое может быть отрицательным, необходимо делать проверку

Задачи с решениями

Решение.
Возведём обе части уравнения в квадрат

Ответ: 17.
В этом уравнении проверка не нужна, но гораздо проще проверить получившийся ответ, чем понять, нужна проверка или нет. Кроме того, проверка позволяет понять, не сделаны ли были ошибки в вычислениях во время решения уравнения.

Ответ: −7

Задачи с решениями

Задача 1

Найдите корень уравнения √38−11x=4.

Решение

Обе части возведем в квадрат:

38-11x=16

11x=38-16

11x=22

X=2

Ответ:2

Теория по теме «Показательные уравнения»

Понятие уравнения

Показательные уравнения

Самые простые показательные уравнения решают приведением обеих частей уравнения к одному основанию: a^x = a^y, откуда получают x = y

Задачи с решениями

Ответ: 27

Ответ: -3

Теория по теме «Операции со степенями»

Определение степени и корня
1. Пусть a ∈ R, n ∈ N. Тогда

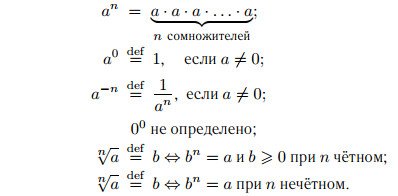
2. Пусть a ∈ R⁺ ; m ∈ Z, n ∈ N, n > 1. Тогда

Правила действий с радикалами
Пусть m, n, k ∈ N, m, n > 1; a, b ∈ R⁺. Тогда

Правила действий со степенями
Пусть p, q ∈ Q, a, b ∈ R⁺. Тогда

Не приводя определения степени с действительным показателем, от- метим, что правила действий с такими степенями «сохраняются», то есть приведённые правила верны и для p, q ∈ R

Задачи с решениями

Теория по теме «Логарифмические уравнения»

Понятие уравнения

Уравнение — это равенство, в котором содержится неизвестная величина (переменная). Напомним основные правила, с помощью которых можно решить уравнение.
• При умножении суммы на множитель каждое слагаемое умножают на этот множитель:

• При переносе слагаемого из одной части уравнения в другую перед этим слагаемым меняют знак:

• Знаки перед каждым слагаемым в уравнении можно одновременно поменять на противоположные:

• Произведение равно нулю, если хотя бы один из множителей равен нулю и все другие множители при этом имеют смысл. Например, (x + 5)(x − 2) = 0, если или x + 5 = 0, или x − 2 = 0. Отсюда получаем два корня уравнения: x = −5; x = 2
Определение логарифма
Логарифмом положительного числа x по основанию a(a > 0, a ≠ 1) называется показатель степени y, в которую нужно возвести a, чтобы получить число x:

Свойства логарифмов
Пусть a > 0, a ≠ 1.
1. Основное логарифмическое тождество:

2. Логарифм произведения, частного и степени:

3. Формула перехода к новому основанию. Пусть b > 0, b ≠ 1, x > 0. Тогда

Кроме того, log_a x log_by = log_a y log_bx.
4. Пусть b > 0, a ≠ 0, a ≠ 1, тогда

При решении задач бывает полезна следующая теорема.
Если числа a и b на числовой оси расположены по одну сторону от единицы, то log_a b > 0, а если по разные, то log_a b < 0.
Задачи с решениями

Теория по теме «Тригонометрические уравнения и преобразования»

Понятие уравнения

Радианное измерение углов
Один радиан равен центральному углу окружности, длина дуги которого равна радиусу этой окружности.

Значения тригонометрических функций некоторых углов

Основные тригонометрические тождества

Формулы суммы и разности аргументов

Формулы двойного и тройного аргументов

Выражение тригонометрических функций через тангенс половинного угла

Преобразование суммы и разности тригонометрических функций в произведение

Преобразование произведения тригонометрических функций в сумму

Определение обратных тригонометрических функций

Свойства обратных тригонометрических функций

Некоторые значения обратных тригонометрических функций

Формулы для решения простейших тригонометрических уравнений

Тригонометрические уравнения

Как правило, решение любого тригонометрического уравнения сводится к решению одного из трёх видов простейших тригонометрических уравнений: sin x = a, cos x = a или tg x = a.
Для всех тригонометрических уравнений характерно то, что мы получаем бесконечное число корней уравнения, хотя пишем при этом одно или два выражения для корней. Это происходит потому, что тригонометрические функции периодические, то есть повторяющиеся через определённый промежуток — период. То есть если у нас есть один корень, то будет и ещё бесконечно много, отличающихся друг от друга на величину, равную периоду.
В приведённых задачах требуется в ответе указать наибольший отрицательный или наименьший положительный корень. Часто при решении таких уравнений возникают формулы вида x = 1 + 4k, x = 3 + 4k, где k ∈ Z. Разберёмся, что это означает и как по этим формулам получить корни уравнения.
Запись k ∈ Z означает, что k может быть любым целым числом, то есть может принимать значения 0; 1; −1; 2; −2; . . . ; 419; −419 и так далее. Число 419 мы взяли для примера.
Подставим некоторые значения k в первую формулу:

Так можно будет получить сколь угодно много различных корней. Теперь подставим значения k во вторую формулу:

Попробуем найти наибольший отрицательный корень. Выбираем отрицательное число, которое ближе всего к нулю. Для первой формулы это −3, для второй — это −1, ближе к нулю (и больше) число −1, значит, наибольший отрицательный корень равен −1.
Теперь попробуем найти наименьший положительный корень. Выбираем положительное число, которое ближе всего к нулю. По первой формуле это 1, по второй — это 3, ближе к нулю (и меньше) число 1, значит, наименьший положительный корень равен 1.
Задачи с решениями

Немного полезной информации

Задачи с решениями

Теория по теме «Преобразование логарифмических выражений»

Логарифмические выражения

Определение логарифма
Логарифмом положительного числа x по основанию a (a > 0, a ≠ 1) называется показатель степени y, в которую нужно возвести a, чтобы получить число x:

Свойства логарифмов
Пусть a > 0, a ≠ 1.
1. Основное логарифмическое тождество:

2. Логарифм произведения, частного и степени:

3. Формула перехода к новому основанию. Пусть b > 0, b ≠ 1, x > 0. Тогда

4. Пусть b > 0, a 6= 0, a ≠ 1, тогда

Задачи с решениями

Теория по теме «Преобразование иррациональных выражений»

Действия с корнями

Вспомним основные формулы:

Задачи с решениями

Теория по теме «Преобразование рациональных выражений»

Действия с обыкновенными дробями

Вспомним, как производить простейшие вычисления с обыкновенными дробями. Чтобы перемножить дроби, нужно умножить их числители и записать результат в числитель, а потом перемножить знаменатели и результат записать в знаменатель:

Если числитель и знаменатель дроби делятся на одно и то же число, то на него обычно делят каждый из них и называют это «сократить дробь»:

Иногда сокращение выполняют во время умножения дробей:

Если дроби смешанные (с выделенной целой частью), то нужно их перевести в обыкновенные (состоящие только из числителя и знаменателя). Для этого целую часть умножают на знаменатель, прибавляют числитель и результат записывают в числитель, а знаменатель оставляют прежним:

Чтобы перевести неправильную дробь (числитель больше знаменателя) в смешанную (выделить целую часть), нужно числитель разделить на знаменатель с остатком. Тогда неполное частное будет целой частью, остаток будет числителем, а знаменатель останется тем же:

Чтобы перевести обыкновенную дробь в десятичную, надо числитель разделить на знаменатель:

Чтобы умножить обыкновенную дробь на десятичную, нужно или обыкновенную перевести в десятичную, или десятичную в обыкновенную:

Чтобы разделить число на обыкновенную дробь, нужно в этой дроби поменять местами числитель со знаменателем и умножить число на полученную дробь:

Чтобы целое число записать в виде обыкновенной дроби, нужно записать его со знаменателем 1:

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители и записать числитель новой дроби, а знаменатель оставить прежним. Чтобы вычесть дроби с одинаковыми знаменателями, нужно вычесть их числители и записать числитель новой дроби, а знаменатель оставить прежним. Если у дробей есть целая часть, то нужно сначала сложить или вычесть целые части:

Не нашли, что искали? Воспользуйтесь поиском по сайту: