
|
|
Дисперсия случайной величиныДве случайные величины могут иметь одинаковые математические ожидания, но разное рассеяние. Это значит, что математическое ожидание полностью случайную величину не характеризует. Поэтому вводится еще одна числовая характеристика, которая называется дисперсией и характеризует рассеяние случайной величины относительно математического ожидания. Дисперсией дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания
Пример. Случайная величина Х имеет распределение
Требуется вычислить дисперсию. Имеем:
На практике для вычисления дисперсии используют другую, более удобную формулу
Доказательство:
Свойства дисперсии
1. D(С)=0, т.е. дисперсия постоянной величины С равна нулю. 2. D(CX)=C2D(X) – постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат. Доказательство:
3. D(X+Y)=D(X)+D(Y) – дисперсия суммы двух независимых случайных величин равна сумме их дисперсий. Доказательство:
Так как для независимых случайных величин M(XY)=M(X)M(Y), то последнее равенство примет вид
откуда
Приведем без доказательства еще два свойства дисперсии. 4. D(C+X)=D(X). 5. D(X–Y)=D(X)+D(Y). Отметим еще одно важное свойство дисперсии. Дисперсия числа появлений события А в n независимых испытаниях равна D(X)=npq, где p - вероятность появления события А в одном испытании; q=1-p – вероятность его непоявления. Доказательство: Найдем дисперсию числа появлений события А в одном испытании
Тогда Всего n независимых испытаний, следовательно, D(X)=npq. Дисперсия имеет размерность случайной величины в квадрате. Среднее квадратическое отклонение
Если извлечь из дисперсии квадратный корень, получим среднее квадратическое отклонение (обозначается σ(Х) или S(Х))
Размерность величины Пример. По распределению
требуется вычислить среднее квадратическое отклонение. Решение.
Среднее квадратическое отклонение суммы взаимно независимых случайных величин равно
Доказательство. Дисперсия суммы случайных величин равна
Тогда
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых одинаково распределенных случайных величин Х1, Х2,…, Хn. Для них среднее арифметическое равно
Докажем три положения [4]: 1. Математическое ожидание среднего арифметического n взаимно независимых одинаково распределенных случайных величин равно математическому ожиданию а каждой из величин
Доказательство:
2. Дисперсия среднего арифметического n взаимно независимых одинаково распределенных случайных величин в n раз меньше дисперсии D каждой из величин:
Доказательство: Так как постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат, то
3. Моменты (начальные, центральные) дискретной случайной величины
Начальный момент порядка r – это математическое ожидание случайной величины Хr
Например, начальные моменты первого и второго порядков равны ν1=M(X); ν 2=M(X2). Центральный момент порядка r задается формулой
при этом Центральный момент второго порядка представляет собой дисперсию. Между начальными и центральными моментами существуют соотношения
Следовательно, формула для вычисления дисперсии может быть записана в виде Законы распределения случайных величин Гипергеометрическое распределение
В партии из N изделий М стандартных (М<N). Из партии отбирают n изделий (без возврата). Случайная величина m – число стандартных изделий среди n отобранных имеет гипергеометрическое распределение. Оно широко используется в статистических методах контроля качества продукции. Биномиальный закон Если в гипергеометрическом распределении объем партии изделий увеличивать, то гипергеометрическое распределение будет приближаться к биномиальному закону (М/N=р)
Здесь выборка – с возвращением! Закон Пуассона Следует из биномиального при n→∞ и малой вероятности р (величина np – постоянная)
где np – среднее. При 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. .
.
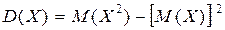 .
.
 .
.
 ,
, .
.
 .
. .
. та же, что и случайной величины Х.
та же, что и случайной величины Х.
 .
. .
. .
. .
. .
. .
. .
. .
. (следует из п.2), т.е. среднее арифметическое n взаимно независимых одинаково распределенных случайных величин имеет значительно меньшее рассеяние (в
(следует из п.2), т.е. среднее арифметическое n взаимно независимых одинаково распределенных случайных величин имеет значительно меньшее рассеяние (в 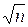 раз), чем каждая отдельная величина
раз), чем каждая отдельная величина .
. ,
, .
.
 .
. .
. .
. ,
, и q (или р) ≤ 0,1 закон Пуассона можно использовать вместо гипергеометрического.
и q (или р) ≤ 0,1 закон Пуассона можно использовать вместо гипергеометрического.