
|
|
Оказывается, что число, которое ближе всего (в смысле критерия наименьших квадратов) к заданной совокупности значений, является средней арифметической этих значений.Числовые характеристики, используемые для описания моделей. Числовые характеристики рядов распределения Для статистического распределения вводится среднее арифметическое наблюдённых значений
Если отдельные варианты повторяются
Между математическим ожиданием и средним арифметическим существует соответствие, аналогичное соответствию между частотой и вероятностью. При увеличении числа опытов среднее арифметическое полученных при наблюдении значений случайной величины приближается к её математическому ожиданию. Статистическая дисперсия
В статистике для характеристики колебаний пользуются величиной, которая называется – абсолютным отклонением
Чаще всего рассеяние характеризуют средним квадратическим отклонением
Для рядов среднее квадратическое отклонение определяется как взвешенный показатель
Значения математического ожидания и дисперсии недостаточно для более полной характеристики случайного распределения. Например, может оказаться, что математические ожидания и дисперсии совпадают, а законы распределения, тем не менее, различны. В этом случае говорят о различной асимметрии. Асимметрию характеризуют при помощи третьего центрального момента
где
Характеристику называют коэффициентом асимметрии. Асимметрия может быть положительной Кривые распределения могут иметь разную крутизну. Для характеристики островершинности или плосковершинности применяют четвёртый центральный момент. С его помощью определяется эксцесс распределения
Для наиболее распространенного в природе нормального распределения эксцесс принимается равным нулю. Все другие распределения характеризуются определённым эксцессом по отношению к нормальному. Величина Свойства статистических параметров 1. Если все частоты (веса) умножить на одно и тоже число, то Так если в формулах
все веса
и аналогично для Отсюда следует, что вычисляя
2.Если варианты признака умножить на одно и тоже число, то Доказательство. Рассмотрим новы варианты
И новое среднее квадратическое отклонение
3. Если по всем вариантам прибавить одно и тоже число
но
Следовательно
Далее получаем
Дисперсия равна среднему квадрату минус квадрат средней
И для взвешенных показателей
Для первой формулы имеем
вынесем
Аналогично доказывается и для взвешенных показателей. Свойства средней арифметической Свойство1. Сумма отклонений от средней арифметической равна нулю. Запишем
но
следовательно
Свойство2.
Сумма квадратов отклонений от средней арифметической меньше, чем сумма квадратов отклонений от любого другого числа. Обозначим через сумму квадратов отклонений вариантов от числа и найдем значение числа
Необходимое условие минимума
Дифференцируя, имеем
Заметим, что строго говоря , кроме условия
Это условие, очевидно удовлетворяется, так как
Смысл критерия наименьших квадратов заключается в следующем. Отыскиваем число Оказывается, что число, которое ближе всего (в смысле критерия наименьших квадратов) к заданной совокупности значений, является средней арифметической этих значений. Минимальное свойство характеризует связь между средней арифметической и средним квадратическим отклонением. Среднее квадратическое отклонение, вычисленное от средней арифметической, оказывается меньше, чем вычисленное от какой либо другой величины (например медианы или моды)
если
Наконец, заметим, что начальные и центральные моменты любых порядков для статистического распределения вычисляются по формулам
При увеличении объёма экспериментальных данных все статистические характеристики, очевидно, будут сходиться по вероятностям к соответствующим математическим характеристикам. Любая статистическая характеристика содержит элемент случайности. При большом количестве наблюдений эта случайность сглаживается. Увеличения числа опытов не всегда возможно, поэтому приходится применять косвенные методы. Задача подбора теоретической кривой распределения носит название задачи выравнивания рядов распределения.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 - частота вариантов
- частота вариантов  . Формула даёт значение взвешенной средней арифметической, и числа
. Формула даёт значение взвешенной средней арифметической, и числа  (в теории вероятностей
(в теории вероятностей  )
)

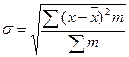
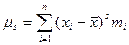
 =3. Для симметричных распределений все нечётные центральные моменты равны нулю. Поэтому естественно принять в качестве характеристики асимметрии, какой либо из них. Обычно используется третий. Для того чтобы характеристика была безразмерной,
=3. Для симметричных распределений все нечётные центральные моменты равны нулю. Поэтому естественно принять в качестве характеристики асимметрии, какой либо из них. Обычно используется третий. Для того чтобы характеристика была безразмерной,  делят на среднее квадратическое отклонение в третьей степени
делят на среднее квадратическое отклонение в третьей степени
 и отрицательной
и отрицательной  .
.
 для нормального закона равна 3. Поэтому в общей формуле, в правой части вычитается 3. Кривые, более островершинные по сравнению с нормальной обладают положительным эксцессом, более плосковершинные – отрицательным.
для нормального закона равна 3. Поэтому в общей формуле, в правой части вычитается 3. Кривые, более островершинные по сравнению с нормальной обладают положительным эксцессом, более плосковершинные – отрицательным. и
и  не изменяются
не изменяются ; и
; и  , то
, то =
=  =
= 
 , где
, где  =
=  =
=  =
= 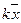
 =
=  =
=  =
= 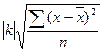 =
= 
 , то
, то  =
=  +
+  .
. ,
, 

 =
=  =
=  =
= 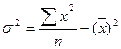


 -
-  +
+ 
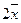 за знак суммы, и учитывая, что
за знак суммы, и учитывая, что 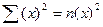 , получим
, получим -
-  +
+  =
=  =
= 
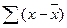 =
=  -
- 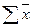
 , так как
, так как 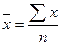 и
и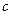
 минимальна.
минимальна.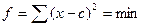 (называется - критерий наименьших квадратов)
(называется - критерий наименьших квадратов)
 , или
, или 
 тогда
тогда  ,
,  , откуда
, откуда

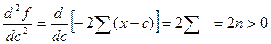
 . А поскольку есть целый ряд значений
. А поскольку есть целый ряд значений 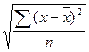


 .
.
