
|
|
Дисперсия суммы случайных величинФункции случайных аргументов
Для решения многих задач необходимо определение характеристик функции по известным характеристикам аргументов (случайных величин) или определение закона распределения функции случайных величин по известному закону аргумента.
Математическое ожидание суммы случайных величин Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин. Постановка задачи. Дана система случайных величин (X,Y), плотность распределения которой Используя определение математического ожидания случайной непрерывной величины, получаем
Если случайная величина Эта теорема справедлива как для зависимых, так и для независимых величин. Математическое ожидание линейной функции случайных величинравно той же линейной функции от математических ожиданий этих величин:
В случае комплексного характера случайной величины
Математическое ожидание произведениянескольких независимых случайных величин равно произведению математических ожиданий этих случайных величин. Постановка задачи. Пусть случайная величина
Поскольку случайные величины
Тогда математическое ожидание случайной величины Z будет равно
Выражение (4.2) не применимо для зависимых случайных величин. Математическое ожидание произведения двух зависимых случайных величин равно сумме произведений их математических ожиданий и корреляционного момента:
Справедливость этого свойства вытекает из формулы корреляционного момента. Математическое ожидание нелинейной функции случайных аргументов.Пусть случайная величина Z является функцией случайных аргументов Поставленная задача решается точно только для некоторых частных случаев. В общем случае при решении этой задачи сначала нелинейную функцию в окрестности точки
учитывая, что Таким образом, МО нелинейной функции случайных аргументов равно этой же функции от математических ожиданий этих аргументов.
Дисперсия суммы случайных величин Дисперсия суммы двух случайных величин равна сумме дисперсий и удвоенного корреляционного момента этих величин:
Доказательство. Пусть X+Y=Z, тогда
что и требовалось доказать. Формула (4.2) может быть обобщена на любое число слагаемых:
где Если случайные величины
Справедливость равенства (4.7) вытекает из того, что для не коррелированных случайных величин корреляционный момент Дисперсия линейной функции случайных величинравна
где Если случайные величины
Пример. Определить дисперсию случайной величины Дисперсией случайной комплексной величины называют МО квадрата модуля комплексной центрированной случайной величины, поэтому
Дисперсия произведениядвух независимых случайных величин X и Y вычисляется по формуле
Доказательство. Пусть
Так как случайные величины X и Y независимы, то
Кроме того, Следовательно,
что и требовалось доказать. Дисперсия нелинейной функции случайных аргументов.Пусть случайная величина Z является функцией случайных аргументов В общем случае при решении этой задачи нелинейную функцию в окрестности точки

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 известна. Требуется определить математическое ожидание суммы случайных величин M(Z)=M(X+Y).
известна. Требуется определить математическое ожидание суммы случайных величин M(Z)=M(X+Y).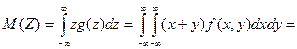

 Т.е.
Т.е.  .
.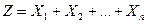 , то
, то  . (4.1)
. (4.1) , где
, где  - неслучайные величины.
- неслучайные величины. математическое ожиданиеее также будет комплексным:
математическое ожиданиеее также будет комплексным: .
. имеет закон распределения
имеет закон распределения  . Требуется определить МО M(Z) случайной величины Z.
. Требуется определить МО M(Z) случайной величины Z.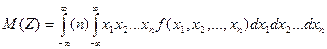 .
. являются независимыми, то функцию
являются независимыми, то функцию 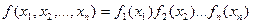 .
. . Откуда
. Откуда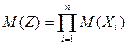 . (4.2)
. (4.2) . (4.3)
. (4.3)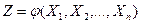 . Требуется определить МО M(Z).
. Требуется определить МО M(Z). линеаризуют разложением ее в ряд Тейлора:
линеаризуют разложением ее в ряд Тейлора: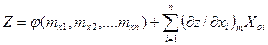 . Применяя к этой случайной величине свойство МО линейной функции, находим:
. Применяя к этой случайной величине свойство МО линейной функции, находим: , (4.4)
, (4.4) .
.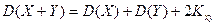 . (4.5)
. (4.5)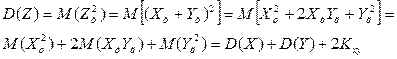 ,
, , (4.6)
, (4.6) - корреляционный момент случайных величин
- корреляционный момент случайных величин  , знак
, знак 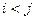 под суммой обозначает, что суммирование распространяется на все возможные парные сочетания случайных величин
под суммой обозначает, что суммирование распространяется на все возможные парные сочетания случайных величин  . (4.7)
. (4.7) .
. , (4.8)
, (4.8) . (4.9)
. (4.9) . Следовательно, дисперсия комплексной случайной величины равна сумме дисперсий действительной X и мнимой Y случайных частей.
. Следовательно, дисперсия комплексной случайной величины равна сумме дисперсий действительной X и мнимой Y случайных частей.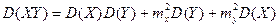 . (4.10)
. (4.10)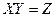 , тогда
, тогда .
. и
и  также будут независимы, поэтому
также будут независимы, поэтому .
. .
. ,
, . (4.11)
. (4.11)